2020年秋沪科版八年级数学上册第15章轴对称与等腰三角形单元测试卷(word含答案)
文档属性
| 名称 | 2020年秋沪科版八年级数学上册第15章轴对称与等腰三角形单元测试卷(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 499.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 07:12:24 | ||
图片预览




文档简介
2020年秋沪科版八年级数学上册第15章轴对称与等腰三角形单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形中,不是轴对称图形的是
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是
A.AB=2BD
B.AD⊥BC
C.AD平分∠BAC
D.∠B=∠C
3.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N.若ON=8
cm,则OM的长为
A.4
cm
B.5
cm
C.8
cm
D.16
cm
4.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最小边BC=3
cm,则最长边AB的长为
A.9
cm
B.8
cm
C.7
cm
D.6
cm
5.如图,在△ABC中,边AC的垂直平分线交边AB于点D,连接CD.若∠A=60°,则∠BDC的大小为
A.90°
B.100°
C.120°
D.130°
6.如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有
A.5个
B.6个
C.7个
D.8个
7.在△ABC中,∠ABC与∠ACB的平分线交于点I,过点I作DE∥BC交AB于点D,交AC于点E,AB=5,AC=3,∠A=50°,则下列说法错误的是
A.△DBI和△EIC是等腰三角形
B.∠BIC=115°
C.△ADE的周长是8
D.I为DE的中点
8.如图,在△ABC中,AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB.若BE=5
cm,CE=3
cm,则△CDE的周长是
A.15
cm
B.13
cm
C.11
cm
D.9
cm
9.如图,在平面直角坐标系中,已知点A(1,1),B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为
A.(0,1)
B.(0,2)
C.
D.(2,0)
10.如图,△PAB与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°;②AD∥BC;③PC⊥AB;④四边形ABCD是轴对称图形.其中正确的个数为
A.4
B.3
C.2
D.1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若一个等腰三角形的顶角等于50°,则它的底角等于 .?
12.如图,点O在△ABC内,且到三边的距离相等.若∠A=60°,则∠BOC= .?
13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF= .?
14.如果两个等腰三角形的腰长相等、面积也相等,那么我们把这两个等腰三角形称为一对合同三角形.已知一对合同三角形的底角分别为x°和y°,则y= .(用含x的代数式表示)?
三、解答题(本大题共6小题,满分60分)
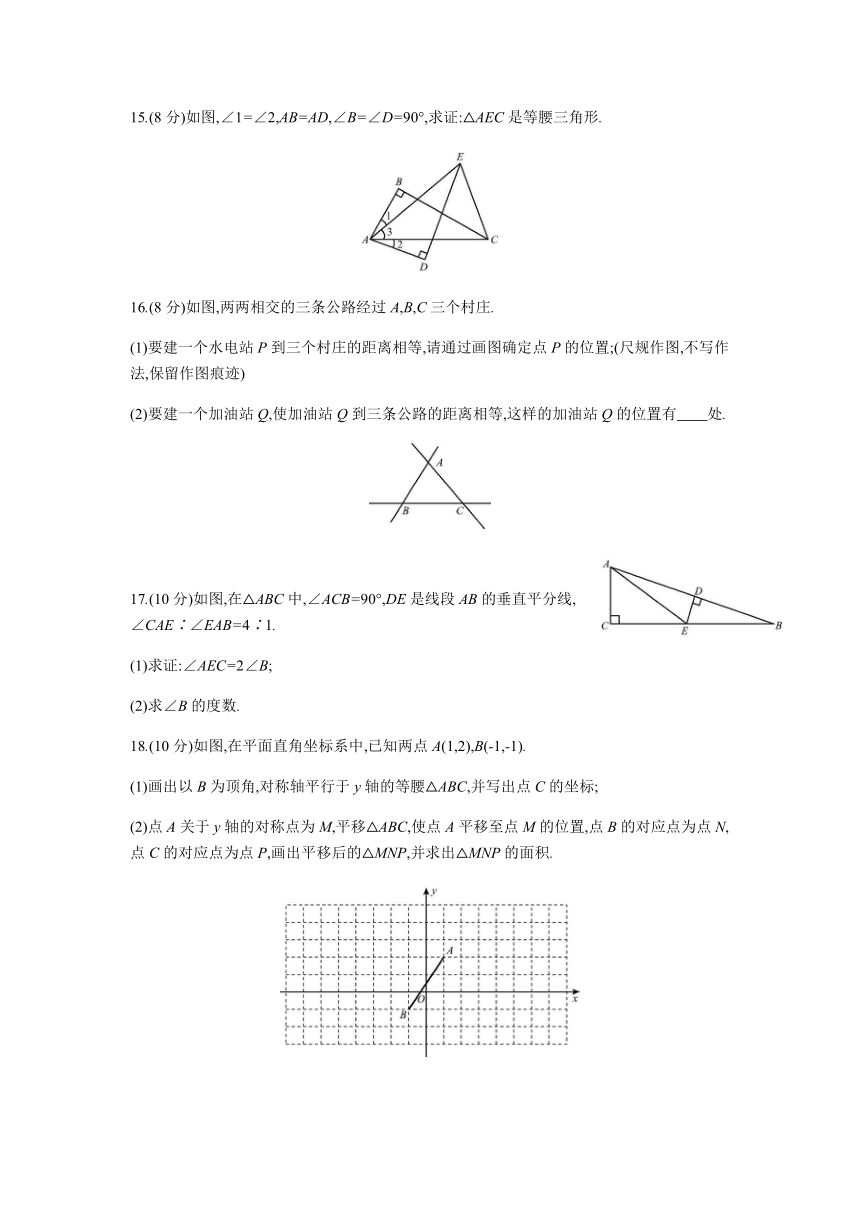
15.(8分)如图,∠1=∠2,AB=AD,∠B=∠D=90°,求证:△AEC是等腰三角形.
16.(8分)如图,两两相交的三条公路经过A,B,C三个村庄.
(1)要建一个水电站P到三个村庄的距离相等,请通过画图确定点P的位置;(尺规作图,不写作法,保留作图痕迹)
(2)要建一个加油站Q,使加油站Q到三条公路的距离相等,这样的加油站Q的位置有 处.?
17.(10分)如图,在△ABC中,∠ACB=90°,DE是线段AB的垂直平分线,∠CAE∶∠EAB=4∶1.
(1)求证:∠AEC=2∠B;
(2)求∠B的度数.
18.(10分)如图,在平面直角坐标系中,已知两点A(1,2),B(-1,-1).
(1)画出以B为顶角,对称轴平行于y轴的等腰△ABC,并写出点C的坐标;
(2)点A关于y轴的对称点为M,平移△ABC,使点A平移至点M的位置,点B的对应点为点N,点C的对应点为点P,画出平移后的△MNP,并求出△MNP的面积.
19.(12分)如图,已知D是BC的中点,过点D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=10,AC=6,求线段CG的长.
20.(12分)问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D= .?
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D= .这两个图中,∠D与∠A度数的比是 .?
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.
2020年秋沪科版八年级数学上册第15章轴对称与等腰三角形单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形中,不是轴对称图形的是
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是
A.AB=2BD
B.AD⊥BC
C.AD平分∠BAC
D.∠B=∠C
3.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N.若ON=8
cm,则OM的长为
A.4
cm
B.5
cm
C.8
cm
D.16
cm
4.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最小边BC=3
cm,则最长边AB的长为
A.9
cm
B.8
cm
C.7
cm
D.6
cm
5.如图,在△ABC中,边AC的垂直平分线交边AB于点D,连接CD.若∠A=60°,则∠BDC的大小为
A.90°
B.100°
C.120°
D.130°
6.如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有
A.5个
B.6个
C.7个
D.8个
7.在△ABC中,∠ABC与∠ACB的平分线交于点I,过点I作DE∥BC交AB于点D,交AC于点E,AB=5,AC=3,∠A=50°,则下列说法错误的是
A.△DBI和△EIC是等腰三角形
B.∠BIC=115°
C.△ADE的周长是8
D.I为DE的中点
8.如图,在△ABC中,AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB.若BE=5
cm,CE=3
cm,则△CDE的周长是
A.15
cm
B.13
cm
C.11
cm
D.9
cm
9.如图,在平面直角坐标系中,已知点A(1,1),B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为
A.(0,1)
B.(0,2)
C.
D.(2,0)
10.如图,△PAB与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°;②AD∥BC;③PC⊥AB;④四边形ABCD是轴对称图形.其中正确的个数为
A.4
B.3
C.2
D.1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若一个等腰三角形的顶角等于50°,则它的底角等于 65° .?
12.如图,点O在△ABC内,且到三边的距离相等.若∠A=60°,则∠BOC= 120° .?
13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF= 2 .?
14.如果两个等腰三角形的腰长相等、面积也相等,那么我们把这两个等腰三角形称为一对合同三角形.已知一对合同三角形的底角分别为x°和y°,则y= x或90-x .(用含x的代数式表示)?
三、解答题(本大题共6小题,满分60分)
15.(8分)如图,∠1=∠2,AB=AD,∠B=∠D=90°,求证:△AEC是等腰三角形.
证明:∵∠1=∠2,∴∠1+∠3=∠2+∠3,即∠BAC=∠DAE,又∵AB=AD,∠B=∠D,
∴△ABC≌△ADE(ASA),∴AC=AE,∴△AEC是等腰三角形.
16.(8分)如图,两两相交的三条公路经过A,B,C三个村庄.
(1)要建一个水电站P到三个村庄的距离相等,请通过画图确定点P的位置;(尺规作图,不写作法,保留作图痕迹)
(2)要建一个加油站Q,使加油站Q到三条公路的距离相等,这样的加油站Q的位置有 4 处.?
解:(1)略.
17.(10分)如图,在△ABC中,∠ACB=90°,DE是线段AB的垂直平分线,∠CAE∶∠EAB=4∶1.
(1)求证:∠AEC=2∠B;
(2)求∠B的度数.
解:(1)∵DE是线段AB的垂直平分线,∴AE=BE.
∴∠B=∠EAD,∴∠AEC=∠B+∠EAD=2∠B.
(2)设∠B=x°,∴∠CAE=4x°,
∴4x+x+x+90=180,∴x=15,∴∠B=15°.
18.(10分)如图,在平面直角坐标系中,已知两点A(1,2),B(-1,-1).
(1)画出以B为顶角,对称轴平行于y轴的等腰△ABC,并写出点C的坐标;
(2)点A关于y轴的对称点为M,平移△ABC,使点A平移至点M的位置,点B的对应点为点N,点C的对应点为点P,画出平移后的△MNP,并求出△MNP的面积.
解:(1)图略,C(-3,2).
(2)图略,△MNP的面积=×4×3=6.
19.(12分)如图,已知D是BC的中点,过点D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=10,AC=6,求线段CG的长.
解:(1)连接EC,EB.
∵AE是∠CAB的平分线,EF⊥AB于点F,EG⊥AC于点G,∴EF=EG.
∵点D是BC的中点,ED⊥BC,∴ED垂直平分BC,∴EC=EB,
∴Rt△CGE≌Rt△BFE(HL),∴BF=CG.
(2)CG=2.
20.(12分)问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D= 30° .?
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D= 50° .这两个图中,∠D与∠A度数的比是 1∶2 .?
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.
解:(2)成立.
理由:如题图1,在△ABC中,∠ACE=∠A+∠ABC,
在△DBC中,∠DCE=∠D+∠DBC,
①
∵CD平分∠ACE,BD平分∠ABC,∴∠ACE=2∠DCE,∠ABC=2∠DBC,
∴2∠DCE=∠A+2∠DBC,
②
由①×2-②,得2∠D+2∠DBC-(∠A+2∠DBC)=0,
∴∠A=2∠D.
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形中,不是轴对称图形的是
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是
A.AB=2BD
B.AD⊥BC
C.AD平分∠BAC
D.∠B=∠C
3.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N.若ON=8
cm,则OM的长为
A.4
cm
B.5
cm
C.8
cm
D.16
cm
4.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最小边BC=3
cm,则最长边AB的长为
A.9
cm
B.8
cm
C.7
cm
D.6
cm
5.如图,在△ABC中,边AC的垂直平分线交边AB于点D,连接CD.若∠A=60°,则∠BDC的大小为
A.90°
B.100°
C.120°
D.130°
6.如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有
A.5个
B.6个
C.7个
D.8个
7.在△ABC中,∠ABC与∠ACB的平分线交于点I,过点I作DE∥BC交AB于点D,交AC于点E,AB=5,AC=3,∠A=50°,则下列说法错误的是
A.△DBI和△EIC是等腰三角形
B.∠BIC=115°
C.△ADE的周长是8
D.I为DE的中点
8.如图,在△ABC中,AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB.若BE=5
cm,CE=3
cm,则△CDE的周长是
A.15
cm
B.13
cm
C.11
cm
D.9
cm
9.如图,在平面直角坐标系中,已知点A(1,1),B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为
A.(0,1)
B.(0,2)
C.
D.(2,0)
10.如图,△PAB与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°;②AD∥BC;③PC⊥AB;④四边形ABCD是轴对称图形.其中正确的个数为
A.4
B.3
C.2
D.1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若一个等腰三角形的顶角等于50°,则它的底角等于 .?
12.如图,点O在△ABC内,且到三边的距离相等.若∠A=60°,则∠BOC= .?
13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF= .?
14.如果两个等腰三角形的腰长相等、面积也相等,那么我们把这两个等腰三角形称为一对合同三角形.已知一对合同三角形的底角分别为x°和y°,则y= .(用含x的代数式表示)?
三、解答题(本大题共6小题,满分60分)
15.(8分)如图,∠1=∠2,AB=AD,∠B=∠D=90°,求证:△AEC是等腰三角形.
16.(8分)如图,两两相交的三条公路经过A,B,C三个村庄.
(1)要建一个水电站P到三个村庄的距离相等,请通过画图确定点P的位置;(尺规作图,不写作法,保留作图痕迹)
(2)要建一个加油站Q,使加油站Q到三条公路的距离相等,这样的加油站Q的位置有 处.?
17.(10分)如图,在△ABC中,∠ACB=90°,DE是线段AB的垂直平分线,∠CAE∶∠EAB=4∶1.
(1)求证:∠AEC=2∠B;
(2)求∠B的度数.
18.(10分)如图,在平面直角坐标系中,已知两点A(1,2),B(-1,-1).
(1)画出以B为顶角,对称轴平行于y轴的等腰△ABC,并写出点C的坐标;
(2)点A关于y轴的对称点为M,平移△ABC,使点A平移至点M的位置,点B的对应点为点N,点C的对应点为点P,画出平移后的△MNP,并求出△MNP的面积.
19.(12分)如图,已知D是BC的中点,过点D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=10,AC=6,求线段CG的长.
20.(12分)问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D= .?
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D= .这两个图中,∠D与∠A度数的比是 .?
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.
2020年秋沪科版八年级数学上册第15章轴对称与等腰三角形单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形中,不是轴对称图形的是
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是
A.AB=2BD
B.AD⊥BC
C.AD平分∠BAC
D.∠B=∠C
3.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N.若ON=8
cm,则OM的长为
A.4
cm
B.5
cm
C.8
cm
D.16
cm
4.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最小边BC=3
cm,则最长边AB的长为
A.9
cm
B.8
cm
C.7
cm
D.6
cm
5.如图,在△ABC中,边AC的垂直平分线交边AB于点D,连接CD.若∠A=60°,则∠BDC的大小为
A.90°
B.100°
C.120°
D.130°
6.如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有
A.5个
B.6个
C.7个
D.8个
7.在△ABC中,∠ABC与∠ACB的平分线交于点I,过点I作DE∥BC交AB于点D,交AC于点E,AB=5,AC=3,∠A=50°,则下列说法错误的是
A.△DBI和△EIC是等腰三角形
B.∠BIC=115°
C.△ADE的周长是8
D.I为DE的中点
8.如图,在△ABC中,AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB.若BE=5
cm,CE=3
cm,则△CDE的周长是
A.15
cm
B.13
cm
C.11
cm
D.9
cm
9.如图,在平面直角坐标系中,已知点A(1,1),B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为
A.(0,1)
B.(0,2)
C.
D.(2,0)
10.如图,△PAB与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°;②AD∥BC;③PC⊥AB;④四边形ABCD是轴对称图形.其中正确的个数为
A.4
B.3
C.2
D.1
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若一个等腰三角形的顶角等于50°,则它的底角等于 65° .?
12.如图,点O在△ABC内,且到三边的距离相等.若∠A=60°,则∠BOC= 120° .?
13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF= 2 .?
14.如果两个等腰三角形的腰长相等、面积也相等,那么我们把这两个等腰三角形称为一对合同三角形.已知一对合同三角形的底角分别为x°和y°,则y= x或90-x .(用含x的代数式表示)?
三、解答题(本大题共6小题,满分60分)
15.(8分)如图,∠1=∠2,AB=AD,∠B=∠D=90°,求证:△AEC是等腰三角形.
证明:∵∠1=∠2,∴∠1+∠3=∠2+∠3,即∠BAC=∠DAE,又∵AB=AD,∠B=∠D,
∴△ABC≌△ADE(ASA),∴AC=AE,∴△AEC是等腰三角形.
16.(8分)如图,两两相交的三条公路经过A,B,C三个村庄.
(1)要建一个水电站P到三个村庄的距离相等,请通过画图确定点P的位置;(尺规作图,不写作法,保留作图痕迹)
(2)要建一个加油站Q,使加油站Q到三条公路的距离相等,这样的加油站Q的位置有 4 处.?
解:(1)略.
17.(10分)如图,在△ABC中,∠ACB=90°,DE是线段AB的垂直平分线,∠CAE∶∠EAB=4∶1.
(1)求证:∠AEC=2∠B;
(2)求∠B的度数.
解:(1)∵DE是线段AB的垂直平分线,∴AE=BE.
∴∠B=∠EAD,∴∠AEC=∠B+∠EAD=2∠B.
(2)设∠B=x°,∴∠CAE=4x°,
∴4x+x+x+90=180,∴x=15,∴∠B=15°.
18.(10分)如图,在平面直角坐标系中,已知两点A(1,2),B(-1,-1).
(1)画出以B为顶角,对称轴平行于y轴的等腰△ABC,并写出点C的坐标;
(2)点A关于y轴的对称点为M,平移△ABC,使点A平移至点M的位置,点B的对应点为点N,点C的对应点为点P,画出平移后的△MNP,并求出△MNP的面积.
解:(1)图略,C(-3,2).
(2)图略,△MNP的面积=×4×3=6.
19.(12分)如图,已知D是BC的中点,过点D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=10,AC=6,求线段CG的长.
解:(1)连接EC,EB.
∵AE是∠CAB的平分线,EF⊥AB于点F,EG⊥AC于点G,∴EF=EG.
∵点D是BC的中点,ED⊥BC,∴ED垂直平分BC,∴EC=EB,
∴Rt△CGE≌Rt△BFE(HL),∴BF=CG.
(2)CG=2.
20.(12分)问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D= 30° .?
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D= 50° .这两个图中,∠D与∠A度数的比是 1∶2 .?
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.
解:(2)成立.
理由:如题图1,在△ABC中,∠ACE=∠A+∠ABC,
在△DBC中,∠DCE=∠D+∠DBC,
①
∵CD平分∠ACE,BD平分∠ABC,∴∠ACE=2∠DCE,∠ABC=2∠DBC,
∴2∠DCE=∠A+2∠DBC,
②
由①×2-②,得2∠D+2∠DBC-(∠A+2∠DBC)=0,
∴∠A=2∠D.
