2020年秋沪科版八年级数学上册第14章全等三角形单元测试卷(word含答案)
文档属性
| 名称 | 2020年秋沪科版八年级数学上册第14章全等三角形单元测试卷(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 368.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 07:16:15 | ||
图片预览



文档简介
2020年秋沪科版八年级数学上册第14章全等三角形单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列物品不是利用三角形稳定性的是
A.自行车的三角形车架
B.三角形房架
C.照相机的三脚架
D.放缩尺
2.如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠3=∠4
3.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是
A.76°
B.62°
C.42°
D.76°,62°或42°都可以
4.如图,AC⊥BD于点P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有
A.0个
B.1个
C.2个
D.3个
5.下列选项中,能使两个直角三角形全等的是
A.一组锐角对应相等
B.两组锐角对应相等
C.一组对边对应相等
D.两组对边对应相等
6.下列说法正确的是
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
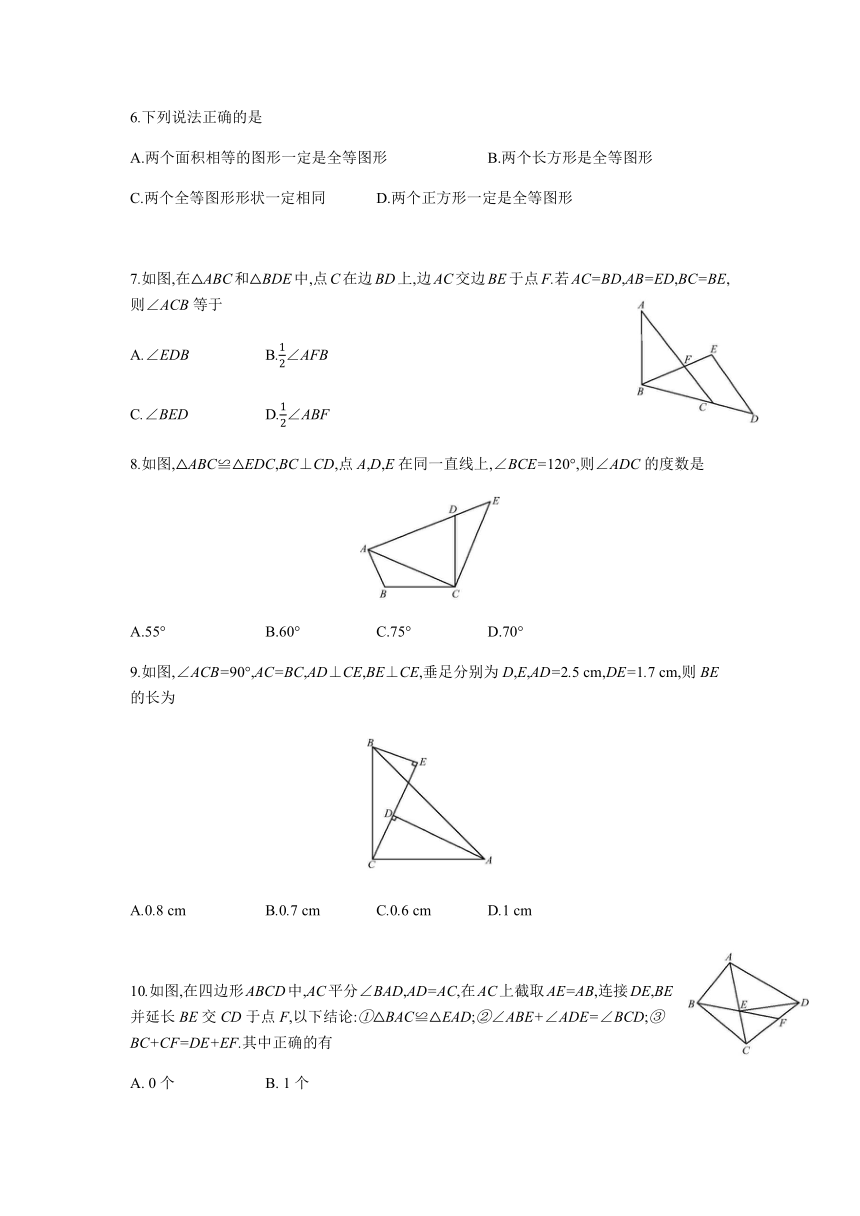
7.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于
A.∠EDB
B.∠AFB
C.∠BED
D.∠ABF
8.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一直线上,∠BCE=120°,则∠ADC的度数是
A.55°
B.60°
C.75°
D.70°
9.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5
cm,DE=1.7
cm,则BE的长为
A.0.8
cm
B.0.7
cm
C.0.6
cm
D.1
cm
10.如图,在四边形ABCD中,AC平分∠BAD,AD=AC,在AC上截取AE=AB,连接DE,BE,并延长BE交CD于点F,以下结论:①△BAC≌△EAD;②∠ABE+∠ADE=∠BCD;③BC+CF=DE+EF.其中正确的有
A.
0个
B.
1个
C.
2个
D.
3个
二、填空题(本大题共4小题,每小题5分,满分20分)
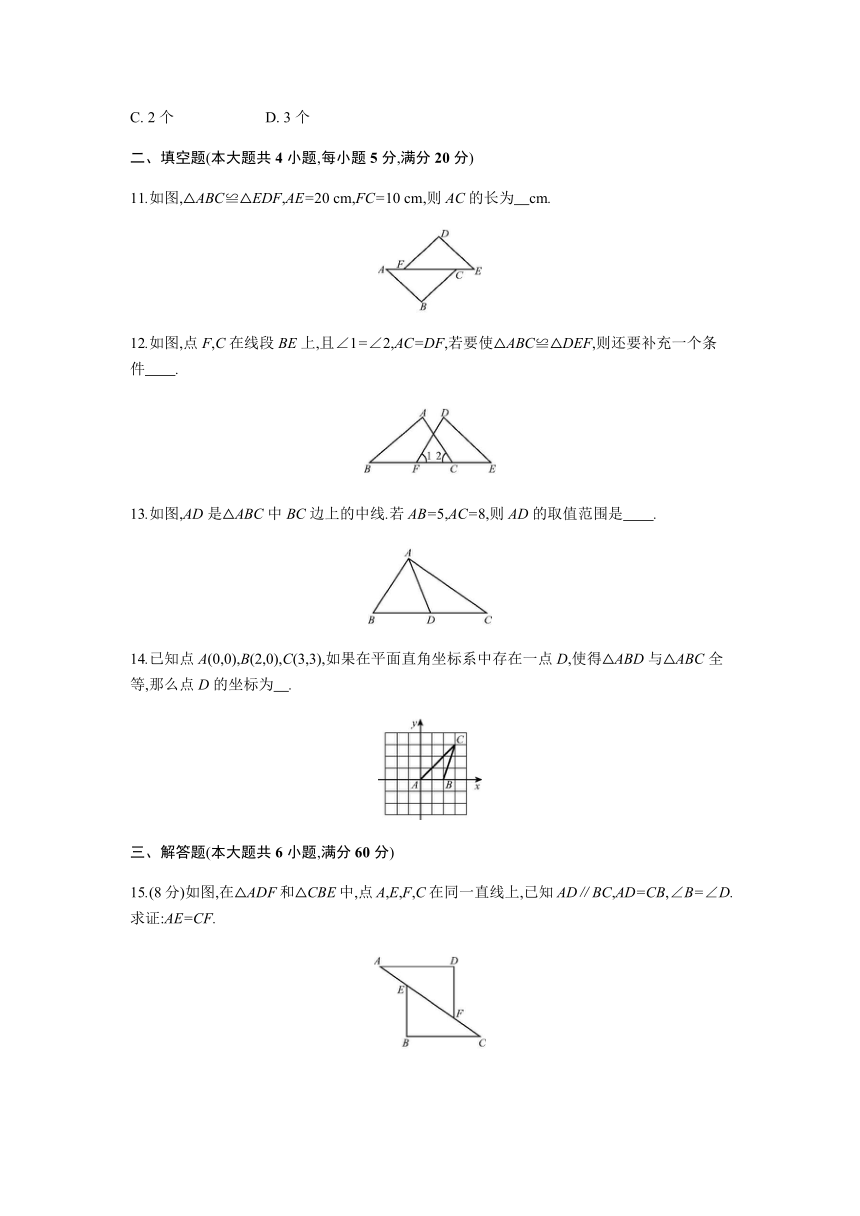
11.如图,△ABC≌△EDF,AE=20
cm,FC=10
cm,则AC的长为 cm.?
12.如图,点F,C在线段BE上,且∠1=∠2,AC=DF,若要使△ABC≌△DEF,则还要补充一个条件 .?
13.如图,AD是△ABC中BC边上的中线.若AB=5,AC=8,则AD的取值范围是 .?
14.已知点A(0,0),B(2,0),C(3,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为 .?
三、解答题(本大题共6小题,满分60分)
15.(8分)如图,在△ADF和△CBE中,点A,E,F,C在同一直线上,已知AD∥BC,AD=CB,∠B=∠D.求证:AE=CF.
16.(8分)在Rt△ABC中,∠ACB=90°,BC=2
cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5
cm,求AE的长.
17.(10分)小明家所在的小区有一个池塘,如图,A,B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在BD的中点C处有一个雕塑,小明从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A,B两点之间的距离.
(1)你能说明小明这样做的根据吗?
(2)如果小明未带测量工具,但是知道A和假山、雕塑分别相距200米、120米,你能帮助他确定AB的长度范围吗?
18.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=48°,求∠BDE的度数.
19.(12分)如图,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,CE与BF相交于点M.
求证:(1)EC=BF;
(2)EC⊥BF.
20.(12分)已知∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1,①线段CD和BE的数量关系是 ;?
②请写出线段AD,BE,DE之间的数量关系并证明.
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系.
2020年秋沪科版八年级数学上册第14章全等三角形单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列物品不是利用三角形稳定性的是
A.自行车的三角形车架
B.三角形房架
C.照相机的三脚架
D.放缩尺
2.如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠3=∠4
3.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是
A.76°
B.62°
C.42°
D.76°,62°或42°都可以
4.如图,AC⊥BD于点P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有
A.0个
B.1个
C.2个
D.3个
5.下列选项中,能使两个直角三角形全等的是
A.一组锐角对应相等
B.两组锐角对应相等
C.一组对边对应相等
D.两组对边对应相等
6.下列说法正确的是
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
7.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于
A.∠EDB
B.∠AFB
C.∠BED
D.∠ABF
8.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一直线上,∠BCE=120°,则∠ADC的度数是
A.55°
B.60°
C.75°
D.70°
9.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5
cm,DE=1.7
cm,则BE的长为
A.0.8
cm
B.0.7
cm
C.0.6
cm
D.1
cm
10.如图,在四边形ABCD中,AC平分∠BAD,AD=AC,在AC上截取AE=AB,连接DE,BE,并延长BE交CD于点F,以下结论:①△BAC≌△EAD;②∠ABE+∠ADE=∠BCD;③BC+CF=DE+EF.其中正确的有
A.
0个
B.
1个
C.
2个
D.
3个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,△ABC≌△EDF,AE=20
cm,FC=10
cm,则AC的长为 15 cm.?
12.如图,点F,C在线段BE上,且∠1=∠2,AC=DF,若要使△ABC≌△DEF,则还要补充一个条件 ∠A=∠D(答案不唯一,合理即可) .?
13.如图,AD是△ABC中BC边上的中线.若AB=5,AC=8,则AD的取值范围是 1.514.已知点A(0,0),B(2,0),C(3,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为 (3,-3)或(-1,3)或(-1,-3) .?
三、解答题(本大题共6小题,满分60分)
15.(8分)如图,在△ADF和△CBE中,点A,E,F,C在同一直线上,已知AD∥BC,AD=CB,∠B=∠D.求证:AE=CF.
证明:∵AD∥BC,∴∠A=∠C,在△ADF和△CBE中,
∴△ADF≌△CBE,∴AF=CE,∴AE=CF.
16.(8分)在Rt△ABC中,∠ACB=90°,BC=2
cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5
cm,求AE的长.
解:∵EF⊥AC,∴∠FEC=90°.∵∠ACB=90°,∴∠ACB=∠FEC,∠ECF+∠BCD=90°,∵CD⊥AB,∴∠BCD+∠B=90°,∴∠ECF=∠B.
在△ABC和△FCE中,∴△FCE≌△ABC(ASA),∴EF=AC.
∵BC=2
cm,EF=5
cm,∴AE=AC-CE=5-2=3
cm.
17.(10分)小明家所在的小区有一个池塘,如图,A,B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在BD的中点C处有一个雕塑,小明从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A,B两点之间的距离.
(1)你能说明小明这样做的根据吗?
(2)如果小明未带测量工具,但是知道A和假山、雕塑分别相距200米、120米,你能帮助他确定AB的长度范围吗?
解:(1)在△ACB和△ECD中,∴△ACB≌△ECD(SAS),∴DE=AB.
(2)连接AD.
∵AD=200米,AC=120米,∴AE=240米,∴40米18.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=48°,求∠BDE的度数.
解:(1)∵∠A=∠B,∠BOE=∠AOD,∴∠2=∠BEA,∵∠1=∠2,∴∠BEA=∠1.
∴∠BEA+∠AED=∠1+∠AED,即∠BED=∠AEC,
在△AEC和△BED中,∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,∴EC=ED,∠C=∠BDE,∴∠C=∠EDC,
∵∠1=48°,∴∠C=∠EDC=66°,∴∠BDE=66°.
19.(12分)如图,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,CE与BF相交于点M.
求证:(1)EC=BF;
(2)EC⊥BF.
证明:(1)∵AE⊥AB,AF⊥AC,∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF.
在△EAC和△BAF中,∴△EAC≌△BAF(SAS),∴EC=BF.
(2)∵△EAC≌△BAF,∴∠AEC=∠ABF,又∵∠AEB+∠ABE=90°,
∴∠CEB+∠ABF+∠EBA=90°,∴∠MEB+∠EBM=90°,即∠EMB=90°,∴EC⊥BF.
20.(12分)已知∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1,①线段CD和BE的数量关系是 CD=BE ;?
②请写出线段AD,BE,DE之间的数量关系并证明.
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系.
解:(1)②AD=BE+DE.
理由:∵∠ACB=90°,AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠B=90°,∴∠ACD=∠B.
在△ACD和△CBE中,∴△ACD≌△CBE,∴AD=CE,CD=BE,
∵CE=CD+DE=BE+DE,∴AD=BE+DE.
(2)②中的结论不成立,DE=AD+BE.
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列物品不是利用三角形稳定性的是
A.自行车的三角形车架
B.三角形房架
C.照相机的三脚架
D.放缩尺
2.如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠3=∠4
3.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是
A.76°
B.62°
C.42°
D.76°,62°或42°都可以
4.如图,AC⊥BD于点P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有
A.0个
B.1个
C.2个
D.3个
5.下列选项中,能使两个直角三角形全等的是
A.一组锐角对应相等
B.两组锐角对应相等
C.一组对边对应相等
D.两组对边对应相等
6.下列说法正确的是
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
7.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于
A.∠EDB
B.∠AFB
C.∠BED
D.∠ABF
8.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一直线上,∠BCE=120°,则∠ADC的度数是
A.55°
B.60°
C.75°
D.70°
9.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5
cm,DE=1.7
cm,则BE的长为
A.0.8
cm
B.0.7
cm
C.0.6
cm
D.1
cm
10.如图,在四边形ABCD中,AC平分∠BAD,AD=AC,在AC上截取AE=AB,连接DE,BE,并延长BE交CD于点F,以下结论:①△BAC≌△EAD;②∠ABE+∠ADE=∠BCD;③BC+CF=DE+EF.其中正确的有
A.
0个
B.
1个
C.
2个
D.
3个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,△ABC≌△EDF,AE=20
cm,FC=10
cm,则AC的长为 cm.?
12.如图,点F,C在线段BE上,且∠1=∠2,AC=DF,若要使△ABC≌△DEF,则还要补充一个条件 .?
13.如图,AD是△ABC中BC边上的中线.若AB=5,AC=8,则AD的取值范围是 .?
14.已知点A(0,0),B(2,0),C(3,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为 .?
三、解答题(本大题共6小题,满分60分)
15.(8分)如图,在△ADF和△CBE中,点A,E,F,C在同一直线上,已知AD∥BC,AD=CB,∠B=∠D.求证:AE=CF.
16.(8分)在Rt△ABC中,∠ACB=90°,BC=2
cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5
cm,求AE的长.
17.(10分)小明家所在的小区有一个池塘,如图,A,B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在BD的中点C处有一个雕塑,小明从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A,B两点之间的距离.
(1)你能说明小明这样做的根据吗?
(2)如果小明未带测量工具,但是知道A和假山、雕塑分别相距200米、120米,你能帮助他确定AB的长度范围吗?
18.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=48°,求∠BDE的度数.
19.(12分)如图,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,CE与BF相交于点M.
求证:(1)EC=BF;
(2)EC⊥BF.
20.(12分)已知∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1,①线段CD和BE的数量关系是 ;?
②请写出线段AD,BE,DE之间的数量关系并证明.
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系.
2020年秋沪科版八年级数学上册第14章全等三角形单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列物品不是利用三角形稳定性的是
A.自行车的三角形车架
B.三角形房架
C.照相机的三脚架
D.放缩尺
2.如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠3=∠4
3.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是
A.76°
B.62°
C.42°
D.76°,62°或42°都可以
4.如图,AC⊥BD于点P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP的条件有
A.0个
B.1个
C.2个
D.3个
5.下列选项中,能使两个直角三角形全等的是
A.一组锐角对应相等
B.两组锐角对应相等
C.一组对边对应相等
D.两组对边对应相等
6.下列说法正确的是
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
7.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于
A.∠EDB
B.∠AFB
C.∠BED
D.∠ABF
8.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一直线上,∠BCE=120°,则∠ADC的度数是
A.55°
B.60°
C.75°
D.70°
9.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5
cm,DE=1.7
cm,则BE的长为
A.0.8
cm
B.0.7
cm
C.0.6
cm
D.1
cm
10.如图,在四边形ABCD中,AC平分∠BAD,AD=AC,在AC上截取AE=AB,连接DE,BE,并延长BE交CD于点F,以下结论:①△BAC≌△EAD;②∠ABE+∠ADE=∠BCD;③BC+CF=DE+EF.其中正确的有
A.
0个
B.
1个
C.
2个
D.
3个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,△ABC≌△EDF,AE=20
cm,FC=10
cm,则AC的长为 15 cm.?
12.如图,点F,C在线段BE上,且∠1=∠2,AC=DF,若要使△ABC≌△DEF,则还要补充一个条件 ∠A=∠D(答案不唯一,合理即可) .?
13.如图,AD是△ABC中BC边上的中线.若AB=5,AC=8,则AD的取值范围是 1.5
三、解答题(本大题共6小题,满分60分)
15.(8分)如图,在△ADF和△CBE中,点A,E,F,C在同一直线上,已知AD∥BC,AD=CB,∠B=∠D.求证:AE=CF.
证明:∵AD∥BC,∴∠A=∠C,在△ADF和△CBE中,
∴△ADF≌△CBE,∴AF=CE,∴AE=CF.
16.(8分)在Rt△ABC中,∠ACB=90°,BC=2
cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5
cm,求AE的长.
解:∵EF⊥AC,∴∠FEC=90°.∵∠ACB=90°,∴∠ACB=∠FEC,∠ECF+∠BCD=90°,∵CD⊥AB,∴∠BCD+∠B=90°,∴∠ECF=∠B.
在△ABC和△FCE中,∴△FCE≌△ABC(ASA),∴EF=AC.
∵BC=2
cm,EF=5
cm,∴AE=AC-CE=5-2=3
cm.
17.(10分)小明家所在的小区有一个池塘,如图,A,B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在BD的中点C处有一个雕塑,小明从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A,B两点之间的距离.
(1)你能说明小明这样做的根据吗?
(2)如果小明未带测量工具,但是知道A和假山、雕塑分别相距200米、120米,你能帮助他确定AB的长度范围吗?
解:(1)在△ACB和△ECD中,∴△ACB≌△ECD(SAS),∴DE=AB.
(2)连接AD.
∵AD=200米,AC=120米,∴AE=240米,∴40米
(1)求证:△AEC≌△BED;
(2)若∠1=48°,求∠BDE的度数.
解:(1)∵∠A=∠B,∠BOE=∠AOD,∴∠2=∠BEA,∵∠1=∠2,∴∠BEA=∠1.
∴∠BEA+∠AED=∠1+∠AED,即∠BED=∠AEC,
在△AEC和△BED中,∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,∴EC=ED,∠C=∠BDE,∴∠C=∠EDC,
∵∠1=48°,∴∠C=∠EDC=66°,∴∠BDE=66°.
19.(12分)如图,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,CE与BF相交于点M.
求证:(1)EC=BF;
(2)EC⊥BF.
证明:(1)∵AE⊥AB,AF⊥AC,∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF.
在△EAC和△BAF中,∴△EAC≌△BAF(SAS),∴EC=BF.
(2)∵△EAC≌△BAF,∴∠AEC=∠ABF,又∵∠AEB+∠ABE=90°,
∴∠CEB+∠ABF+∠EBA=90°,∴∠MEB+∠EBM=90°,即∠EMB=90°,∴EC⊥BF.
20.(12分)已知∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1,①线段CD和BE的数量关系是 CD=BE ;?
②请写出线段AD,BE,DE之间的数量关系并证明.
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系.
解:(1)②AD=BE+DE.
理由:∵∠ACB=90°,AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠B=90°,∴∠ACD=∠B.
在△ACD和△CBE中,∴△ACD≌△CBE,∴AD=CE,CD=BE,
∵CE=CD+DE=BE+DE,∴AD=BE+DE.
(2)②中的结论不成立,DE=AD+BE.
