2020年秋沪科版八年级数学上册第13章三角形中的边角关系命题与证明单元测试卷(word含答案)
文档属性
| 名称 | 2020年秋沪科版八年级数学上册第13章三角形中的边角关系命题与证明单元测试卷(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 276.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 07:17:57 | ||
图片预览




文档简介
2020年秋沪科版八年级数学上册第13章三角形中的边角关系命题与证明单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列语句不是命题的是
A.北京是中国的首都
B.绝对值大的数较大
C.垂线段最短
D.今天下雨了吗
2.已知三角形两边的长分别是1和5,则此三角形第三边的长可能是
A.4
B.5
C.6
D.7
3.已知a,b,c为三角形三边的长,则化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|的结果是
A.0
B.2a+2b+2c
C.4a
D.2b-2c
4.如图,四个图形中,线段BE是△ABC的高的图是
5.如图,BD⊥AC于点D,则图中以BD为高的三角形的个数是
A.3
B.4
C.5
D.6
6.下列命题的逆命题是真命题的是
A.同位角相等
B.对顶角相等
C.钝角三角形有两个锐角
D.两直线平行,内错角相等
7.如图,已知∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F=
A.180°
B.360°
C.240°
D.200°
8.如图,△ABC纸片中∠A=56°,∠C=88°.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则∠EDB的度数为
A.76°
B.74°
C.72°
D.70°
9.光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2等于
A.52°
B.61°
C.65°
D.70°
10.如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则S△ABC=
A.40
B.35
C.30
D.25
二、填空题(本大题共4小题,每小题5分,满分20分)
11.设三角形三边长分别为3,7,1+a,则a的取值范围为 .?
12.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为25°,那么这个“半角三角形”的最大内角的度数为 .?
13.已知一个等腰三角形的底边长为5
cm,一腰上的中线把其周长分成差为1
cm的两部分,则其腰长为 .?
14.已知点A(4,0),B(0,5),点C在x轴上,且△BOC的面积是△ABC的面积的3倍,那么点C的坐标为 .?
三、解答题(本大题共6小题,满分60分)
15.(8分)写出下列命题的逆命题,并指出其真假.
(1)如果a,b都是偶数,那么a+b是偶数;
(2)两个锐角的和是钝角;
(3)直角三角形的两个锐角互余.
16.(8分)已知a,b,c为△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,求△ABC的周长并判断△ABC的形状.
17.(10分)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
18.(10分)数学课上,张老师举了下面的例题:
例1:等腰△ABC中,∠A=110°,求∠B的度数.
例2:等腰△ABC中,∠A=40°,求∠B的度数.
爱思考的小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰△ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
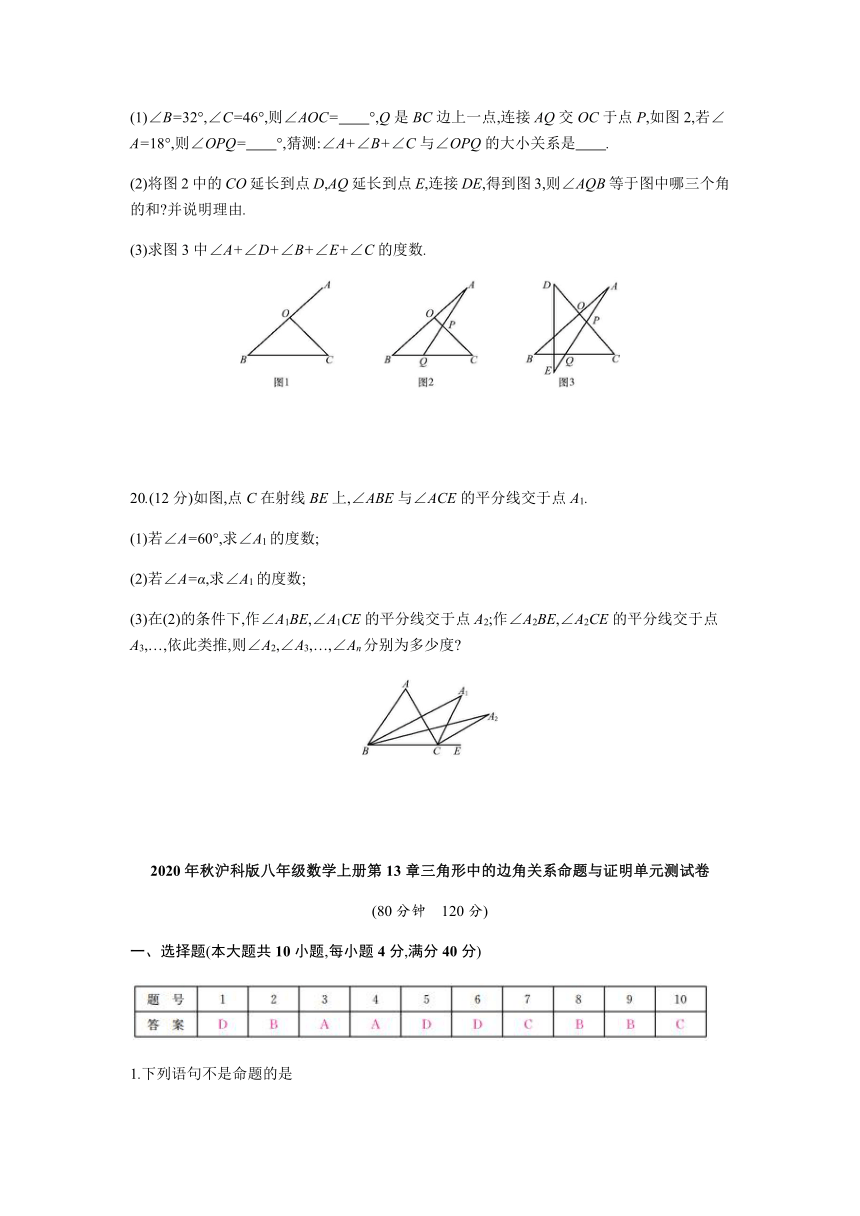
19.(12分)如图1,在△OBC中,A是BO延长线上的一点.
(1)∠B=32°,∠C=46°,则∠AOC= °,Q是BC边上一点,连接AQ交OC于点P,如图2,若∠A=18°,则∠OPQ= °,猜测:∠A+∠B+∠C与∠OPQ的大小关系是 .?
(2)将图2中的CO延长到点D,AQ延长到点E,连接DE,得到图3,则∠AQB等于图中哪三个角的和?并说明理由.
(3)求图3中∠A+∠D+∠B+∠E+∠C的度数.
20.(12分)如图,点C在射线BE上,∠ABE与∠ACE的平分线交于点A1.
(1)若∠A=60°,求∠A1的度数;
(2)若∠A=α,求∠A1的度数;
(3)在(2)的条件下,作∠A1BE,∠A1CE的平分线交于点A2;作∠A2BE,∠A2CE的平分线交于点A3,…,依此类推,则∠A2,∠A3,…,∠An分别为多少度?
2020年秋沪科版八年级数学上册第13章三角形中的边角关系命题与证明单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列语句不是命题的是
A.北京是中国的首都
B.绝对值大的数较大
C.垂线段最短
D.今天下雨了吗
2.已知三角形两边的长分别是1和5,则此三角形第三边的长可能是
A.4
B.5
C.6
D.7
3.已知a,b,c为三角形三边的长,则化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|的结果是
A.0
B.2a+2b+2c
C.4a
D.2b-2c
4.如图,四个图形中,线段BE是△ABC的高的图是
5.如图,BD⊥AC于点D,则图中以BD为高的三角形的个数是
A.3
B.4
C.5
D.6
6.下列命题的逆命题是真命题的是
A.同位角相等
B.对顶角相等
C.钝角三角形有两个锐角
D.两直线平行,内错角相等
7.如图,已知∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F=
A.180°
B.360°
C.240°
D.200°
8.如图,△ABC纸片中∠A=56°,∠C=88°.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则∠EDB的度数为
A.76°
B.74°
C.72°
D.70°
9.光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2等于
A.52°
B.61°
C.65°
D.70°
10.如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则S△ABC=
A.40
B.35
C.30
D.25
二、填空题(本大题共4小题,每小题5分,满分20分)
11.设三角形三边长分别为3,7,1+a,则a的取值范围为 312.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为25°,那么这个“半角三角形”的最大内角的度数为 105° .?
13.已知一个等腰三角形的底边长为5
cm,一腰上的中线把其周长分成差为1
cm的两部分,则其腰长为 6
cm或4
cm .?
14.已知点A(4,0),B(0,5),点C在x轴上,且△BOC的面积是△ABC的面积的3倍,那么点C的坐标为 (3,0)或(6,0) .?
三、解答题(本大题共6小题,满分60分)
15.(8分)写出下列命题的逆命题,并指出其真假.
(1)如果a,b都是偶数,那么a+b是偶数;
(2)两个锐角的和是钝角;
(3)直角三角形的两个锐角互余.
解:(1)逆命题是:如果a+b是偶数,那么a,b都是偶数.这是假命题.
(2)逆命题是:如果两个角的和是钝角,那么这两个角是锐角.这是假命题.
(3)逆命题是:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形.这是真命题.
16.(8分)已知a,b,c为△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,求△ABC的周长并判断△ABC的形状.
解:∵(b-2)2≥0,|c-3|≥0,且(b-2)2+|c-3|=0,
∴b-2=0,c-3=0,∴b=2,c=3.
∵a为方程|x-4|=2的解,∴a=2或6.
经检验,当a=6时,不满足三角形三边关系定理,舍去.
∴a=2,b=2,c=3.
∴△ABC为等腰三角形,周长为7.
17.(10分)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,∴∠CBE=∠CBD=65°.
(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.
∵DF∥BE,∴∠F=∠CEB=25°.
18.(10分)数学课上,张老师举了下面的例题:
例1:等腰△ABC中,∠A=110°,求∠B的度数.
例2:等腰△ABC中,∠A=40°,求∠B的度数.
爱思考的小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰△ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
解:分两种情况:
当90≤x<180时,∠A只能为顶角,∴∠B的度数只有一个;
当0若∠A为底角,则∠B=x°或∠B=(180-2x)°.
当≠180-2x且≠x且180-2x≠x,即x≠60时,∠B有三个不同的度数.
综上,当019.(12分)如图1,在△OBC中,A是BO延长线上的一点.
(1)∠B=32°,∠C=46°,则∠AOC= 78 °,Q是BC边上一点,连接AQ交OC于点P,如图2,若∠A=18°,则∠OPQ= 96 °,猜测:∠A+∠B+∠C与∠OPQ的大小关系是 ∠A+∠B+∠C=∠OPQ .?
(2)将图2中的CO延长到点D,AQ延长到点E,连接DE,得到图3,则∠AQB等于图中哪三个角的和?并说明理由.
(3)求图3中∠A+∠D+∠B+∠E+∠C的度数.
解:(2)∠AQB=∠C+∠D+∠E.
理由:∵∠EPC=∠D+∠E,∠AQB=∠C+∠EPC,
∴∠AQB=∠C+∠D+∠E.
(3)由(2)知∠AQB=∠C+∠D+∠E,又∵∠AQB+∠A+∠B=180°,∴∠A+∠D+∠B+∠E+∠C=180°.
20.(12分)如图,点C在射线BE上,∠ABE与∠ACE的平分线交于点A1.
(1)若∠A=60°,求∠A1的度数;
(2)若∠A=α,求∠A1的度数;
(3)在(2)的条件下,作∠A1BE,∠A1CE的平分线交于点A2;作∠A2BE,∠A2CE的平分线交于点A3,…,依此类推,则∠A2,∠A3,…,∠An分别为多少度?
解:(1)∵∠ACE=∠A+∠ABC,∠ABE和∠ACE的平分线交于点A1,
∴∠A1BC=∠ABC,∠A1CE=∠ACE,
∴∠A1CE=∠ACE=(∠A+∠ABC)=∠ABC+∠A,
又∵∠A1CE=∠A1+∠A1BC=∠A1+∠ABC,
∴∠A1=∠A=30°.
(2)∠A1=α.
(3)∠A2=α,∠A3=α,∠An=α.
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列语句不是命题的是
A.北京是中国的首都
B.绝对值大的数较大
C.垂线段最短
D.今天下雨了吗
2.已知三角形两边的长分别是1和5,则此三角形第三边的长可能是
A.4
B.5
C.6
D.7
3.已知a,b,c为三角形三边的长,则化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|的结果是
A.0
B.2a+2b+2c
C.4a
D.2b-2c
4.如图,四个图形中,线段BE是△ABC的高的图是
5.如图,BD⊥AC于点D,则图中以BD为高的三角形的个数是
A.3
B.4
C.5
D.6
6.下列命题的逆命题是真命题的是
A.同位角相等
B.对顶角相等
C.钝角三角形有两个锐角
D.两直线平行,内错角相等
7.如图,已知∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F=
A.180°
B.360°
C.240°
D.200°
8.如图,△ABC纸片中∠A=56°,∠C=88°.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则∠EDB的度数为
A.76°
B.74°
C.72°
D.70°
9.光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2等于
A.52°
B.61°
C.65°
D.70°
10.如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则S△ABC=
A.40
B.35
C.30
D.25
二、填空题(本大题共4小题,每小题5分,满分20分)
11.设三角形三边长分别为3,7,1+a,则a的取值范围为 .?
12.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为25°,那么这个“半角三角形”的最大内角的度数为 .?
13.已知一个等腰三角形的底边长为5
cm,一腰上的中线把其周长分成差为1
cm的两部分,则其腰长为 .?
14.已知点A(4,0),B(0,5),点C在x轴上,且△BOC的面积是△ABC的面积的3倍,那么点C的坐标为 .?
三、解答题(本大题共6小题,满分60分)
15.(8分)写出下列命题的逆命题,并指出其真假.
(1)如果a,b都是偶数,那么a+b是偶数;
(2)两个锐角的和是钝角;
(3)直角三角形的两个锐角互余.
16.(8分)已知a,b,c为△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,求△ABC的周长并判断△ABC的形状.
17.(10分)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
18.(10分)数学课上,张老师举了下面的例题:
例1:等腰△ABC中,∠A=110°,求∠B的度数.
例2:等腰△ABC中,∠A=40°,求∠B的度数.
爱思考的小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰△ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
19.(12分)如图1,在△OBC中,A是BO延长线上的一点.
(1)∠B=32°,∠C=46°,则∠AOC= °,Q是BC边上一点,连接AQ交OC于点P,如图2,若∠A=18°,则∠OPQ= °,猜测:∠A+∠B+∠C与∠OPQ的大小关系是 .?
(2)将图2中的CO延长到点D,AQ延长到点E,连接DE,得到图3,则∠AQB等于图中哪三个角的和?并说明理由.
(3)求图3中∠A+∠D+∠B+∠E+∠C的度数.
20.(12分)如图,点C在射线BE上,∠ABE与∠ACE的平分线交于点A1.
(1)若∠A=60°,求∠A1的度数;
(2)若∠A=α,求∠A1的度数;
(3)在(2)的条件下,作∠A1BE,∠A1CE的平分线交于点A2;作∠A2BE,∠A2CE的平分线交于点A3,…,依此类推,则∠A2,∠A3,…,∠An分别为多少度?
2020年秋沪科版八年级数学上册第13章三角形中的边角关系命题与证明单元测试卷
(80分钟 120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列语句不是命题的是
A.北京是中国的首都
B.绝对值大的数较大
C.垂线段最短
D.今天下雨了吗
2.已知三角形两边的长分别是1和5,则此三角形第三边的长可能是
A.4
B.5
C.6
D.7
3.已知a,b,c为三角形三边的长,则化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|的结果是
A.0
B.2a+2b+2c
C.4a
D.2b-2c
4.如图,四个图形中,线段BE是△ABC的高的图是
5.如图,BD⊥AC于点D,则图中以BD为高的三角形的个数是
A.3
B.4
C.5
D.6
6.下列命题的逆命题是真命题的是
A.同位角相等
B.对顶角相等
C.钝角三角形有两个锐角
D.两直线平行,内错角相等
7.如图,已知∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F=
A.180°
B.360°
C.240°
D.200°
8.如图,△ABC纸片中∠A=56°,∠C=88°.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则∠EDB的度数为
A.76°
B.74°
C.72°
D.70°
9.光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2等于
A.52°
B.61°
C.65°
D.70°
10.如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则S△ABC=
A.40
B.35
C.30
D.25
二、填空题(本大题共4小题,每小题5分,满分20分)
11.设三角形三边长分别为3,7,1+a,则a的取值范围为 3
13.已知一个等腰三角形的底边长为5
cm,一腰上的中线把其周长分成差为1
cm的两部分,则其腰长为 6
cm或4
cm .?
14.已知点A(4,0),B(0,5),点C在x轴上,且△BOC的面积是△ABC的面积的3倍,那么点C的坐标为 (3,0)或(6,0) .?
三、解答题(本大题共6小题,满分60分)
15.(8分)写出下列命题的逆命题,并指出其真假.
(1)如果a,b都是偶数,那么a+b是偶数;
(2)两个锐角的和是钝角;
(3)直角三角形的两个锐角互余.
解:(1)逆命题是:如果a+b是偶数,那么a,b都是偶数.这是假命题.
(2)逆命题是:如果两个角的和是钝角,那么这两个角是锐角.这是假命题.
(3)逆命题是:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形.这是真命题.
16.(8分)已知a,b,c为△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|x-4|=2的解,求△ABC的周长并判断△ABC的形状.
解:∵(b-2)2≥0,|c-3|≥0,且(b-2)2+|c-3|=0,
∴b-2=0,c-3=0,∴b=2,c=3.
∵a为方程|x-4|=2的解,∴a=2或6.
经检验,当a=6时,不满足三角形三边关系定理,舍去.
∴a=2,b=2,c=3.
∴△ABC为等腰三角形,周长为7.
17.(10分)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,∴∠CBE=∠CBD=65°.
(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.
∵DF∥BE,∴∠F=∠CEB=25°.
18.(10分)数学课上,张老师举了下面的例题:
例1:等腰△ABC中,∠A=110°,求∠B的度数.
例2:等腰△ABC中,∠A=40°,求∠B的度数.
爱思考的小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰△ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
解:分两种情况:
当90≤x<180时,∠A只能为顶角,∴∠B的度数只有一个;
当0
当≠180-2x且≠x且180-2x≠x,即x≠60时,∠B有三个不同的度数.
综上,当0
(1)∠B=32°,∠C=46°,则∠AOC= 78 °,Q是BC边上一点,连接AQ交OC于点P,如图2,若∠A=18°,则∠OPQ= 96 °,猜测:∠A+∠B+∠C与∠OPQ的大小关系是 ∠A+∠B+∠C=∠OPQ .?
(2)将图2中的CO延长到点D,AQ延长到点E,连接DE,得到图3,则∠AQB等于图中哪三个角的和?并说明理由.
(3)求图3中∠A+∠D+∠B+∠E+∠C的度数.
解:(2)∠AQB=∠C+∠D+∠E.
理由:∵∠EPC=∠D+∠E,∠AQB=∠C+∠EPC,
∴∠AQB=∠C+∠D+∠E.
(3)由(2)知∠AQB=∠C+∠D+∠E,又∵∠AQB+∠A+∠B=180°,∴∠A+∠D+∠B+∠E+∠C=180°.
20.(12分)如图,点C在射线BE上,∠ABE与∠ACE的平分线交于点A1.
(1)若∠A=60°,求∠A1的度数;
(2)若∠A=α,求∠A1的度数;
(3)在(2)的条件下,作∠A1BE,∠A1CE的平分线交于点A2;作∠A2BE,∠A2CE的平分线交于点A3,…,依此类推,则∠A2,∠A3,…,∠An分别为多少度?
解:(1)∵∠ACE=∠A+∠ABC,∠ABE和∠ACE的平分线交于点A1,
∴∠A1BC=∠ABC,∠A1CE=∠ACE,
∴∠A1CE=∠ACE=(∠A+∠ABC)=∠ABC+∠A,
又∵∠A1CE=∠A1+∠A1BC=∠A1+∠ABC,
∴∠A1=∠A=30°.
(2)∠A1=α.
(3)∠A2=α,∠A3=α,∠An=α.
