人教版数学八年级上册13.1.2 线段的垂直平分线的性质同步练习(共2课时 word 版 含答案)
文档属性
| 名称 | 人教版数学八年级上册13.1.2 线段的垂直平分线的性质同步练习(共2课时 word 版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 00:00:00 | ||
图片预览



文档简介
13.1.2 线段的垂直平分线的性质
第1课时 线段的垂直平分线的性质和判定
1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为(
)
A.6
B.5
C.4
D.3
2.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为点E,请任意写出一组相等的线段
.
第2题图
第3题图
3.如图,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是
.
4.如图,点D在BC上,DE垂直平分AC,垂足为E,DF垂直平分BA,垂足为F.求证:DB=DC.
5.如图,点P是△ABC内的一点,若PB=PC,则(
)
A.点P在∠ABC的平分线上
B.点P在∠ACB的平分线上
C.点P在边AB的垂直平分线上
D.点P在边BC的垂直平分线上
6.如图,AB=AC,DB=DC,E是AD延长线上的一点,BE是否与CE相等?试说明理由.
7.如图,已知钝角△ABC,其中∠A是钝角,求作AC边上的高BH.
8.到三角形三个顶点的距离都相等的点是这个三角形的(
)
A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点
9.如图,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,用直线MN交BC于点D,连接AD,则∠BAD的度数为(
)
A.50°
B.60°
C.70°
D.80°
10.如图,AC是线段BD的垂直平分线,E是AC上的一点,则图中全等的三角形共有(
)
A.3对
B.4对
C.5对
D.6对
第10题图
第11题图
11.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为
cm.
12.如图,已知AB比AC长2
cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14
cm,求AB和AC的长.
13.如图,AD是△ABC的高,E为AD上的一点,且BE=CE,求证:直线AE是BC的垂直平分线.
14.如图,在△ABC中,BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交AC于点G.求证:
(1)BF=CG;
(2)AF=(AB+AC).
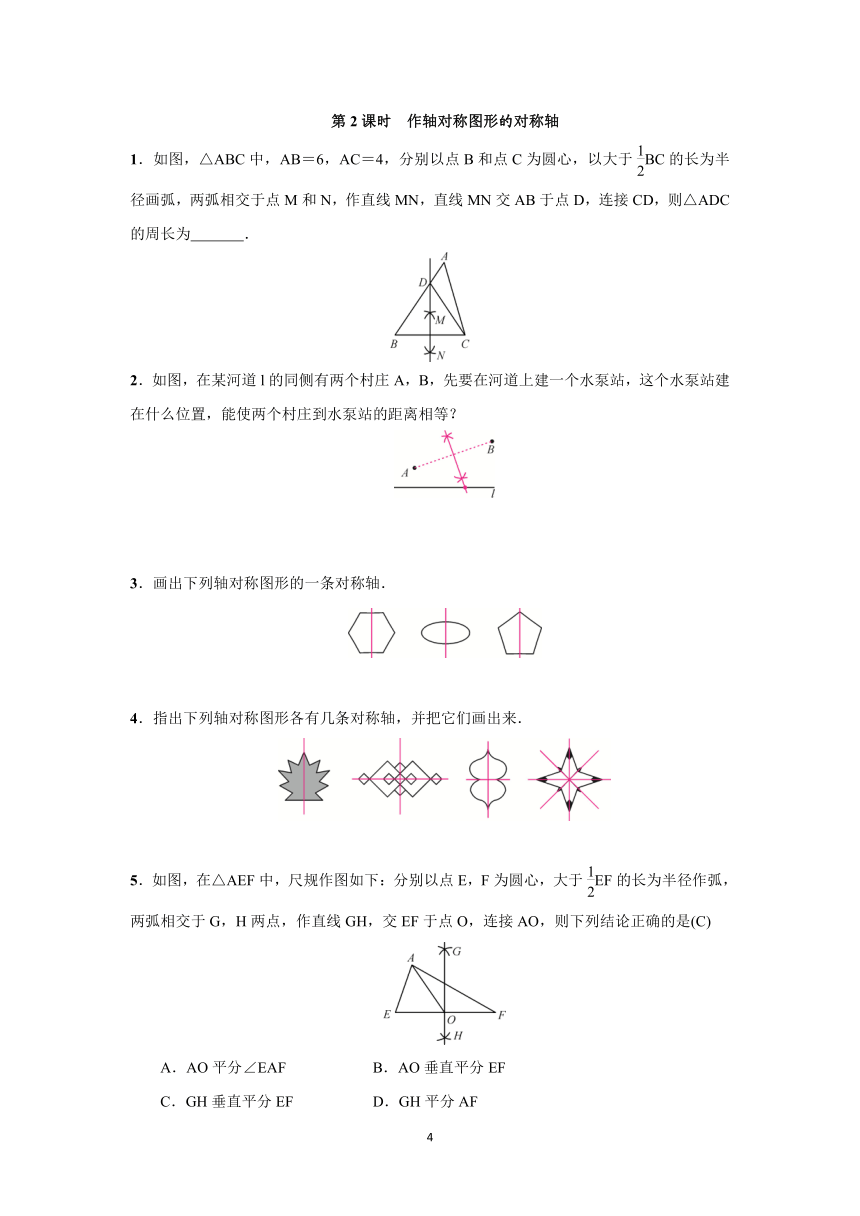
第2课时 作轴对称图形的对称轴
1.如图,△ABC中,AB=6,AC=4,分别以点B和点C为圆心,以大于BC的长为半径画弧,两弧相交于点M和N,作直线MN,直线MN交AB于点D,连接CD,则△ADC的周长为
.
2.如图,在某河道l的同侧有两个村庄A,B,先要在河道上建一个水泵站,这个水泵站建在什么位置,能使两个村庄到水泵站的距离相等?
3.画出下列轴对称图形的一条对称轴.
4.指出下列轴对称图形各有几条对称轴,并把它们画出来.
5.如图,在△AEF中,尺规作图如下:分别以点E,F为圆心,大于EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是(C)
AO平分∠EAF
B.AO垂直平分EF
C.GH垂直平分EF
D.GH平分AF
6.如图,AO,BO是两条笔直的交叉公路,M,N是两个村庄,现准备建一个联通信号塔,要求信号塔到两个村庄的距离相等,并且到两条公路的距离也相等,同时在∠AOB所在区域内.信号塔应修在什么位置?在图中标出塔的位置.
7.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角α的数量关系.
参考答案:
13.1.2 线段的垂直平分线的性质
第1课时 线段的垂直平分线的性质和判定
1.B
2.
BD=DA(或BE=EA或CD=ED).
3.
16.
4.
证明:连接AD,∵DE垂直平分AC,DF垂直平分BA,
∴DB=DA,DC=DA.
∴DB=DC.
5.D
6.
解:相等.
理由:连接BC.∵AB=AC,
∴点A在线段BC的垂直平分线上.
同理:点D也在线段BC的垂直平分线上.
∵两点确定一条直线,
∴AD是线段BC的垂直平分线.
∵E是AD延长线上的一点,
∴BE=CE.
7.
解:作法:①延长线段CA至点E,任意取一点K,使点K和点B在CE的两侧;
②以点B为圆心,BK长为半径画弧,交CE于点F和G;
③分别以点F和G为圆心,大于FG的长为半径画弧,两弧相交于点M;
④作直线BM,交CE于点H.则线段BH就是所求作的高.如图所示.
8.D
9.C
10.D
11.
3
.
12.解:∵DE垂直平分BC,
∴DB=DC.
∵△ACD的周长是14
cm,
即AC+AD+DC=14
cm,
∴AC+AD+BD=14
cm,
即AC+AB=14
cm.
又∵AB-AC=2
cm,
∴AB=8
cm,AC=6
cm.
13.证明:在Rt△BDE和Rt△CDE中,
∴Rt△BDE≌Rt△CDE(HL).
∴∠BED=∠CED.
∴∠AEB=∠AEC.
在△ABE和△ACE中,
∴△ABE≌△ACE(SAS).
∴AB=AC.
∴点A在BC的垂直平分线上.
又∵BE=CE,
∴点E在BC的垂直平分线上.
∴直线AE是BC的垂直平分线.
14.
证明:(1)连接BE,CE.
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴EF=EG.
∵DE垂直平分BC,
∴EB=EC.
在Rt△EFB和Rt△EGC中,
∴Rt△EFB≌Rt△EGC(HL).
∴BF=CG.
(2)∵BF=CG,
∴AB+AC=AB+BF+AG=AF+AG.
在Rt△AEF和Rt△AEG中,
∴Rt△AEF≌Rt△AEG(HL).
∴AF=AG.
∴AF=(AB+AC).
第2课时 作轴对称图形的对称轴
1.
10.
2.
解:连接AB,作线段AB的垂直平分线,与直线l的交点P即为所求作的点.如图.
3.
解:如图.
4.
解:4个图形对称轴的条数分别为1条、2条、2条、4条.如图.
5.C
6.
解:∠AOB的平分线与线段MN的垂直平分线的交点即为塔的位置,图略.
7.
解:(1)如图所示.
(2)连接BO,B′O,B″O.∵△ABC和△A′B′C′关于直线MN对称,
∴∠BOM=∠B′OM.
又∵△A′B′C′和△A″B″C″关于直线EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α,
即∠BOB″=2α.
第1课时 线段的垂直平分线的性质和判定
1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为(
)
A.6
B.5
C.4
D.3
2.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为点E,请任意写出一组相等的线段
.
第2题图
第3题图
3.如图,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是
.
4.如图,点D在BC上,DE垂直平分AC,垂足为E,DF垂直平分BA,垂足为F.求证:DB=DC.
5.如图,点P是△ABC内的一点,若PB=PC,则(
)
A.点P在∠ABC的平分线上
B.点P在∠ACB的平分线上
C.点P在边AB的垂直平分线上
D.点P在边BC的垂直平分线上
6.如图,AB=AC,DB=DC,E是AD延长线上的一点,BE是否与CE相等?试说明理由.
7.如图,已知钝角△ABC,其中∠A是钝角,求作AC边上的高BH.
8.到三角形三个顶点的距离都相等的点是这个三角形的(
)
A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点
9.如图,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,用直线MN交BC于点D,连接AD,则∠BAD的度数为(
)
A.50°
B.60°
C.70°
D.80°
10.如图,AC是线段BD的垂直平分线,E是AC上的一点,则图中全等的三角形共有(
)
A.3对
B.4对
C.5对
D.6对
第10题图
第11题图
11.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为
cm.
12.如图,已知AB比AC长2
cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14
cm,求AB和AC的长.
13.如图,AD是△ABC的高,E为AD上的一点,且BE=CE,求证:直线AE是BC的垂直平分线.
14.如图,在△ABC中,BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交AC于点G.求证:
(1)BF=CG;
(2)AF=(AB+AC).
第2课时 作轴对称图形的对称轴
1.如图,△ABC中,AB=6,AC=4,分别以点B和点C为圆心,以大于BC的长为半径画弧,两弧相交于点M和N,作直线MN,直线MN交AB于点D,连接CD,则△ADC的周长为
.
2.如图,在某河道l的同侧有两个村庄A,B,先要在河道上建一个水泵站,这个水泵站建在什么位置,能使两个村庄到水泵站的距离相等?
3.画出下列轴对称图形的一条对称轴.
4.指出下列轴对称图形各有几条对称轴,并把它们画出来.
5.如图,在△AEF中,尺规作图如下:分别以点E,F为圆心,大于EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是(C)
AO平分∠EAF
B.AO垂直平分EF
C.GH垂直平分EF
D.GH平分AF
6.如图,AO,BO是两条笔直的交叉公路,M,N是两个村庄,现准备建一个联通信号塔,要求信号塔到两个村庄的距离相等,并且到两条公路的距离也相等,同时在∠AOB所在区域内.信号塔应修在什么位置?在图中标出塔的位置.
7.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角α的数量关系.
参考答案:
13.1.2 线段的垂直平分线的性质
第1课时 线段的垂直平分线的性质和判定
1.B
2.
BD=DA(或BE=EA或CD=ED).
3.
16.
4.
证明:连接AD,∵DE垂直平分AC,DF垂直平分BA,
∴DB=DA,DC=DA.
∴DB=DC.
5.D
6.
解:相等.
理由:连接BC.∵AB=AC,
∴点A在线段BC的垂直平分线上.
同理:点D也在线段BC的垂直平分线上.
∵两点确定一条直线,
∴AD是线段BC的垂直平分线.
∵E是AD延长线上的一点,
∴BE=CE.
7.
解:作法:①延长线段CA至点E,任意取一点K,使点K和点B在CE的两侧;
②以点B为圆心,BK长为半径画弧,交CE于点F和G;
③分别以点F和G为圆心,大于FG的长为半径画弧,两弧相交于点M;
④作直线BM,交CE于点H.则线段BH就是所求作的高.如图所示.
8.D
9.C
10.D
11.
3
.
12.解:∵DE垂直平分BC,
∴DB=DC.
∵△ACD的周长是14
cm,
即AC+AD+DC=14
cm,
∴AC+AD+BD=14
cm,
即AC+AB=14
cm.
又∵AB-AC=2
cm,
∴AB=8
cm,AC=6
cm.
13.证明:在Rt△BDE和Rt△CDE中,
∴Rt△BDE≌Rt△CDE(HL).
∴∠BED=∠CED.
∴∠AEB=∠AEC.
在△ABE和△ACE中,
∴△ABE≌△ACE(SAS).
∴AB=AC.
∴点A在BC的垂直平分线上.
又∵BE=CE,
∴点E在BC的垂直平分线上.
∴直线AE是BC的垂直平分线.
14.
证明:(1)连接BE,CE.
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴EF=EG.
∵DE垂直平分BC,
∴EB=EC.
在Rt△EFB和Rt△EGC中,
∴Rt△EFB≌Rt△EGC(HL).
∴BF=CG.
(2)∵BF=CG,
∴AB+AC=AB+BF+AG=AF+AG.
在Rt△AEF和Rt△AEG中,
∴Rt△AEF≌Rt△AEG(HL).
∴AF=AG.
∴AF=(AB+AC).
第2课时 作轴对称图形的对称轴
1.
10.
2.
解:连接AB,作线段AB的垂直平分线,与直线l的交点P即为所求作的点.如图.
3.
解:如图.
4.
解:4个图形对称轴的条数分别为1条、2条、2条、4条.如图.
5.C
6.
解:∠AOB的平分线与线段MN的垂直平分线的交点即为塔的位置,图略.
7.
解:(1)如图所示.
(2)连接BO,B′O,B″O.∵△ABC和△A′B′C′关于直线MN对称,
∴∠BOM=∠B′OM.
又∵△A′B′C′和△A″B″C″关于直线EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α,
即∠BOB″=2α.
