等腰三角形的判定
图片预览







文档简介
(共31张PPT)
等腰三角形的判定
我们在上一节学习了等腰三角形的性质。现在能回答一些问题吗?
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
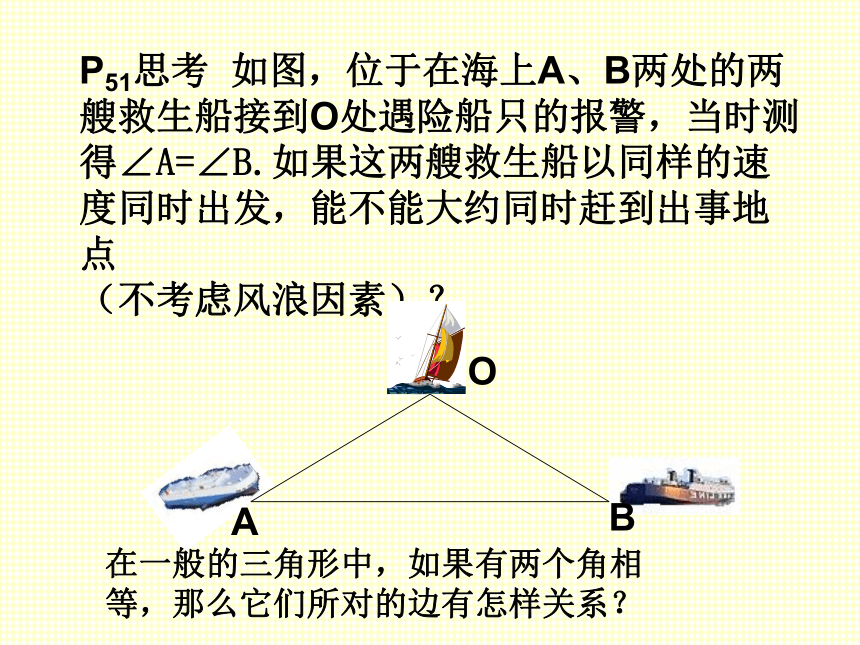
P51思考 如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点
(不考虑风浪因素)?
O
B
A
在一般的三角形中,如果有两个角相等,那么它们所对的边有怎样关系?
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边
用符号语言表示
∵
AB=AC (等边对等角)
∴
在⊿ABC中,∠B=∠C
等腰三角形的判定定理 与性质定理有何不同?
探究:
等腰三角形的性质定理和判定定理 互为逆命题
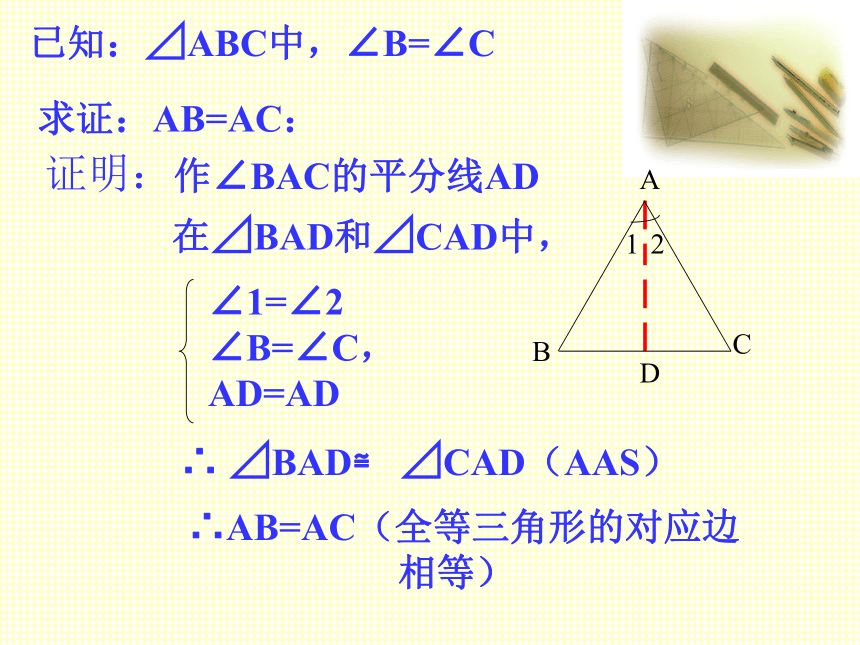
已知:⊿ABC中,∠B=∠C
求证:AB=AC:
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
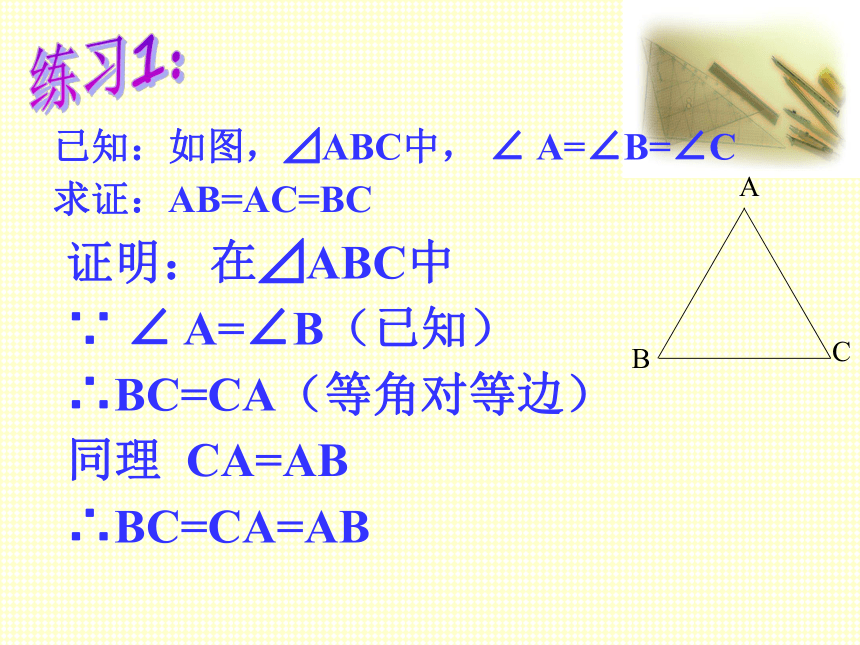
已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理 CA=AB
∴BC=CA=AB
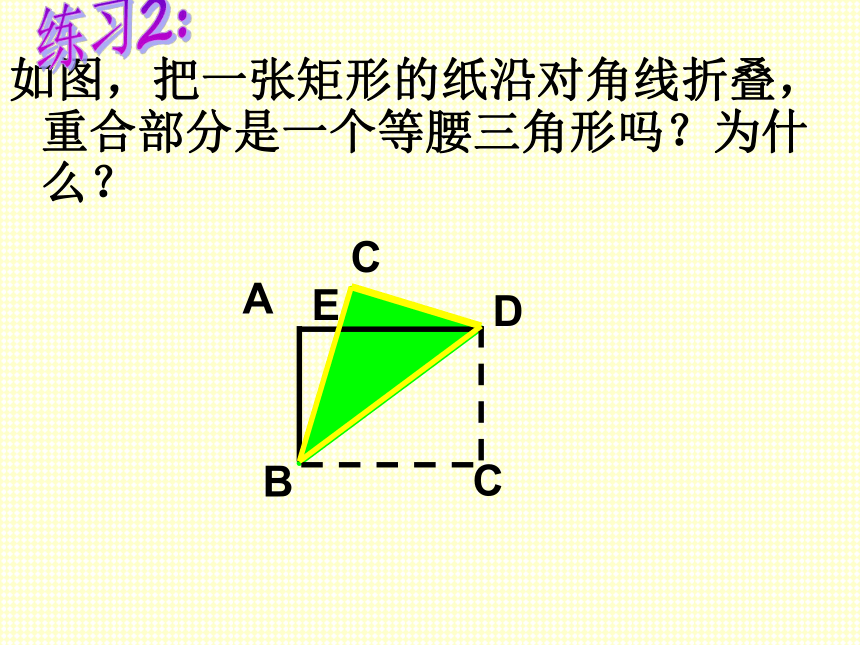
如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?
A
B
C
E
D
C
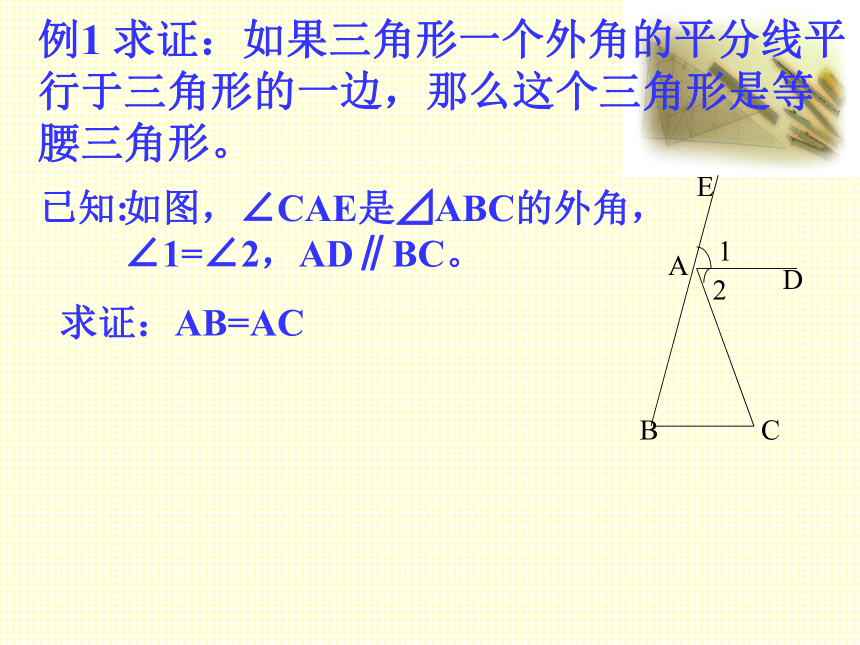
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
如图,∠CAE是⊿ABC的外角,
∠1=∠2,AD∥BC。
已知:
求证:AB=AC
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等)
∠2=∠C(两直线平行,
内错角相等)
∵∠1=∠2
∴∠B=∠C
∴AB=AC(等边对等角)
A
B
C
D
E
1
2
4、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。
O
C
D
B
A
练习4
C
B
A
D
1
2
解答
已知:如图, ∠A= ∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
解:
∠1=720 ∠2=360
等腰三角形有: ⊿ABC
⊿ABD
⊿BCD
C
B
A
D
1
2
练习5
已知:如图,CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形。
解答
A
C
D
B
A
C
D
B
解答
等腰直角三角形有: ⊿ABC ⊿ACD ⊿BCD
练习6
B
A
D
C
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
解答
B
A
D
C
证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD(等角对等边)
研究性学习
如果过等腰三角形的一个顶点的直线把原三角形分成两个等腰三角形,那么原等腰三角形的顶角可能是多少度?请你画出图形,并结合图形说明理由。
1、等腰三角形的判定定理及其推论的内容是什么?
判定定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。 。
2、等腰三角形的判定方法有下列几种:
①定义
②判定定理
3、等腰三角形的判定定理与性质定理的区别是:
条件和结论刚好相反。
4、运用等腰三角形的判定定理时,应注意
在同一个三角形中。
A
C
B
D
E
如图,标杆AB高5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D,E两点拉两条绳子,使得点D,B,E在一条直线上。量得DE=4m,绳子CD和CE要多长?
用尺规画一个等腰三角形ABC,使得底边BC为3cm,底边上的高AD为5cm。
课堂作业:
课本P56:
第2,3,4题
思考题1
A
B
如图,线段AB的端点B在直线 上(AB与直线 不垂直),请在直线 上另找一点C,使ΔABC为等腰三角形,这样的点能找几个?你能说出它们的画法吗?
C1
C2
C3
C4
思考题2
如图,∠B=∠E, ∠C=∠D,BC=DE,
F为CD的中点,求证:AF⊥CD.
A
B
C
D
E
F
M
N
思考题3
如图,在ΔABC中,O是∠ABC和∠ACB角
平分线的交点,过O点作BC的平行线分别与AB和
AC交于M和N.
O
A
B
C
M
N
(1)图中有没有等腰三
角形?有几个?
(2)线段BM、CN与MN
的长度有什么关系?
角平分线+平行
等腰三角形
1
2
3
等腰三角形的判定
我们在上一节学习了等腰三角形的性质。现在能回答一些问题吗?
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
P51思考 如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点
(不考虑风浪因素)?
O
B
A
在一般的三角形中,如果有两个角相等,那么它们所对的边有怎样关系?
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边
用符号语言表示
∵
AB=AC (等边对等角)
∴
在⊿ABC中,∠B=∠C
等腰三角形的判定定理 与性质定理有何不同?
探究:
等腰三角形的性质定理和判定定理 互为逆命题
已知:⊿ABC中,∠B=∠C
求证:AB=AC:
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理 CA=AB
∴BC=CA=AB
如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?
A
B
C
E
D
C
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
如图,∠CAE是⊿ABC的外角,
∠1=∠2,AD∥BC。
已知:
求证:AB=AC
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等)
∠2=∠C(两直线平行,
内错角相等)
∵∠1=∠2
∴∠B=∠C
∴AB=AC(等边对等角)
A
B
C
D
E
1
2
4、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。
O
C
D
B
A
练习4
C
B
A
D
1
2
解答
已知:如图, ∠A= ∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
解:
∠1=720 ∠2=360
等腰三角形有: ⊿ABC
⊿ABD
⊿BCD
C
B
A
D
1
2
练习5
已知:如图,CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形。
解答
A
C
D
B
A
C
D
B
解答
等腰直角三角形有: ⊿ABC ⊿ACD ⊿BCD
练习6
B
A
D
C
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
解答
B
A
D
C
证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD(等角对等边)
研究性学习
如果过等腰三角形的一个顶点的直线把原三角形分成两个等腰三角形,那么原等腰三角形的顶角可能是多少度?请你画出图形,并结合图形说明理由。
1、等腰三角形的判定定理及其推论的内容是什么?
判定定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。 。
2、等腰三角形的判定方法有下列几种:
①定义
②判定定理
3、等腰三角形的判定定理与性质定理的区别是:
条件和结论刚好相反。
4、运用等腰三角形的判定定理时,应注意
在同一个三角形中。
A
C
B
D
E
如图,标杆AB高5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D,E两点拉两条绳子,使得点D,B,E在一条直线上。量得DE=4m,绳子CD和CE要多长?
用尺规画一个等腰三角形ABC,使得底边BC为3cm,底边上的高AD为5cm。
课堂作业:
课本P56:
第2,3,4题
思考题1
A
B
如图,线段AB的端点B在直线 上(AB与直线 不垂直),请在直线 上另找一点C,使ΔABC为等腰三角形,这样的点能找几个?你能说出它们的画法吗?
C1
C2
C3
C4
思考题2
如图,∠B=∠E, ∠C=∠D,BC=DE,
F为CD的中点,求证:AF⊥CD.
A
B
C
D
E
F
M
N
思考题3
如图,在ΔABC中,O是∠ABC和∠ACB角
平分线的交点,过O点作BC的平行线分别与AB和
AC交于M和N.
O
A
B
C
M
N
(1)图中有没有等腰三
角形?有几个?
(2)线段BM、CN与MN
的长度有什么关系?
角平分线+平行
等腰三角形
1
2
3
