六年级上册数学一课一练-5.3身高的情况 北师大版(含答案)
文档属性
| 名称 | 六年级上册数学一课一练-5.3身高的情况 北师大版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 221.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 16:07:48 | ||
图片预览

文档简介
六年级上册数学一课一练-5.3身高的情况
一、单选题
1.观察下边的折线统计图,哪一年实际产量超出计划产量最多( )。
A.?1999年????????????????????????????????????B.?2001年????????????????????????????????????C.?2002年
2.下面是阳光小学和实验小学学生四到六年级近视人数统计图。根据统计情况估计一下,哪个小学的近视人数更多?
A.?阳光小学??????????????????????????????????B.?实验小学??????????????????????????????????C.?不能确定
3.甲、乙两修路队修路情况如图所示,正确的说法是(??? )
A.?甲队一共比乙队多修3米??????????B.?两队的修路速度都在加快??????????C.?甲队每天修的都比乙队多
4.要表示六年一班男女同学的身高情况,需要选用( )。
A.?条形统计图??????????????????????????B.?复式折线统计图??????????????????????????C.?复式条形统计图
二、判断题
5.纵向复式条形统计图比横向复式条形统计图表示的更明白。
6.任意两个条形统计图都可以合成一个纵向复式条形统计图。
三、填空题
7.条形统计图的优点是不仅能清楚地看出数量的________,而且便于对两组数据进行________比较。
8.下图________是单式统计图.________是复式条形统计图.
9.小明骑自行车到距离家6千米的公园去玩.请你根据折线图回答:
①小明在公园玩了________分钟;
②如果路上不休息,他________?分钟到公园;
③返回时,小明骑自行车速度是每小时________千米.
10.常用的复式条形统计图有________和________两种.
11.看图填空。
观察图,使用电话投票的方式,________的票数最多,是________票,使用网络投票的方式,________的票数最少,是________票。
四、解答题
12.下面是某家电商场2019年上半年甲、乙两种品牌的冰箱销售数量情况统计图。请看图解答问题。
(1)两种品牌冰箱的销售量,在________月份相差最大。
(2)列式计算,甲种品牌的汽车,三月份的销售量比四月份少百之几?
(3)请自己提一个问题,并解答出来。
13.下面两个统计图反映的是甲、乙两位同学期末复习阶段数学自测成绩和在家学习时间的分配情况。
看图回答以下问题:
(1)从折线统计图看出________的成绩提高得快。从条形统计图看出________的反思时间少一些。
(2)甲的反思的时间占学习总时间的________,乙的反思的时间占学习总时间的________。
(3)你喜欢谁的学习方式?为什么?
14.下面是某服装厂2004年各季度生产情况统计表.
(1)根据表中数据,完成下面的统计图.
(2)根据统计图填空.
①第( ??)季度的产量最多,第( ??)季度的产量最少.
②2004年这个厂的服装总产量是( ??)箱.平均每个季度生产服装( ??)箱.
五、应用题
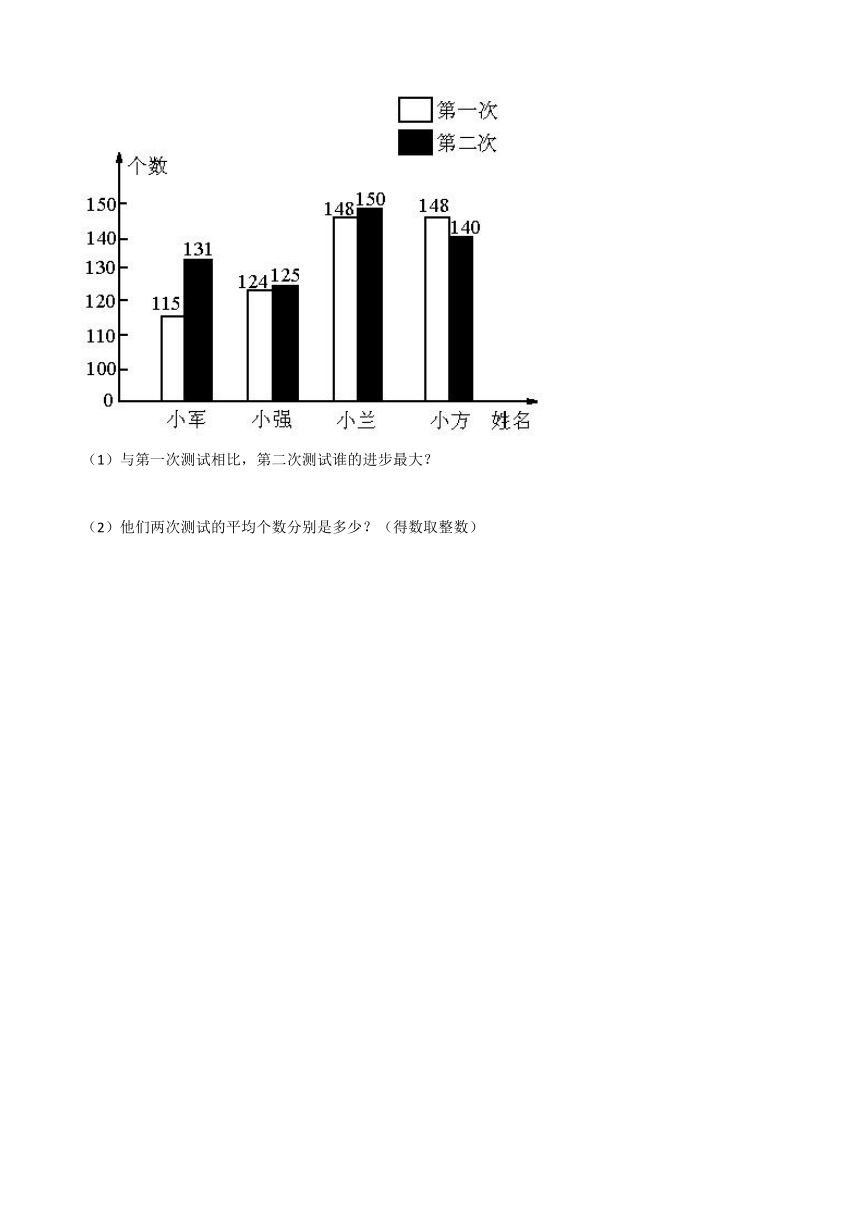
15.四一班某小组同学跳绳测试成绩如下图.
(1)与第一次测试相比,第二次测试谁的进步最大?
(2)他们两次测试的平均个数分别是多少?(得数取整数)
参考答案
一、单选题
1.【答案】 B
【解析】【解答】从图中可以看出,2001年对应的实际产量和计划产量相差最多,故选B
【分析】本题要求能读懂和会分析复式折线统计图中的数据
2.【答案】 A
【解析】
3.【答案】 B
【解析】【解答】解:选项A,甲队一共修的米数=40+50+54+56=200(米)
乙队一共修的米数=45+48+50+60=203(米)
203-200=3(米),所以乙队一共比甲队多修3米,即错误;
选项B,甲队:40<50<54<56;
乙队:45<48<50<60;
所以两队的修路速度都在加快,即正确;
选项C,第一天乙队比甲队修的多,即错误。
故答案为:B。
【分析】用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。从复式条形统计图中很容易看出两者数量的多少。
本题中根据观察出来的数据,对各个选项进行判断即可。
4.【答案】 C
【解析】【解答】由统计图的特点可知:要表示六年一班男女同学的身高情况,需要选用复式条形统计图。
【分析】条形统计图能很容易看出数量的多少,此题应根据条形统计图的特点进行解答。
二、判断题
5.【答案】错误
【解析】【解答】根据条形统计图的特点可知:条形统计图的条形可以表示两种不同的数量,可以是纵向的,也可以是横向的。【分析】条形统计图分为:单式条形统计图和复式条形统计图,前者只表示1个项目的数据,后者可以同时表示多个项目的数据;可以是纵向的,也可以是横向的。掌握条形统计图的分类和特点。
6.【答案】错误
【解析】【解答】为了便于分析和比较,有时需要把两个有联系的统计图合编成一个复式统计图,原题说法错误。【分析】为了便于分析和比较,有时需要把两个有联系的统计图合编成一个复式统计图.但不是任意两个条形统计图都可以合成一个纵向复式条形统计图。
三、填空题
7.【答案】 多少;大小
【解析】【解答】解:条形统计图的优点是不仅能清楚地看出数量的多少,而且便于对两组数据进行大小比较。
故答案为:多少;大小。
【分析】条形统计图就是用长条的长度来表示数量的多少。复式条形统计图还能对两种或两种以上的数据进行大小比较。
8.【答案】 A;B
【解析】【解答】A图中是一个直条一个直条画的,单式统计图。B图中是二个直条二个直条画的,是复式条形统计图。
?故答案为:A;B
【分析】单式条形统计图和复式条形统计图的相同点是都能让人清楚地看出数量的多少,不同点就是单式条形统计图用于比较一个物体,是一个直条一个直条画的,而复式条形统计图可以同时表示几种数据的变化情况,是把几个直条综合了起来。
9.【答案】20;40;9
【解析】【解答】解:①80﹣60=20(分钟),
答:小明在公园玩了20分钟;
②60﹣(40﹣20)
=60﹣20,
=40(分钟),
答:如果路上不休息,他40分钟可以到公园;
③返回的时间为:120﹣80=40(分钟)= (小时),
小明返回时的速度为:6÷ =9(千米),
答:小明返回时的速度是每小时9千米.
故答案为:①20,②40,③9.
【分析】①从折线统计图中可以看出在60分钟至80分钟处是小明在公园停留的时间,用(80﹣60)即可得到小明在公园玩耍的时间;②在20分钟至40分钟处属于小明中途休息的时间,可用(40﹣20)计算出小明中途休息了几分钟,然后再用去时的总时间60分钟减去休息的时间即可得到答案;③小明返回时的路程为6千米,返回的时间为(120﹣80)分钟,可根据公式路程÷时间=速度进行计算即可得到答案.此题主要考查的是如何从折线统计图中获取信息,然后再根据信息进行相应的计算即可.
10.【答案】竖式;横式
【解析】【解答】常用的复式条形统计图有竖式和横式两种。
【分析】根据常用的复式条形统计图的种类进行解答即可。
故答案为:竖式,横式.
11.【答案】尼莫;580;卡通人物;0
【解析】【解答】观察图,使用电话投票的方式,尼莫的票数最多,是580票,使用网络投票的方式,卡通人物的票数最少,是0票。
【分析】根据复式条形统计图可知,白色直条表示电话投票,阴影直条表示网络投票,统计图中的直条哪条最高表示谁的票数最多,哪条最矮表示谁的票数最少,没有直条的表示投票数为0。从复式条形统计图中获取信息并进行分析是关键。
四、解答题
12.【答案】 (1)五
(2)解: ÷200
=50÷200
=25%
答:三月份的销售量比四月份少25%。
(3)问题:乙品牌的冰箱三月份的销售量比四月份少百分之几?
÷200
=20÷200
=10%
答:乙品牌的冰箱三月份的销售量比四月份少10%。
【解析】【分析】(1)观察每个月两种冰箱的销售量,判断出哪月销售量相差最大;
(2)用两个月甲品牌销售量的差除以四月的销售量即可求出三月份比四月份少百分之几;
(3)提出一个合理的数学问题并解答即可。
13.【答案】 (1)甲;乙
(2);
(3)解:喜欢甲的学习方式。
因为甲善于反思,总结经验,学习效果好。
【解析】【解答】(1)从折线统计图看出甲的成绩提高得快。从条形统计图看出乙的反思时间少一些?。
(2)甲:3÷(5+4+3)=3÷12=
乙:2÷(5+5+2)=2÷12=
所以甲的反思的时间占学习总时间的, 乙的反思的时间占学习总时间的。
【分析】(1)直接看图解答即可;(2)反思的时间占学习总时间的几分之几=反思的时间÷学习总时间;(3)答案合理即可。
14.【答案】 (1)解:如图:
(2)解:140<180<210<230
①第(二)季度的产量最多,第(一)季度的产量最少;
140+230+180+210=760(箱),760÷4=190(箱)
②2004年这个厂的服装总产量是(760)箱.平均每个季度生产服装(190)箱.
【解析】【分析】(1)先判断横轴和竖轴表示的意义,锐角根据统计表中的数据描出对应点,再顺次连接各点即可绘制出统计图;(2)根据各个数据判断哪个季度产量最多,哪个季度产量最少;把各个季度的产量相加求出总产量,用总产量除以季度数即可求出平均每个季度的产量.
五、应用题
15.【答案】 (1)解:131-115=16(个),125-124=1(个),150-148=2(个),小方退步148-140=8(个),16最大,说明小军进步最大。
答:小军进步最大
(2)解:(115+124+148+148)÷4≈134(个)
(131+125+150+140)÷4≈137(个)
答:他们两次测试的平均个数分别是134个,137个。
【解析】【分析】(1)第二次测试成绩-第一次测试成绩=进步个数,那个数大,那个人进步就大;
(2)第一次测试的4个成绩的和÷4=第一次测试的成绩,第二次测试的4个成绩的和÷4=第二次测试的成绩。
一、单选题
1.观察下边的折线统计图,哪一年实际产量超出计划产量最多( )。
A.?1999年????????????????????????????????????B.?2001年????????????????????????????????????C.?2002年
2.下面是阳光小学和实验小学学生四到六年级近视人数统计图。根据统计情况估计一下,哪个小学的近视人数更多?
A.?阳光小学??????????????????????????????????B.?实验小学??????????????????????????????????C.?不能确定
3.甲、乙两修路队修路情况如图所示,正确的说法是(??? )
A.?甲队一共比乙队多修3米??????????B.?两队的修路速度都在加快??????????C.?甲队每天修的都比乙队多
4.要表示六年一班男女同学的身高情况,需要选用( )。
A.?条形统计图??????????????????????????B.?复式折线统计图??????????????????????????C.?复式条形统计图
二、判断题
5.纵向复式条形统计图比横向复式条形统计图表示的更明白。
6.任意两个条形统计图都可以合成一个纵向复式条形统计图。
三、填空题
7.条形统计图的优点是不仅能清楚地看出数量的________,而且便于对两组数据进行________比较。
8.下图________是单式统计图.________是复式条形统计图.
9.小明骑自行车到距离家6千米的公园去玩.请你根据折线图回答:
①小明在公园玩了________分钟;
②如果路上不休息,他________?分钟到公园;
③返回时,小明骑自行车速度是每小时________千米.
10.常用的复式条形统计图有________和________两种.
11.看图填空。
观察图,使用电话投票的方式,________的票数最多,是________票,使用网络投票的方式,________的票数最少,是________票。
四、解答题
12.下面是某家电商场2019年上半年甲、乙两种品牌的冰箱销售数量情况统计图。请看图解答问题。
(1)两种品牌冰箱的销售量,在________月份相差最大。
(2)列式计算,甲种品牌的汽车,三月份的销售量比四月份少百之几?
(3)请自己提一个问题,并解答出来。
13.下面两个统计图反映的是甲、乙两位同学期末复习阶段数学自测成绩和在家学习时间的分配情况。
看图回答以下问题:
(1)从折线统计图看出________的成绩提高得快。从条形统计图看出________的反思时间少一些。
(2)甲的反思的时间占学习总时间的________,乙的反思的时间占学习总时间的________。
(3)你喜欢谁的学习方式?为什么?
14.下面是某服装厂2004年各季度生产情况统计表.
(1)根据表中数据,完成下面的统计图.
(2)根据统计图填空.
①第( ??)季度的产量最多,第( ??)季度的产量最少.
②2004年这个厂的服装总产量是( ??)箱.平均每个季度生产服装( ??)箱.
五、应用题
15.四一班某小组同学跳绳测试成绩如下图.
(1)与第一次测试相比,第二次测试谁的进步最大?
(2)他们两次测试的平均个数分别是多少?(得数取整数)
参考答案
一、单选题
1.【答案】 B
【解析】【解答】从图中可以看出,2001年对应的实际产量和计划产量相差最多,故选B
【分析】本题要求能读懂和会分析复式折线统计图中的数据
2.【答案】 A
【解析】
3.【答案】 B
【解析】【解答】解:选项A,甲队一共修的米数=40+50+54+56=200(米)
乙队一共修的米数=45+48+50+60=203(米)
203-200=3(米),所以乙队一共比甲队多修3米,即错误;
选项B,甲队:40<50<54<56;
乙队:45<48<50<60;
所以两队的修路速度都在加快,即正确;
选项C,第一天乙队比甲队修的多,即错误。
故答案为:B。
【分析】用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。从复式条形统计图中很容易看出两者数量的多少。
本题中根据观察出来的数据,对各个选项进行判断即可。
4.【答案】 C
【解析】【解答】由统计图的特点可知:要表示六年一班男女同学的身高情况,需要选用复式条形统计图。
【分析】条形统计图能很容易看出数量的多少,此题应根据条形统计图的特点进行解答。
二、判断题
5.【答案】错误
【解析】【解答】根据条形统计图的特点可知:条形统计图的条形可以表示两种不同的数量,可以是纵向的,也可以是横向的。【分析】条形统计图分为:单式条形统计图和复式条形统计图,前者只表示1个项目的数据,后者可以同时表示多个项目的数据;可以是纵向的,也可以是横向的。掌握条形统计图的分类和特点。
6.【答案】错误
【解析】【解答】为了便于分析和比较,有时需要把两个有联系的统计图合编成一个复式统计图,原题说法错误。【分析】为了便于分析和比较,有时需要把两个有联系的统计图合编成一个复式统计图.但不是任意两个条形统计图都可以合成一个纵向复式条形统计图。
三、填空题
7.【答案】 多少;大小
【解析】【解答】解:条形统计图的优点是不仅能清楚地看出数量的多少,而且便于对两组数据进行大小比较。
故答案为:多少;大小。
【分析】条形统计图就是用长条的长度来表示数量的多少。复式条形统计图还能对两种或两种以上的数据进行大小比较。
8.【答案】 A;B
【解析】【解答】A图中是一个直条一个直条画的,单式统计图。B图中是二个直条二个直条画的,是复式条形统计图。
?故答案为:A;B
【分析】单式条形统计图和复式条形统计图的相同点是都能让人清楚地看出数量的多少,不同点就是单式条形统计图用于比较一个物体,是一个直条一个直条画的,而复式条形统计图可以同时表示几种数据的变化情况,是把几个直条综合了起来。
9.【答案】20;40;9
【解析】【解答】解:①80﹣60=20(分钟),
答:小明在公园玩了20分钟;
②60﹣(40﹣20)
=60﹣20,
=40(分钟),
答:如果路上不休息,他40分钟可以到公园;
③返回的时间为:120﹣80=40(分钟)= (小时),
小明返回时的速度为:6÷ =9(千米),
答:小明返回时的速度是每小时9千米.
故答案为:①20,②40,③9.
【分析】①从折线统计图中可以看出在60分钟至80分钟处是小明在公园停留的时间,用(80﹣60)即可得到小明在公园玩耍的时间;②在20分钟至40分钟处属于小明中途休息的时间,可用(40﹣20)计算出小明中途休息了几分钟,然后再用去时的总时间60分钟减去休息的时间即可得到答案;③小明返回时的路程为6千米,返回的时间为(120﹣80)分钟,可根据公式路程÷时间=速度进行计算即可得到答案.此题主要考查的是如何从折线统计图中获取信息,然后再根据信息进行相应的计算即可.
10.【答案】竖式;横式
【解析】【解答】常用的复式条形统计图有竖式和横式两种。
【分析】根据常用的复式条形统计图的种类进行解答即可。
故答案为:竖式,横式.
11.【答案】尼莫;580;卡通人物;0
【解析】【解答】观察图,使用电话投票的方式,尼莫的票数最多,是580票,使用网络投票的方式,卡通人物的票数最少,是0票。
【分析】根据复式条形统计图可知,白色直条表示电话投票,阴影直条表示网络投票,统计图中的直条哪条最高表示谁的票数最多,哪条最矮表示谁的票数最少,没有直条的表示投票数为0。从复式条形统计图中获取信息并进行分析是关键。
四、解答题
12.【答案】 (1)五
(2)解: ÷200
=50÷200
=25%
答:三月份的销售量比四月份少25%。
(3)问题:乙品牌的冰箱三月份的销售量比四月份少百分之几?
÷200
=20÷200
=10%
答:乙品牌的冰箱三月份的销售量比四月份少10%。
【解析】【分析】(1)观察每个月两种冰箱的销售量,判断出哪月销售量相差最大;
(2)用两个月甲品牌销售量的差除以四月的销售量即可求出三月份比四月份少百分之几;
(3)提出一个合理的数学问题并解答即可。
13.【答案】 (1)甲;乙
(2);
(3)解:喜欢甲的学习方式。
因为甲善于反思,总结经验,学习效果好。
【解析】【解答】(1)从折线统计图看出甲的成绩提高得快。从条形统计图看出乙的反思时间少一些?。
(2)甲:3÷(5+4+3)=3÷12=
乙:2÷(5+5+2)=2÷12=
所以甲的反思的时间占学习总时间的, 乙的反思的时间占学习总时间的。
【分析】(1)直接看图解答即可;(2)反思的时间占学习总时间的几分之几=反思的时间÷学习总时间;(3)答案合理即可。
14.【答案】 (1)解:如图:
(2)解:140<180<210<230
①第(二)季度的产量最多,第(一)季度的产量最少;
140+230+180+210=760(箱),760÷4=190(箱)
②2004年这个厂的服装总产量是(760)箱.平均每个季度生产服装(190)箱.
【解析】【分析】(1)先判断横轴和竖轴表示的意义,锐角根据统计表中的数据描出对应点,再顺次连接各点即可绘制出统计图;(2)根据各个数据判断哪个季度产量最多,哪个季度产量最少;把各个季度的产量相加求出总产量,用总产量除以季度数即可求出平均每个季度的产量.
五、应用题
15.【答案】 (1)解:131-115=16(个),125-124=1(个),150-148=2(个),小方退步148-140=8(个),16最大,说明小军进步最大。
答:小军进步最大
(2)解:(115+124+148+148)÷4≈134(个)
(131+125+150+140)÷4≈137(个)
答:他们两次测试的平均个数分别是134个,137个。
【解析】【分析】(1)第二次测试成绩-第一次测试成绩=进步个数,那个数大,那个人进步就大;
(2)第一次测试的4个成绩的和÷4=第一次测试的成绩,第二次测试的4个成绩的和÷4=第二次测试的成绩。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
