苏教版高中数学必修1课件 2.1.1 函数的概念和图象(3)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.1.1 函数的概念和图象(3) |  | |
| 格式 | rar | ||
| 文件大小 | 137.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 09:18:53 | ||
图片预览




文档简介
(共16张PPT)
高中数学 必修1
情境问题:
1.函数及函数定义域的概念:
一般地,设A,B是两个非空数集,如果按照某种对应法则f,对于集合A中的每个元素x,在集合B中都有惟一的元素和它对应,那么这样的对应叫从A到B的一个函数.通常记为:y=f(x),x A, x的值构成的集合A叫函数y=f(x)的定义域.
2.回忆常见函数的模型及图象:
是不是每一个函数都可以用图象表示呢?怎样才能准确地作出一个函数的图象呢?
y =2x-1
x
y
O
y
x
O
y =x2
y
x
O
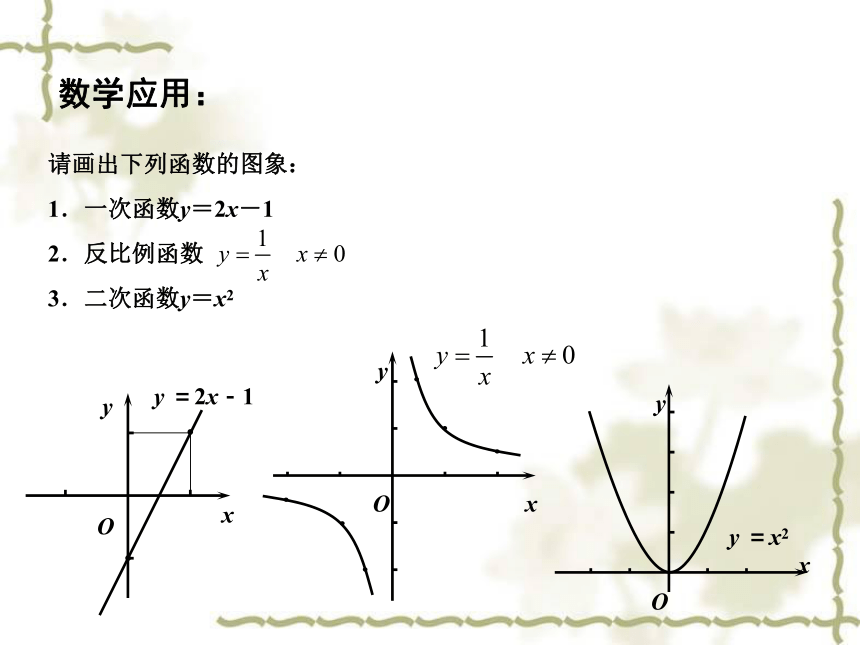
请画出下列函数的图象:
1.一次函数y=2x-1
2.反比例函数
3.二次函数y=x2
数学应用:
数学建构:
画图象,先列表,描点连线平滑好;
画直线,找两点,再用直尺把线连;
抛物线,找顶点,对称轴就很明显.
作函数的图象的基本方法:
——描点法:
函数的图象:
一般地,我们将自变量的一个值x0作为横坐标就得到坐标平面上的一个点(x0,f(x0)),自变量取遍函数定义域A的每个值时,就得到一系列这样的点,所有这些点组成的集合(点集)为{(x,y)|y=f(x),x A},这些点组成的曲线就是函数y=f(x)的图象.
例1.画出下列函数的图象;
数学应用:
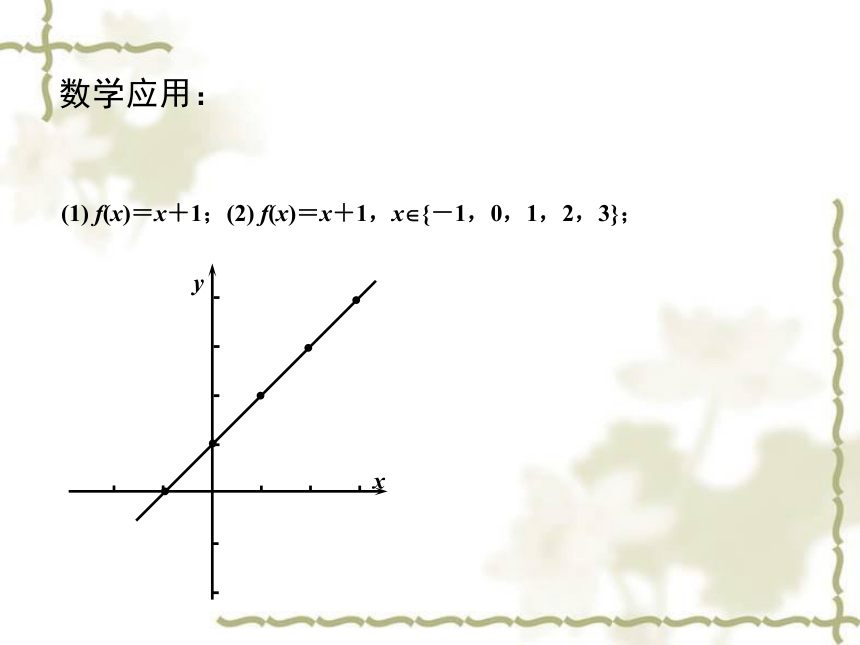
(1) f(x)=x+1; (2) f(x)=x+1,x {-1,0,1,2,3};
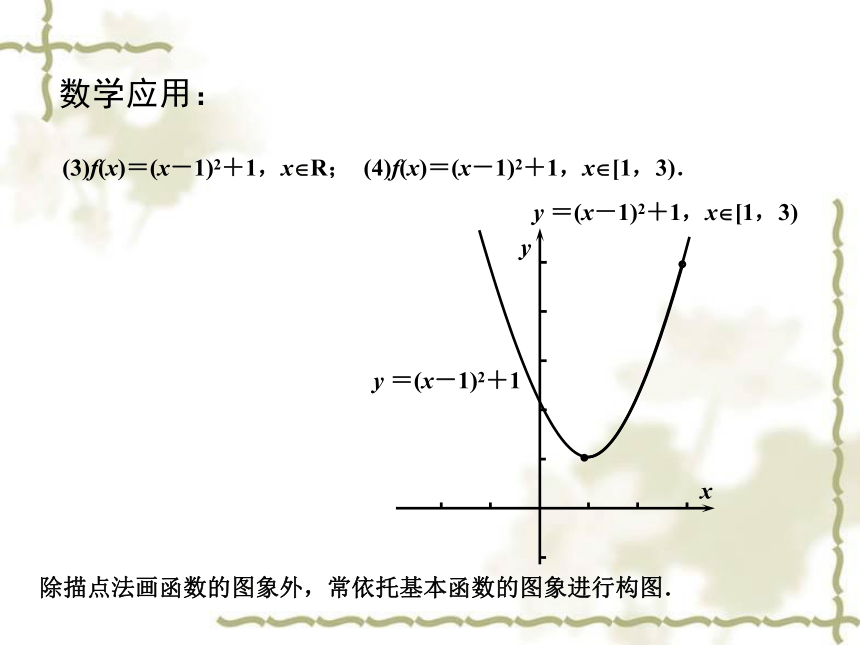
(3)f(x)=(x-1)2+1,x R; (4)f(x)=(x-1)2+1,x [1,3).
数学应用:
y
x
(1) f(x)=x+1;(2) f(x)=x+1,x {-1,0,1,2,3};
y
x
y =(x-1)2+1
数学应用:
y =(x-1)2+1,x [1,3)
除描点法画函数的图象外,常依托基本函数的图象进行构图.
(3)f(x)=(x-1)2+1,x R; (4)f(x)=(x-1)2+1,x [1,3).
例2.从人口统计年鉴中查到我国从1949年至1999年人口数据资料如下表所示:
数学应用:
把人口数y(百万人)看作是年份x的函数,试根据表中数据画出函数的图象.
年份 1949 1954 1959 1964 1969 1974 1979 1984 1989 1994 1999
人口数(百万) 542 603 672 705 807 909 975 1035 1107 1177 1246
此类图形常借助于电脑的Excel进行.
数学建构:
用Excel作图的基本步骤 :
⑴赋值
⑵命令函数
⑶进行函数运算
⑷选择“XY散点图/无数据点平滑线散点图”插入图表.
例3.画出函数f(x)=x2+1的图象,并根据图象回答下列问题:
⑴比较f(-2),f(1),f(3)的大小;
⑵若0<x1<x2,试比较f(x1)与f(x2)的大小.
y
x
y =x2+1
数学应用:
构造函数的图象,最主要是为了应用.
x1
x2
画出下列函数的图象:
(1)y=|x-1|+|x+1|;
(2)y=|x-1|-|x+1|;
数学应用:
(3)y=x|2-x|.
(1) y=|x-1|+|x+1|
数学应用:
=
-2x,x≤-1,
2,-1<x≤1,
2x,x>1.
y
x
O
(2) y=|x-1|-|x+1|
数学应用:
=
-2,x≤-1,
2x ,-1<x≤1,
2,x>1.
y
x
O
数学应用:
(3) y= x|2-x|
=
-x2+2x ,x≤2,
x2-2x,x>2.
y
x
O
小结:
描点法:
基本图象变换法:
M={(x,y) |y= f(x),x A}
函数的图象:
函数图象的构造:
平移变换
对称变换
函数图象的应用:
作业:
课本P29第3题.
高中数学 必修1
情境问题:
1.函数及函数定义域的概念:
一般地,设A,B是两个非空数集,如果按照某种对应法则f,对于集合A中的每个元素x,在集合B中都有惟一的元素和它对应,那么这样的对应叫从A到B的一个函数.通常记为:y=f(x),x A, x的值构成的集合A叫函数y=f(x)的定义域.
2.回忆常见函数的模型及图象:
是不是每一个函数都可以用图象表示呢?怎样才能准确地作出一个函数的图象呢?
y =2x-1
x
y
O
y
x
O
y =x2
y
x
O
请画出下列函数的图象:
1.一次函数y=2x-1
2.反比例函数
3.二次函数y=x2
数学应用:
数学建构:
画图象,先列表,描点连线平滑好;
画直线,找两点,再用直尺把线连;
抛物线,找顶点,对称轴就很明显.
作函数的图象的基本方法:
——描点法:
函数的图象:
一般地,我们将自变量的一个值x0作为横坐标就得到坐标平面上的一个点(x0,f(x0)),自变量取遍函数定义域A的每个值时,就得到一系列这样的点,所有这些点组成的集合(点集)为{(x,y)|y=f(x),x A},这些点组成的曲线就是函数y=f(x)的图象.
例1.画出下列函数的图象;
数学应用:
(1) f(x)=x+1; (2) f(x)=x+1,x {-1,0,1,2,3};
(3)f(x)=(x-1)2+1,x R; (4)f(x)=(x-1)2+1,x [1,3).
数学应用:
y
x
(1) f(x)=x+1;(2) f(x)=x+1,x {-1,0,1,2,3};
y
x
y =(x-1)2+1
数学应用:
y =(x-1)2+1,x [1,3)
除描点法画函数的图象外,常依托基本函数的图象进行构图.
(3)f(x)=(x-1)2+1,x R; (4)f(x)=(x-1)2+1,x [1,3).
例2.从人口统计年鉴中查到我国从1949年至1999年人口数据资料如下表所示:
数学应用:
把人口数y(百万人)看作是年份x的函数,试根据表中数据画出函数的图象.
年份 1949 1954 1959 1964 1969 1974 1979 1984 1989 1994 1999
人口数(百万) 542 603 672 705 807 909 975 1035 1107 1177 1246
此类图形常借助于电脑的Excel进行.
数学建构:
用Excel作图的基本步骤 :
⑴赋值
⑵命令函数
⑶进行函数运算
⑷选择“XY散点图/无数据点平滑线散点图”插入图表.
例3.画出函数f(x)=x2+1的图象,并根据图象回答下列问题:
⑴比较f(-2),f(1),f(3)的大小;
⑵若0<x1<x2,试比较f(x1)与f(x2)的大小.
y
x
y =x2+1
数学应用:
构造函数的图象,最主要是为了应用.
x1
x2
画出下列函数的图象:
(1)y=|x-1|+|x+1|;
(2)y=|x-1|-|x+1|;
数学应用:
(3)y=x|2-x|.
(1) y=|x-1|+|x+1|
数学应用:
=
-2x,x≤-1,
2,-1<x≤1,
2x,x>1.
y
x
O
(2) y=|x-1|-|x+1|
数学应用:
=
-2,x≤-1,
2x ,-1<x≤1,
2,x>1.
y
x
O
数学应用:
(3) y= x|2-x|
=
-x2+2x ,x≤2,
x2-2x,x>2.
y
x
O
小结:
描点法:
基本图象变换法:
M={(x,y) |y= f(x),x A}
函数的图象:
函数图象的构造:
平移变换
对称变换
函数图象的应用:
作业:
课本P29第3题.
