苏教版高中数学必修1课件 2.1.2 函数的表示方法(1)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.1.2 函数的表示方法(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 136.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
高中数学 必修1
情境问题:
定义域
值域
A={x|y= f(x)}
C={y|y= f(x),x A}
M={(x,y)|y= f(x),x A}
函数的图象
函数的三要素
函数存在的范围
函数本质属性的直观反映
函数变化的范围
下表的对应关系能否表示一个函数呢?
x 1 3 5 7
y -1 -3 0 0
1.1 n mile(海里)约为1854m,根据这一关系,写出米数y关于海里数x的函数解析式.
2.用长为30cm的铁丝围成矩形,试将矩形的面积S(cm2)表示为矩形一边长x(cm)的函数,并画出函数的图象.
数学应用:
数学应用:
例1.购买某种饮料x听,所需钱数为y元.若每听2元,试分别用解析法、列表法、图象法将y表示成x(x {1,2,3,4})的函数,并指出该函数的值域.
解析法
y=2x
(x {1,2,3,4})
x 1 2 3 4
y
2
4
6
8
y
x
O
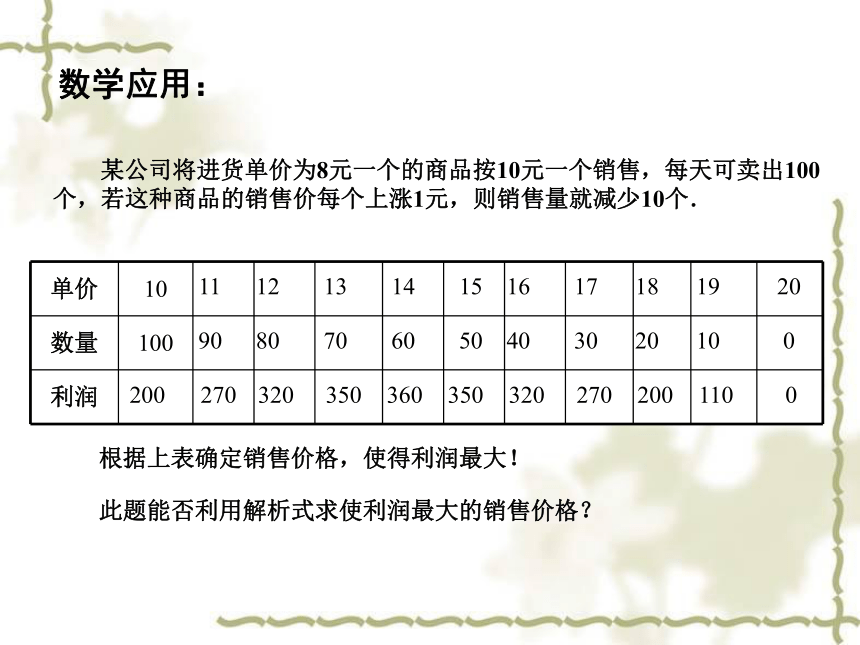
某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个.
单价 10
数量 100
利润
200
11
90
270
12
80
320
13
70
350
14
60
360
15
50
350
16
40
320
17
30
270
18
20
200
19
10
110
20
0
0
根据上表确定销售价格,使得利润最大!
此题能否利用解析式求使利润最大的销售价格?
数学应用:
对应关系清晰明了
直观而形象
简单便于研究
不连续、容量小
对应关系不清晰
抽象
数学建构:
表示法
列表法
图象法
解析法
优点
缺点
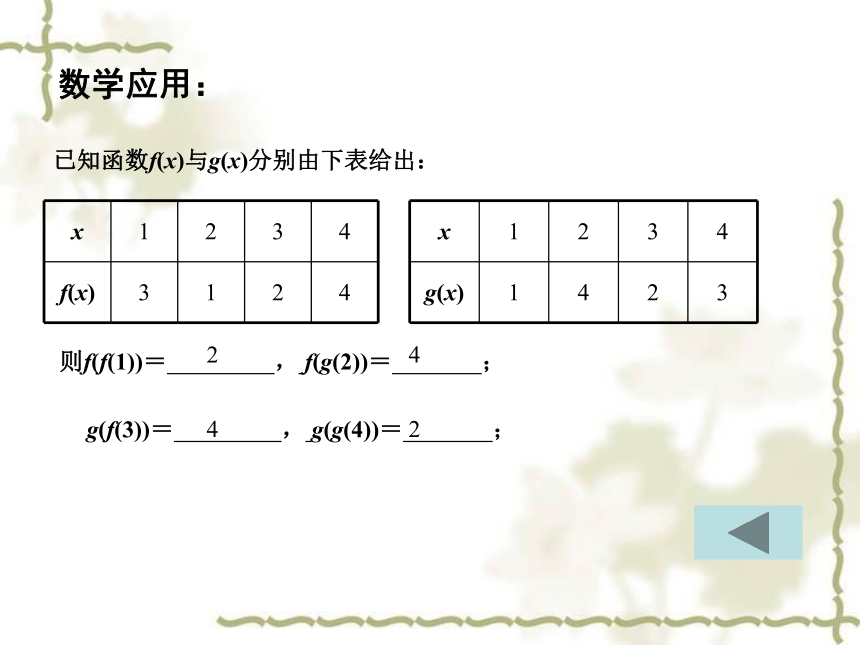
已知函数f(x)与g(x)分别由下表给出:
x 1 2 3 4
f(x) 3 1 2 4
x 1 2 3 4
g(x) 1 4 2 3
则f(f(1))= , f(g(2))= ;
g(f(3))= , g(g(4))= ;
2
4
4
2
数学应用:
例2.如图,是一个二次函数的图象的一部分,试根据图象中的有关数据,求出函数f(x)的解析式及其定义域.
数学应用:
y
x
O
数学应用:
3.已知f(x)是一次函数,且图象经过(1,0)和(-2,3)两点,求f(x)的解析式.
4.已知f(x)是一次函数,且f(f(x))=9x-4,求f(x)的解析式.
*5.已知f(x)是二次函数,且f(x+1)-x-1= f(x),且f(0)=0,求f(x).
数学建构:
已知函数模型求函数的解析式:
待定系数法求解.
(1)设出函数的解析式;
(2)建立有关参数的方程或方程组;
(3)解方程(组)得参数的值;
(4)求出函数的解析式.
6.设 f(x)=2x+3,g(x)= f(x+1),求g(x).
7.已知函数f(x+1)=x2-2x,求f(x).
数学应用:
数学建构:
已知f(x+a)求函数f(x)的解析式:
(1)凑配;
(2)换元f(x+a) f(t)(t=x+a);
注:用这两种方法求函数解析式时,需要注明自变量x的取值范围.
1.函数的表示方法.
2.不同表示法的优缺点.
小结:
3.求函数的解析式y=f(x)
待定系数法
换元法
凑配法
分类讨论法
P32第1,4,5题.
作业:
高中数学 必修1
情境问题:
定义域
值域
A={x|y= f(x)}
C={y|y= f(x),x A}
M={(x,y)|y= f(x),x A}
函数的图象
函数的三要素
函数存在的范围
函数本质属性的直观反映
函数变化的范围
下表的对应关系能否表示一个函数呢?
x 1 3 5 7
y -1 -3 0 0
1.1 n mile(海里)约为1854m,根据这一关系,写出米数y关于海里数x的函数解析式.
2.用长为30cm的铁丝围成矩形,试将矩形的面积S(cm2)表示为矩形一边长x(cm)的函数,并画出函数的图象.
数学应用:
数学应用:
例1.购买某种饮料x听,所需钱数为y元.若每听2元,试分别用解析法、列表法、图象法将y表示成x(x {1,2,3,4})的函数,并指出该函数的值域.
解析法
y=2x
(x {1,2,3,4})
x 1 2 3 4
y
2
4
6
8
y
x
O
某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个.
单价 10
数量 100
利润
200
11
90
270
12
80
320
13
70
350
14
60
360
15
50
350
16
40
320
17
30
270
18
20
200
19
10
110
20
0
0
根据上表确定销售价格,使得利润最大!
此题能否利用解析式求使利润最大的销售价格?
数学应用:
对应关系清晰明了
直观而形象
简单便于研究
不连续、容量小
对应关系不清晰
抽象
数学建构:
表示法
列表法
图象法
解析法
优点
缺点
已知函数f(x)与g(x)分别由下表给出:
x 1 2 3 4
f(x) 3 1 2 4
x 1 2 3 4
g(x) 1 4 2 3
则f(f(1))= , f(g(2))= ;
g(f(3))= , g(g(4))= ;
2
4
4
2
数学应用:
例2.如图,是一个二次函数的图象的一部分,试根据图象中的有关数据,求出函数f(x)的解析式及其定义域.
数学应用:
y
x
O
数学应用:
3.已知f(x)是一次函数,且图象经过(1,0)和(-2,3)两点,求f(x)的解析式.
4.已知f(x)是一次函数,且f(f(x))=9x-4,求f(x)的解析式.
*5.已知f(x)是二次函数,且f(x+1)-x-1= f(x),且f(0)=0,求f(x).
数学建构:
已知函数模型求函数的解析式:
待定系数法求解.
(1)设出函数的解析式;
(2)建立有关参数的方程或方程组;
(3)解方程(组)得参数的值;
(4)求出函数的解析式.
6.设 f(x)=2x+3,g(x)= f(x+1),求g(x).
7.已知函数f(x+1)=x2-2x,求f(x).
数学应用:
数学建构:
已知f(x+a)求函数f(x)的解析式:
(1)凑配;
(2)换元f(x+a) f(t)(t=x+a);
注:用这两种方法求函数解析式时,需要注明自变量x的取值范围.
1.函数的表示方法.
2.不同表示法的优缺点.
小结:
3.求函数的解析式y=f(x)
待定系数法
换元法
凑配法
分类讨论法
P32第1,4,5题.
作业:
