苏教版高中数学必修1课件 2.1.2 函数的表示方法(2)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.1.2 函数的表示方法(2) |  | |
| 格式 | rar | ||
| 文件大小 | 116.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 09:18:53 | ||
图片预览



文档简介
(共11张PPT)
高中数学 必修1
情境问题:
列表法
解析法
图象法
函数的表示法
如果函数y=f(x) 在不同的区间上具有不同的对应法则呢
例1.某市出租汽车收费标准如下:在3km以内(含3km)路程按起步价7元收费,超过3km以外的路程按2.4元/km收费.试写出收费额关于路程的函数解析式.
数学应用:
实际问题中,分段函数是常见的函数模型.
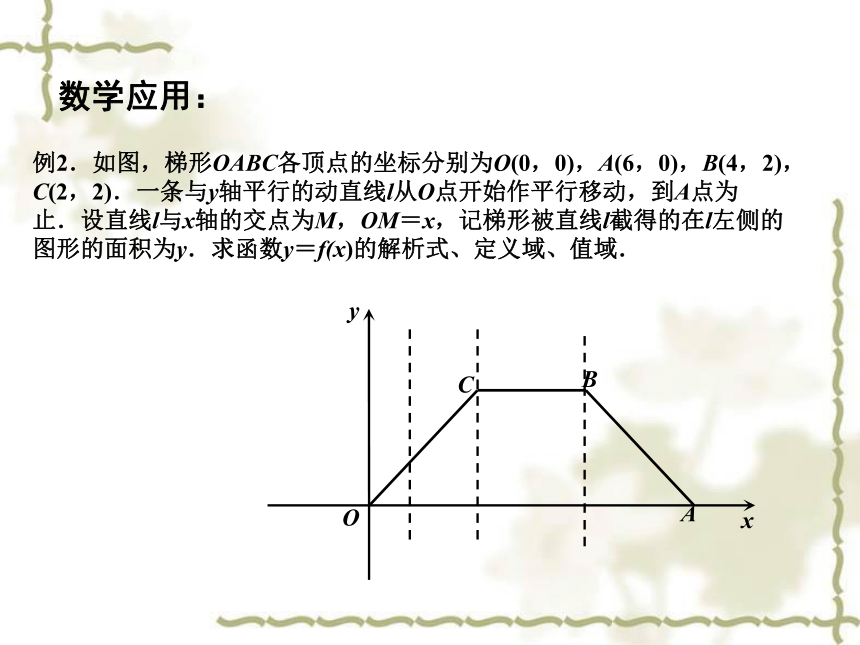
例2.如图,梯形OABC各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始作平行移动,到A点为止.设直线l与x轴的交点为M,OM=x,记梯形被直线l截得的在l左侧的图形的面积为y.求函数y=f(x)的解析式、定义域、值域.
x
y
O
A
B
C
数学应用:
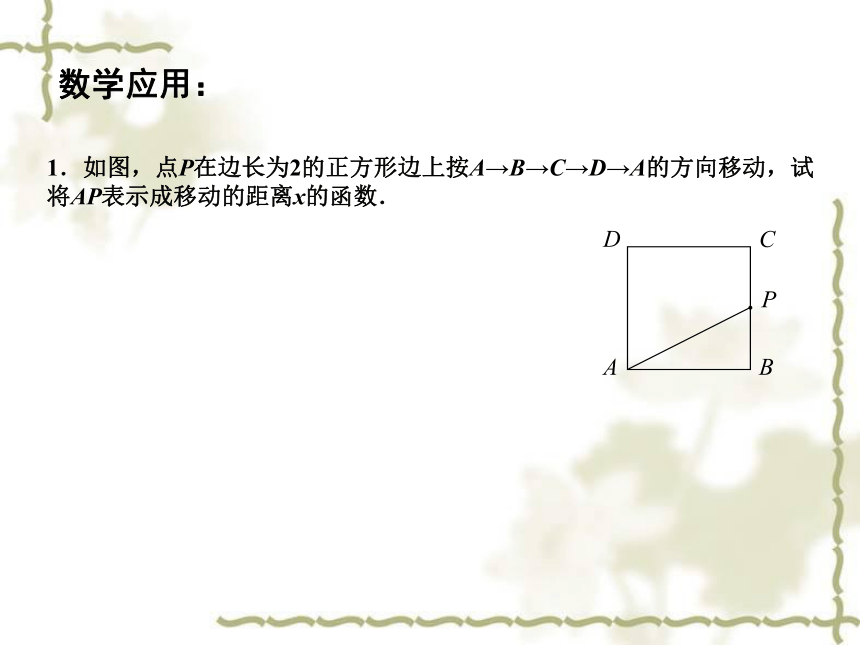
1.如图,点P在边长为2的正方形边上按A→B→C→D→A的方向移动,试将AP表示成移动的距离x的函数.
数学应用:
A
B
C
D
P
例3.将函数f(x)= | x+1|+| x-2|表示成分段函数的形式,并画出其图象,根据图象指出函数f(x)的值域.
数学应用:
f (x)=
2x-1
x≥2
-2x+1
x<-1
3
-1≤x<2
y
x
O
f (x)
2.函数f(x)=| 2x+1|与g(x)=| x+1| +| x| 是同一函数吗?
画出函数f(x)与g(x)的图象.
x -3 -2 -1 0 1 2 3
f(x) 5 3 1 1 3 5 7
g(x) 5 3 1 1 3 5 7
数学应用:
列表对比:
f(x)=| 2x+1|
f(x)=
2x+1,
x≥-0.5
-2x-1,
x<-0.5
g(x)=
2x+1
x≥0
-2x-1
x<-1
1
-1≤x<0
y
x
O
y
x
O
g(x)=| x+1| +| x|
数学应用:
3.若f(x)= 求f(-1),f(0),f(2),f(f(-1)),f(f(0)),f(f(0.5))的值.
数学应用:
x2-1,x≥0,
2x+1,x<0.
小结:
2.分段函数的应用 .
1.分段函数与分类讨论.
注:分段函数不是几个函数,而是一个完整的函数,只是在不同的区间上具有不同的对应关系.
作业:
P32第3,10,12题.
高中数学 必修1
情境问题:
列表法
解析法
图象法
函数的表示法
如果函数y=f(x) 在不同的区间上具有不同的对应法则呢
例1.某市出租汽车收费标准如下:在3km以内(含3km)路程按起步价7元收费,超过3km以外的路程按2.4元/km收费.试写出收费额关于路程的函数解析式.
数学应用:
实际问题中,分段函数是常见的函数模型.
例2.如图,梯形OABC各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始作平行移动,到A点为止.设直线l与x轴的交点为M,OM=x,记梯形被直线l截得的在l左侧的图形的面积为y.求函数y=f(x)的解析式、定义域、值域.
x
y
O
A
B
C
数学应用:
1.如图,点P在边长为2的正方形边上按A→B→C→D→A的方向移动,试将AP表示成移动的距离x的函数.
数学应用:
A
B
C
D
P
例3.将函数f(x)= | x+1|+| x-2|表示成分段函数的形式,并画出其图象,根据图象指出函数f(x)的值域.
数学应用:
f (x)=
2x-1
x≥2
-2x+1
x<-1
3
-1≤x<2
y
x
O
f (x)
2.函数f(x)=| 2x+1|与g(x)=| x+1| +| x| 是同一函数吗?
画出函数f(x)与g(x)的图象.
x -3 -2 -1 0 1 2 3
f(x) 5 3 1 1 3 5 7
g(x) 5 3 1 1 3 5 7
数学应用:
列表对比:
f(x)=| 2x+1|
f(x)=
2x+1,
x≥-0.5
-2x-1,
x<-0.5
g(x)=
2x+1
x≥0
-2x-1
x<-1
1
-1≤x<0
y
x
O
y
x
O
g(x)=| x+1| +| x|
数学应用:
3.若f(x)= 求f(-1),f(0),f(2),f(f(-1)),f(f(0)),f(f(0.5))的值.
数学应用:
x2-1,x≥0,
2x+1,x<0.
小结:
2.分段函数的应用 .
1.分段函数与分类讨论.
注:分段函数不是几个函数,而是一个完整的函数,只是在不同的区间上具有不同的对应关系.
作业:
P32第3,10,12题.
