苏教版高中数学必修1课件 2.1.3 函数的简单性质(1)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.1.3 函数的简单性质(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 00:00:00 | ||
图片预览



文档简介
(共12张PPT)
高中数学 必修1
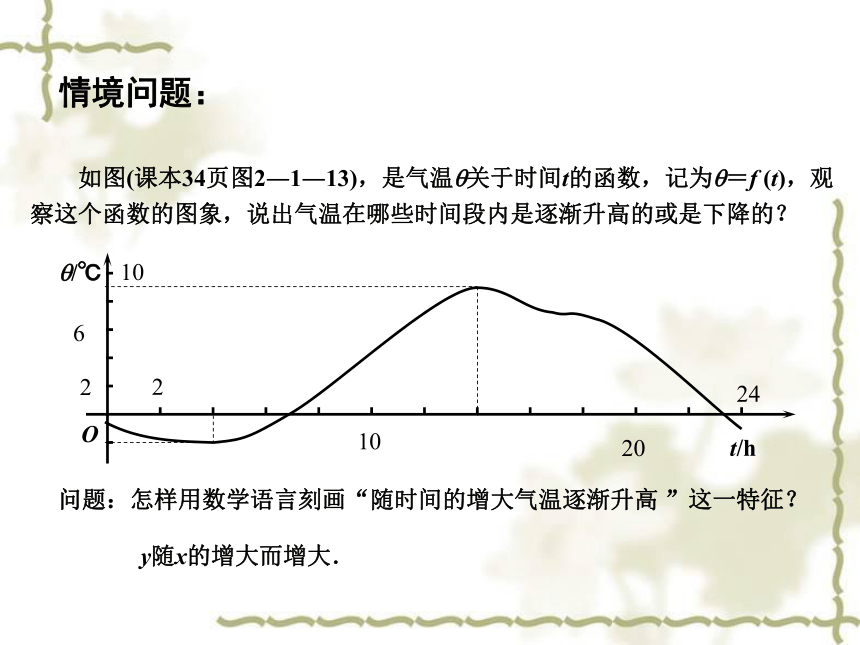
如图(课本34页图2―1―13),是气温 关于时间t的函数,记为 =f (t),观察这个函数的图象,说出气温在哪些时间段内是逐渐升高的或是下降的?
问题:怎样用数学语言刻画“随时间的增大气温逐渐升高 ”这一特征?
y随x的增大而增大.
情境问题:
t/h
/℃
O
2
2
6
10
24
20
10
(x≥0 )
在一碗水中,加入一定量的盐,盐加得越多就越咸.设水的质量为1,盐的质量为x,盐水的浓度为y,则y与x之间的函数关系是 y= .
问题一:怎样用数学语言刻画“盐加得越多就越咸”这一特征?
问题二:函数的解析式能反映出这个特征吗?
y随x的增大而增大.
情境问题:
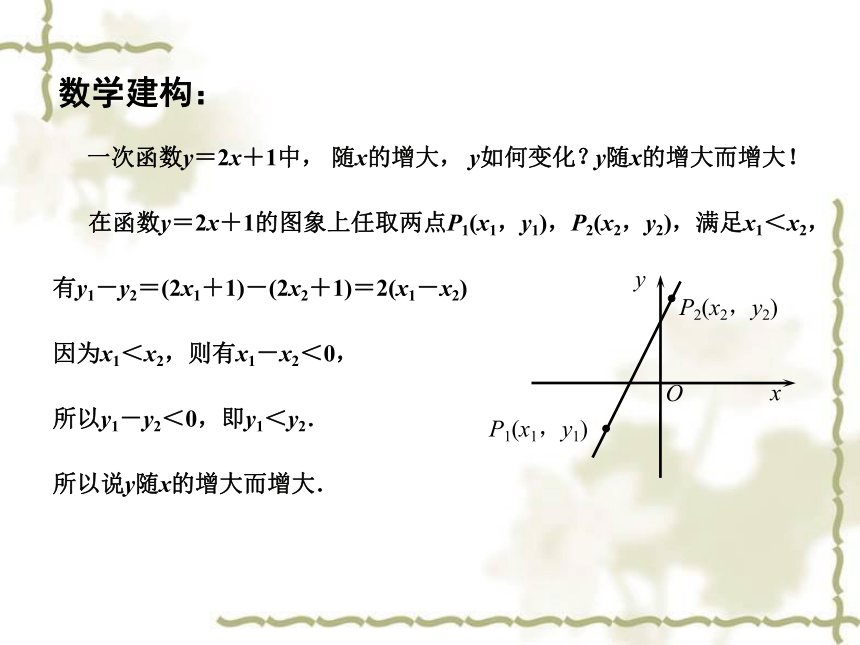
一次函数y=2x+1中, 随x的增大, y如何变化?
y随x的增大而增大!
数学建构:
x
y
O
P1(x1,y1)
P2(x2,y2)
在函数y=2x+1的图象上任取两点P1(x1,y1),P2(x2,y2),满足x1<x2,
有y1-y2=(2x1+1)-(2x2+1)=2(x1-x2)
因为x1<x2,则有x1-x2<0,
所以y1-y2<0,即y1<y2.
所以说y随x的增大而增大.
数学建构:
一般地,设函数y=f(x)的定义域为A,区间I A.
如果对于区间I内的任意两个值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说y=f(x)在区间I上是单调增函数, I称为y=f(x)的单调增区间.
如果对于区间I内的任意两个值x1,x2,当x1<x2时,都有f(x1)>f(x2),
那么就说y=f(x)在区间I上是单调减函数, I称为y=f(x)的单调减区间.
如果函数y=f(x)在区间I上是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有单调性.单调增区间和单调减区间统称为单调区间.
数学应用:
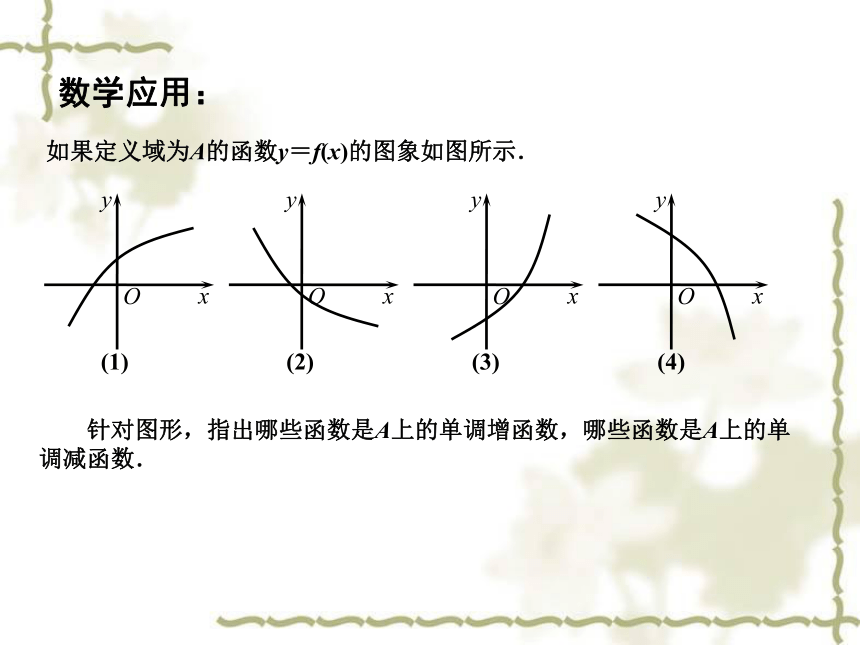
如果定义域为A的函数y=f(x)的图象如图所示.
针对图形,指出哪些函数是A上的单调增函数,哪些函数是A上的单调减函数.
x
y
O
x
y
O
x
y
O
x
y
O
(1)
(2)
(3)
(4)
数学应用:
x
y
O
表述二次函数y=x2+2x-1的单调性:
在对称轴的左侧,y随x的增大而减小,
在对称轴的右侧,y随x的增大而增大.
在区间(- ,-1)上单调递减,在区间(-1,+ )上递增.
在区间(- ,-1)上是减函数,在区间(-1,+ )上是增函数.
二次函数y=x2+2x-1的减区间是(- ,-1),增区间是(-1,+ ).
x
y
O
表述反比例函数y= 的单调性:
在第一象限,y随x的增大而减小,
在第三象限,y随x的增大而减小.
在区间(0,+ )上单调递减,在区间(- ,0)上也单调递减.
数学应用:
在区间(0,+ )上是减函数,在区间(- ,0)上也是减函数.
函数y= 的减区间是(- ,0)和(0,+ ).
注:函数y= 的减区间不能表示为(- ,0)∪(0,+ ).
(1)y=-x2+2;
例1.说出下列函数的单调区间:
(2)y= +1 (x≠0) .
解:
(1)函数y=-x2+2的增区间为(- ,0],减区间为(0,+ ).
(2)函数y= +1的单调减区间为(- ,0)和(0,+ ).
数学应用:
(1)证明:函数y=-x2+2在区间(- ,0]上单调递增;
例2.完成下列证明:
(2)证明:函数y= +1在区间为(- ,0)上单调递减.
数学应用:
(1)单调性是函数的本质属性,可根据图象写出判定函数的单调性;
(2)根据已知函数的单调性判定相关函数的单调性
(3)写单调区间时,注意区间的端点;
(4)将y=f(x)的图象上下平移时,单调区间不发生改变;左右平移时,
单调区间相应平移;
(5)单调区间不能随便求并集.
小结:
作业:
P43第2,7题.
高中数学 必修1
如图(课本34页图2―1―13),是气温 关于时间t的函数,记为 =f (t),观察这个函数的图象,说出气温在哪些时间段内是逐渐升高的或是下降的?
问题:怎样用数学语言刻画“随时间的增大气温逐渐升高 ”这一特征?
y随x的增大而增大.
情境问题:
t/h
/℃
O
2
2
6
10
24
20
10
(x≥0 )
在一碗水中,加入一定量的盐,盐加得越多就越咸.设水的质量为1,盐的质量为x,盐水的浓度为y,则y与x之间的函数关系是 y= .
问题一:怎样用数学语言刻画“盐加得越多就越咸”这一特征?
问题二:函数的解析式能反映出这个特征吗?
y随x的增大而增大.
情境问题:
一次函数y=2x+1中, 随x的增大, y如何变化?
y随x的增大而增大!
数学建构:
x
y
O
P1(x1,y1)
P2(x2,y2)
在函数y=2x+1的图象上任取两点P1(x1,y1),P2(x2,y2),满足x1<x2,
有y1-y2=(2x1+1)-(2x2+1)=2(x1-x2)
因为x1<x2,则有x1-x2<0,
所以y1-y2<0,即y1<y2.
所以说y随x的增大而增大.
数学建构:
一般地,设函数y=f(x)的定义域为A,区间I A.
如果对于区间I内的任意两个值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说y=f(x)在区间I上是单调增函数, I称为y=f(x)的单调增区间.
如果对于区间I内的任意两个值x1,x2,当x1<x2时,都有f(x1)>f(x2),
那么就说y=f(x)在区间I上是单调减函数, I称为y=f(x)的单调减区间.
如果函数y=f(x)在区间I上是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有单调性.单调增区间和单调减区间统称为单调区间.
数学应用:
如果定义域为A的函数y=f(x)的图象如图所示.
针对图形,指出哪些函数是A上的单调增函数,哪些函数是A上的单调减函数.
x
y
O
x
y
O
x
y
O
x
y
O
(1)
(2)
(3)
(4)
数学应用:
x
y
O
表述二次函数y=x2+2x-1的单调性:
在对称轴的左侧,y随x的增大而减小,
在对称轴的右侧,y随x的增大而增大.
在区间(- ,-1)上单调递减,在区间(-1,+ )上递增.
在区间(- ,-1)上是减函数,在区间(-1,+ )上是增函数.
二次函数y=x2+2x-1的减区间是(- ,-1),增区间是(-1,+ ).
x
y
O
表述反比例函数y= 的单调性:
在第一象限,y随x的增大而减小,
在第三象限,y随x的增大而减小.
在区间(0,+ )上单调递减,在区间(- ,0)上也单调递减.
数学应用:
在区间(0,+ )上是减函数,在区间(- ,0)上也是减函数.
函数y= 的减区间是(- ,0)和(0,+ ).
注:函数y= 的减区间不能表示为(- ,0)∪(0,+ ).
(1)y=-x2+2;
例1.说出下列函数的单调区间:
(2)y= +1 (x≠0) .
解:
(1)函数y=-x2+2的增区间为(- ,0],减区间为(0,+ ).
(2)函数y= +1的单调减区间为(- ,0)和(0,+ ).
数学应用:
(1)证明:函数y=-x2+2在区间(- ,0]上单调递增;
例2.完成下列证明:
(2)证明:函数y= +1在区间为(- ,0)上单调递减.
数学应用:
(1)单调性是函数的本质属性,可根据图象写出判定函数的单调性;
(2)根据已知函数的单调性判定相关函数的单调性
(3)写单调区间时,注意区间的端点;
(4)将y=f(x)的图象上下平移时,单调区间不发生改变;左右平移时,
单调区间相应平移;
(5)单调区间不能随便求并集.
小结:
作业:
P43第2,7题.
