苏教版高中数学必修1课件 2.1.3 函数的简单性质(2)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.1.3 函数的简单性质(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 113.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
高中数学 必修1
情境问题:
复述函数单调性的定义.
上节课,我们利用下图(课本34页图2-1-13)认知了函数的单调性,该天气温的变化范围是什么呢?
最高气温为9℃,在14时取得;最低气温为-2℃,在4时取得;
该天气温的变化范围为[-2,9].
情境问题:
t/h
/℃
O
2
2
6
10
24
20
10
数学建构:
一般地,设y=f(x)的定义域为A.若存在定值x0∈A,使得对任意
x∈A, f(x)≤f(x0)恒成立,则称f(x0)为y = f(x)的最大值,记为ymax= f(x0).
此时,在图象上,(x0,f(x0))是函数图象的最高点.
若存在定值x0∈A,使得对任意x∈A,f(x)≥f(x0)恒成立,则称f(x0)
为y = f(x)的最小值,记为ymin= f(x0).
此时,在图象上,(x0,f(x0))是函数图象的最低点.
例1.求下列函数的最小值.
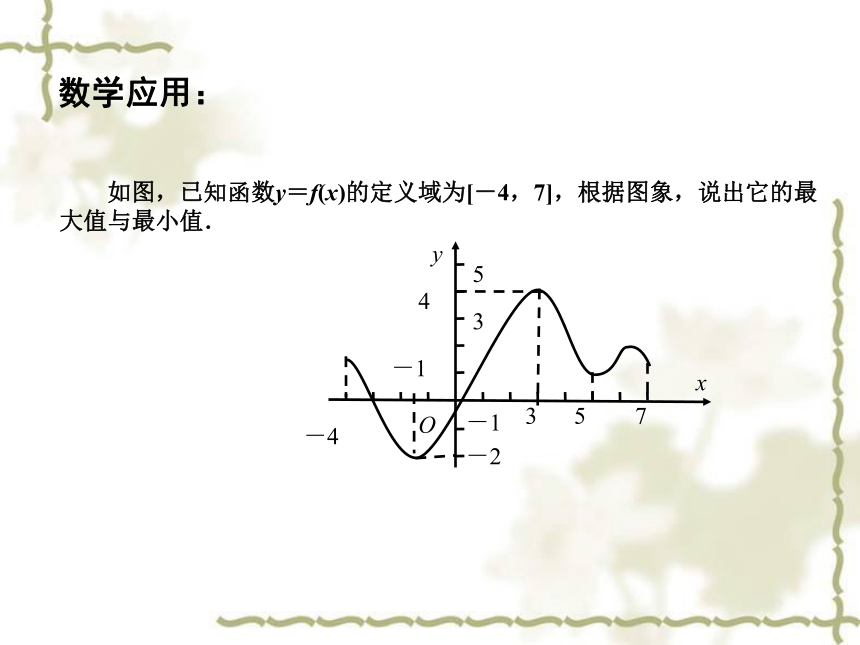
数学应用:
二次函数的最值;
求f(x)=-x2+2x在[0,10]上的最大值和最小值.
不间断函数y=f(x)在闭区间上必有最大值与最小值.
(1) f(x) =-x2+2x,x R; (2) g(x) = ,x [1,3].
3
-1
-4
x
4
3
5
5
7
-1
-2
y
O
如图,已知函数y=f(x)的定义域为[-4,7],根据图象,说出它的最大值与最小值.
数学应用:
例2.已知函数y=f(x)的定义域是[a,b],a<c<b.当x∈[a,c]时,f(x)是单调增函数;当x∈[c,b] 时,f(x)是单调减函数.试证明:
f(x)在x=c时取得最大值.
x
y
O
a
b
c
数学应用:
例2.已知函数y=f(x)的定义域是[a,b],a<c<b.当x∈[a,c]时,f(x)是单调增函数;当x∈[c,b] 时,f(x)是单调减函数.试证明:
f(x)在x=c时取得最大值.
x
y
O
a
b
c
数学应用:
变式:已知函数y=f(x)的定义域是[a,b],a<c<b.当x∈[a,c]时,f(x)是单调减函数;当x∈[c,b] 时,f(x)是单调增函数.试证明:f(x)在x=c时取得最小值.
x
y
O
a
b
c
数学应用:
1.函数y= (x∈[0,3])的值域为__________.
2.函数y= (x∈[2,6])的值域为__________.
3.函数y= (x∈(- ,-2])的值域为_________.
4.函数y= 的值域为__________.
5.函数y= 的值域为__________.
数学应用:
例3.求函数f (x)=x2-2ax在[0,4]上的最小值.
数学应用:
解:f (x)=x2-2ax=(x-a)2-a2.
(1)当a≤0时,f (x)在区间[0,4]上单调递增,
f (x)min= f (0)=0.
(2)当0<a<4时,当且仅当x =a时,f (x)取得最小值,
f (x)min= f (a)=-a2.
(3)当a≥4时,f (x)在区间[0,4]上单调递减,
f (x)min= f (4)= 16-8a .
记f (x)在区间[0,4]上的最小值为g (a) ,则
g (a)=
0, a≤0,
-a2, 0<a<4,
16-8a ,a≥4 .
单调性
最值
值域
小结:
作业:
课本37页第3题,43页第3题.
补充:已知二次函数f(x)=ax2+2ax+1在[-3,2]上有最大值4,求实数a的值.
高中数学 必修1
情境问题:
复述函数单调性的定义.
上节课,我们利用下图(课本34页图2-1-13)认知了函数的单调性,该天气温的变化范围是什么呢?
最高气温为9℃,在14时取得;最低气温为-2℃,在4时取得;
该天气温的变化范围为[-2,9].
情境问题:
t/h
/℃
O
2
2
6
10
24
20
10
数学建构:
一般地,设y=f(x)的定义域为A.若存在定值x0∈A,使得对任意
x∈A, f(x)≤f(x0)恒成立,则称f(x0)为y = f(x)的最大值,记为ymax= f(x0).
此时,在图象上,(x0,f(x0))是函数图象的最高点.
若存在定值x0∈A,使得对任意x∈A,f(x)≥f(x0)恒成立,则称f(x0)
为y = f(x)的最小值,记为ymin= f(x0).
此时,在图象上,(x0,f(x0))是函数图象的最低点.
例1.求下列函数的最小值.
数学应用:
二次函数的最值;
求f(x)=-x2+2x在[0,10]上的最大值和最小值.
不间断函数y=f(x)在闭区间上必有最大值与最小值.
(1) f(x) =-x2+2x,x R; (2) g(x) = ,x [1,3].
3
-1
-4
x
4
3
5
5
7
-1
-2
y
O
如图,已知函数y=f(x)的定义域为[-4,7],根据图象,说出它的最大值与最小值.
数学应用:
例2.已知函数y=f(x)的定义域是[a,b],a<c<b.当x∈[a,c]时,f(x)是单调增函数;当x∈[c,b] 时,f(x)是单调减函数.试证明:
f(x)在x=c时取得最大值.
x
y
O
a
b
c
数学应用:
例2.已知函数y=f(x)的定义域是[a,b],a<c<b.当x∈[a,c]时,f(x)是单调增函数;当x∈[c,b] 时,f(x)是单调减函数.试证明:
f(x)在x=c时取得最大值.
x
y
O
a
b
c
数学应用:
变式:已知函数y=f(x)的定义域是[a,b],a<c<b.当x∈[a,c]时,f(x)是单调减函数;当x∈[c,b] 时,f(x)是单调增函数.试证明:f(x)在x=c时取得最小值.
x
y
O
a
b
c
数学应用:
1.函数y= (x∈[0,3])的值域为__________.
2.函数y= (x∈[2,6])的值域为__________.
3.函数y= (x∈(- ,-2])的值域为_________.
4.函数y= 的值域为__________.
5.函数y= 的值域为__________.
数学应用:
例3.求函数f (x)=x2-2ax在[0,4]上的最小值.
数学应用:
解:f (x)=x2-2ax=(x-a)2-a2.
(1)当a≤0时,f (x)在区间[0,4]上单调递增,
f (x)min= f (0)=0.
(2)当0<a<4时,当且仅当x =a时,f (x)取得最小值,
f (x)min= f (a)=-a2.
(3)当a≥4时,f (x)在区间[0,4]上单调递减,
f (x)min= f (4)= 16-8a .
记f (x)在区间[0,4]上的最小值为g (a) ,则
g (a)=
0, a≤0,
-a2, 0<a<4,
16-8a ,a≥4 .
单调性
最值
值域
小结:
作业:
课本37页第3题,43页第3题.
补充:已知二次函数f(x)=ax2+2ax+1在[-3,2]上有最大值4,求实数a的值.
