苏教版高中数学必修1课件 2.1.3 函数的简单性质(3)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.1.3 函数的简单性质(3) |

|
|
| 格式 | rar | ||
| 文件大小 | 138.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
高中数学 必修1
复习回顾与情境创设:
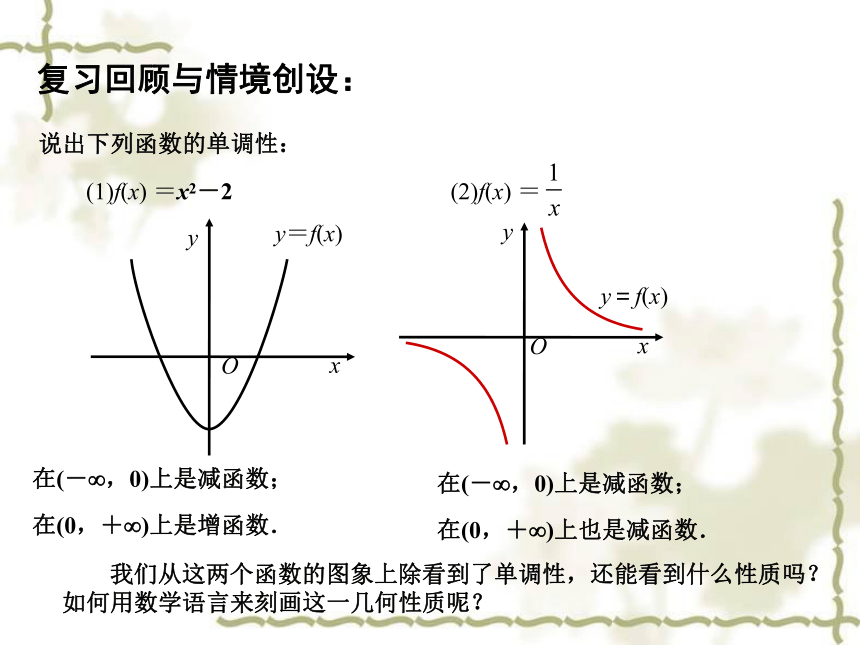
说出下列函数的单调性:
x
y
O
在(0,+ )上是增函数.
在(- ,0)上是减函数;
y=f(x)
我们从这两个函数的图象上除看到了单调性,还能看到什么性质吗?
如何用数学语言来刻画这一几何性质呢?
x
y
O
y=f(x)
(1)f(x) =x2-2
(2)f(x) =
在(0,+ )上也是减函数.
在(- ,0)上是减函数;
数学建构:
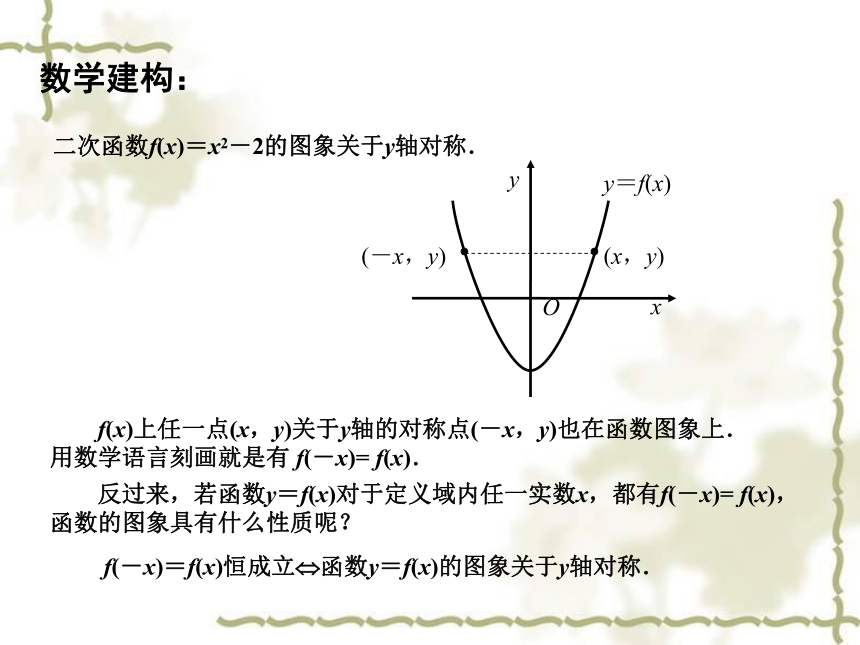
二次函数f(x)=x2-2的图象关于y轴对称.
x
y
O
f(x)上任一点(x,y)关于y轴的对称点(-x,y)也在函数图象上.
用数学语言刻画就是有 f(-x)= f(x).
(x,y)
(-x,y)
y=f(x)
反过来,若函数y=f(x)对于定义域内任一实数x,都有f(-x)= f(x),
函数的图象具有什么性质呢?
f(-x)=f(x)恒成立 函数y=f(x)的图象关于y轴对称.
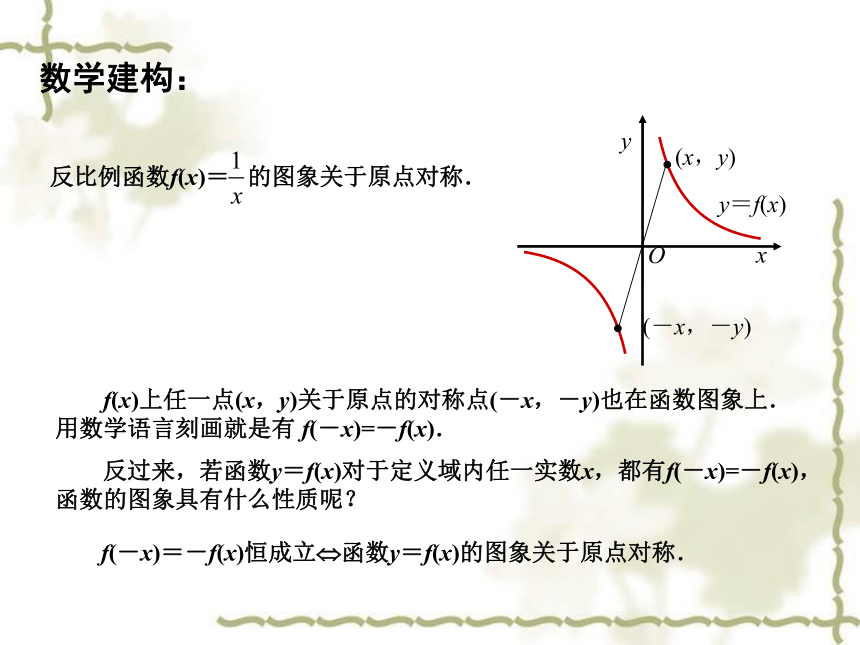
反比例函数f(x)= 的图象关于原点对称.
x
y
O
f(x)上任一点(x,y)关于原点的对称点(-x,-y)也在函数图象上.
用数学语言刻画就是有 f(-x)=-f(x).
(x,y)
(-x,-y)
y=f(x)
反过来,若函数y=f(x)对于定义域内任一实数x,都有f(-x)=-f(x),
函数的图象具有什么性质呢?
f(-x)=-f(x)恒成立 函数y=f(x)的图象关于原点对称.
数学建构:
已知函数f(x)的定义域为A,
若对任意的x A ,都有f(-x)= -f(x),则称函数f(x)为奇函数.
奇函数的图象关于原点对称.
偶函数的图象关于y轴对称.
如果对任意的x A ,都有f(-x)= f(x),则称函数f(x)为偶函数.
数学建构:
如果函数f(x)是奇函数或偶函数,我们就说函数f(x)具有奇偶性.
反之则说函数不具有奇偶性.
例1.判断函数f(x)=x3+5x的奇偶性.
数学应用:
对于定义在R上的函数f(x),下列判断是否正确:
(1)若f(2)=f(-2),则f(x)是偶函数
(2)若f(2)≠f(-2),则f(x)不是偶函数
(3)若f(2)=f(-2),则f(x)不是奇函数
对于f(x)=x2-2x-1 ,f(1)= -2 , f(-1)=2,
显然有f(-1)=-f(1),函数是奇函数吗?
数学应用:
例2.判定下列函数是否为偶函数或奇函数:
(1)f(x)=x3-x; (2)f(x)=2x;
(3)f(x)=2|x|; (4)f(x)=x-1
x [-1,3]
练习:判断下列函数的奇偶性:
1.f(x)=x+
2.f(x)=x2+
3.f(x)=
3.f(x)=
小结:判断函数具有奇偶性用定义,而判定函数不具有奇偶性
只需看定义域或举反例.
数学应用:
x
y
O
已知奇函数f(x)在y轴右边的图象如图所示,请你画出左边的图象.
如果f(x)是偶函数呢?
数学应用:
x
y
O
设奇函数f(x)的定义域为[-5,5],当x [0,5]时, f(x)的图象如图所示,试写出不等式f(x)<0的解集.
如果f(x)是偶函数呢?
5
2
数学应用:
x
y
O
x0
x
y
O
2
2
上面两个图象也具有对称性,所对应的函数具有奇偶性吗?
x
y
O
下面两幅呢?
x
y
O
数学应用:
二次函数y=ax2+bx+c(a≠0)是偶函数的条件是 .
一次函数y=kx+b(k≠0)是奇函数的条件是 .
b=0
b=0
函数y=f(x)的奇偶性,是函数的本质属性,可看作是将对称性特殊化.
奇函数是中心对称的特殊形式,
偶函数则是轴对称的特殊形式.
数学应用:
例3.判断函数f(x)=
x2+2x,x≤0,
x2-2x,x>0
的奇偶性.
变式:判断函数f(x)=
x2-x-1,x<0
x2+x-1,x>0
的奇偶性.
小结:分段函数奇偶性的判断:
先画出图象,结合图象给出奇偶性的结论,再利用定义分段证明.
注:若数字0在定义域内,不能忽略讨论,
且对于奇函数f(x),若0在定义域内,则必有结论f(0)=
0
数学应用:
例4.已知函数f(x)=x5+2ax3+3bx -2,若f(-2)=3,求f(2)的值.
小结:1.利用规律f(-x)+f(x)等于常数项的2倍解题.
2.一个定义域关于数0对称的函数,总可以表示成一个奇函数与
一个偶函数的和.
变式:若函数f(x)是R上的奇函数,g(x)是R上的偶函数,且f(x)+ g(x)=
1
x2-x+1
,求f(x)与 g(x)的解析式.
数学应用:
1.定义域内.
2.任意一个x.
3.都有
f(-x)=f(x)
f(-x)= -f(x)
偶函数
奇函数
有理函数
不含有奇次幂项
不含有偶次幂项
4.判定具有奇偶性
判定不具有奇偶性
用定义
看定义域
举反例
小结:
作业:
思考下列函数的奇偶性:
P43第5,6题.
(3)f(x)=(x-1)·
(4)f(x)=(x-1)·
(1)f(x)=|x+1|+ |x-1|
(2)f(x)=|x+1|- |x-1|
(5)f(x)=
高中数学 必修1
复习回顾与情境创设:
说出下列函数的单调性:
x
y
O
在(0,+ )上是增函数.
在(- ,0)上是减函数;
y=f(x)
我们从这两个函数的图象上除看到了单调性,还能看到什么性质吗?
如何用数学语言来刻画这一几何性质呢?
x
y
O
y=f(x)
(1)f(x) =x2-2
(2)f(x) =
在(0,+ )上也是减函数.
在(- ,0)上是减函数;
数学建构:
二次函数f(x)=x2-2的图象关于y轴对称.
x
y
O
f(x)上任一点(x,y)关于y轴的对称点(-x,y)也在函数图象上.
用数学语言刻画就是有 f(-x)= f(x).
(x,y)
(-x,y)
y=f(x)
反过来,若函数y=f(x)对于定义域内任一实数x,都有f(-x)= f(x),
函数的图象具有什么性质呢?
f(-x)=f(x)恒成立 函数y=f(x)的图象关于y轴对称.
反比例函数f(x)= 的图象关于原点对称.
x
y
O
f(x)上任一点(x,y)关于原点的对称点(-x,-y)也在函数图象上.
用数学语言刻画就是有 f(-x)=-f(x).
(x,y)
(-x,-y)
y=f(x)
反过来,若函数y=f(x)对于定义域内任一实数x,都有f(-x)=-f(x),
函数的图象具有什么性质呢?
f(-x)=-f(x)恒成立 函数y=f(x)的图象关于原点对称.
数学建构:
已知函数f(x)的定义域为A,
若对任意的x A ,都有f(-x)= -f(x),则称函数f(x)为奇函数.
奇函数的图象关于原点对称.
偶函数的图象关于y轴对称.
如果对任意的x A ,都有f(-x)= f(x),则称函数f(x)为偶函数.
数学建构:
如果函数f(x)是奇函数或偶函数,我们就说函数f(x)具有奇偶性.
反之则说函数不具有奇偶性.
例1.判断函数f(x)=x3+5x的奇偶性.
数学应用:
对于定义在R上的函数f(x),下列判断是否正确:
(1)若f(2)=f(-2),则f(x)是偶函数
(2)若f(2)≠f(-2),则f(x)不是偶函数
(3)若f(2)=f(-2),则f(x)不是奇函数
对于f(x)=x2-2x-1 ,f(1)= -2 , f(-1)=2,
显然有f(-1)=-f(1),函数是奇函数吗?
数学应用:
例2.判定下列函数是否为偶函数或奇函数:
(1)f(x)=x3-x; (2)f(x)=2x;
(3)f(x)=2|x|; (4)f(x)=x-1
x [-1,3]
练习:判断下列函数的奇偶性:
1.f(x)=x+
2.f(x)=x2+
3.f(x)=
3.f(x)=
小结:判断函数具有奇偶性用定义,而判定函数不具有奇偶性
只需看定义域或举反例.
数学应用:
x
y
O
已知奇函数f(x)在y轴右边的图象如图所示,请你画出左边的图象.
如果f(x)是偶函数呢?
数学应用:
x
y
O
设奇函数f(x)的定义域为[-5,5],当x [0,5]时, f(x)的图象如图所示,试写出不等式f(x)<0的解集.
如果f(x)是偶函数呢?
5
2
数学应用:
x
y
O
x0
x
y
O
2
2
上面两个图象也具有对称性,所对应的函数具有奇偶性吗?
x
y
O
下面两幅呢?
x
y
O
数学应用:
二次函数y=ax2+bx+c(a≠0)是偶函数的条件是 .
一次函数y=kx+b(k≠0)是奇函数的条件是 .
b=0
b=0
函数y=f(x)的奇偶性,是函数的本质属性,可看作是将对称性特殊化.
奇函数是中心对称的特殊形式,
偶函数则是轴对称的特殊形式.
数学应用:
例3.判断函数f(x)=
x2+2x,x≤0,
x2-2x,x>0
的奇偶性.
变式:判断函数f(x)=
x2-x-1,x<0
x2+x-1,x>0
的奇偶性.
小结:分段函数奇偶性的判断:
先画出图象,结合图象给出奇偶性的结论,再利用定义分段证明.
注:若数字0在定义域内,不能忽略讨论,
且对于奇函数f(x),若0在定义域内,则必有结论f(0)=
0
数学应用:
例4.已知函数f(x)=x5+2ax3+3bx -2,若f(-2)=3,求f(2)的值.
小结:1.利用规律f(-x)+f(x)等于常数项的2倍解题.
2.一个定义域关于数0对称的函数,总可以表示成一个奇函数与
一个偶函数的和.
变式:若函数f(x)是R上的奇函数,g(x)是R上的偶函数,且f(x)+ g(x)=
1
x2-x+1
,求f(x)与 g(x)的解析式.
数学应用:
1.定义域内.
2.任意一个x.
3.都有
f(-x)=f(x)
f(-x)= -f(x)
偶函数
奇函数
有理函数
不含有奇次幂项
不含有偶次幂项
4.判定具有奇偶性
判定不具有奇偶性
用定义
看定义域
举反例
小结:
作业:
思考下列函数的奇偶性:
P43第5,6题.
(3)f(x)=(x-1)·
(4)f(x)=(x-1)·
(1)f(x)=|x+1|+ |x-1|
(2)f(x)=|x+1|- |x-1|
(5)f(x)=
