苏教版高中数学必修1课件 2.1.3 函数的简单性质(4)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.1.3 函数的简单性质(4) |

|
|
| 格式 | rar | ||
| 文件大小 | 106.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
高中数学 必修1
奇函数、偶函数的定义:
都有f(-x)= -f(x),则称函数f(x)为奇函数.
奇函数的图象关于原点对称.
偶函数的图象关于y轴对称.
都有f(-x)= f(x),则称函数f(x)为偶函数.
情境问题:
如果函数f(x)是奇函数或偶函数,我们就说函数f(x)具有奇偶性.
反之则说函数不具有奇偶性.
奇偶性和单调性都是函数的本质属性,这二者之间有何联系呢?
已知函数f(x)的定义域为A,若对任意的x A ,
数学探究:
画出函数f(x)=x2-2|x|-1图象,通过图象,指出它的单调区间,并判定它的奇偶性.
数学应用:
例1.已知奇函数f(x)在区间[a,b](0<a<b)上是单调减函数,
求证:函数f(x)在区间[-b,-a]上仍是单调减函数.
若f(x)是偶函数,则单调性恰好相反.
若f(x)是奇函数,则在两个区间上的单调性一致;
若(a,b)是奇函数f(x)的单调区间,则(-b,-a)也是单调区间,
数学应用:
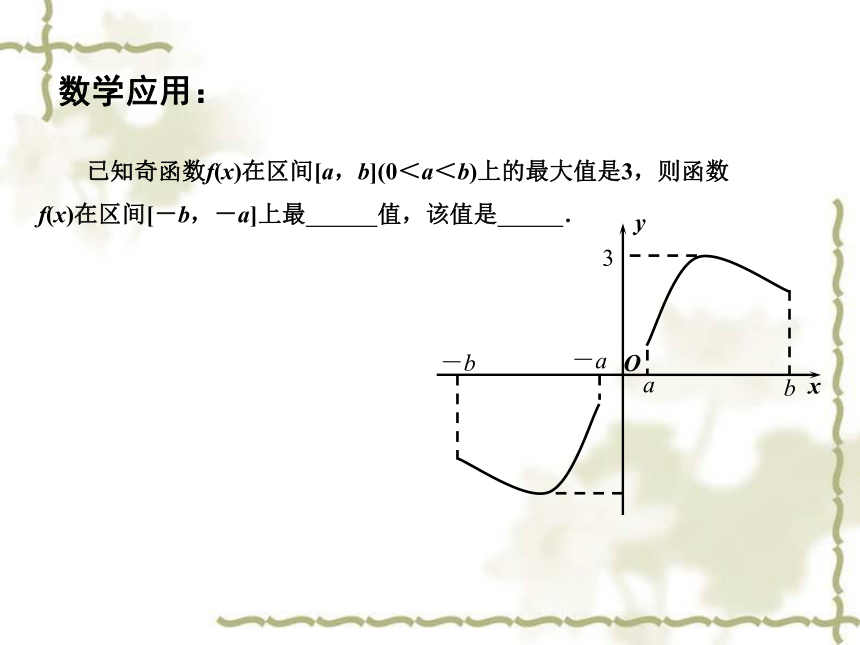
已知奇函数f(x)在区间[a,b](0<a<b)上的最大值是3,则函数f(x)在区间[-b,-a]上最 值,该值是 .
x
y
O
a
b
-b
-a
3
设函数f(x)是R上的偶函数,且在(- ,0)上是增函数.则f(-2)与f(a2-2a+3)(a R)的大小关系是 .
f(-2)≥f(a2-2a+3)
函数f(x)是定义在(-1,1)上的奇函数,且在定义域上是增函数.
若f(1-a)+f(1-a2)>0,则实数a的取值范围是 .
0<a<1
数学应用:
已知函数f(x+1)是偶函数,则函数f(x)的对称轴是 .
x=1
数学应用:
变式:已知函数f(x+1)是奇函数,则函数f(x)的对称中是 .
(1,0)
若函数f(x)=x2-ax-b满足对于任意的实数x都有f(1+x)=f(1-x),且f(x)的最小值为-2,求实数a,b的值.
已知定义域为R的函数f(x)在(8,+ )上为减函数,且函数y=f(x+8)函数为偶函数,则f(2),f(8),f(10)的大小关系为 .
已知函数f (x)是定义在R上的偶函数,且f (x)=f(2-x),若f (x)在区间[1,2]上是减函数,则f (x)在区间 [-2,-1]上的单调性为 ,在区间[3,4]上的单调性为 .
单调增
数学应用:
f(8)<f(10)< f(2)
单调减
x
y
O
例2.已知函数y=f(x)是R上的奇函数,而且x>0时,f(x) =x-1,试求函数y=f(x)的表达式.
数学应用:
练习 函数f (x)=x| x |+px,p为常数,则 ( )
A.对于任何常数p,f (x)既不是奇函数也不是偶函数
B.对于任何常数p,f (x)是奇函数
C.对于任何常数p,f (x)是偶函数
D.只有当p=0时,f (x)是奇函数
B
数学应用:
例3.已知函数f(x)对于任意的实数x、y,都有f(x+y)=f(x)+f(y)
(1)求f(0)的值;
(2)试判断函数f(x)的奇偶性;
(3)若x>0都有f(x)>0,试判断函数的单调性.
数学应用:
抽象函数是以常见的函数作为模型.
赋值是寻找解决抽象函数的突破口.
抽象函数常以单调性和奇偶性为考查内容.
数学建构:
函数性质的运用
用奇偶性确定单调性;
用奇偶性确定解析式;
抽象函数问题.
如果函数具有奇偶性,那么该函数的定义域关于数零对称.
小结:
作业:
课本43页6,8,9,10.
高中数学 必修1
奇函数、偶函数的定义:
都有f(-x)= -f(x),则称函数f(x)为奇函数.
奇函数的图象关于原点对称.
偶函数的图象关于y轴对称.
都有f(-x)= f(x),则称函数f(x)为偶函数.
情境问题:
如果函数f(x)是奇函数或偶函数,我们就说函数f(x)具有奇偶性.
反之则说函数不具有奇偶性.
奇偶性和单调性都是函数的本质属性,这二者之间有何联系呢?
已知函数f(x)的定义域为A,若对任意的x A ,
数学探究:
画出函数f(x)=x2-2|x|-1图象,通过图象,指出它的单调区间,并判定它的奇偶性.
数学应用:
例1.已知奇函数f(x)在区间[a,b](0<a<b)上是单调减函数,
求证:函数f(x)在区间[-b,-a]上仍是单调减函数.
若f(x)是偶函数,则单调性恰好相反.
若f(x)是奇函数,则在两个区间上的单调性一致;
若(a,b)是奇函数f(x)的单调区间,则(-b,-a)也是单调区间,
数学应用:
已知奇函数f(x)在区间[a,b](0<a<b)上的最大值是3,则函数f(x)在区间[-b,-a]上最 值,该值是 .
x
y
O
a
b
-b
-a
3
设函数f(x)是R上的偶函数,且在(- ,0)上是增函数.则f(-2)与f(a2-2a+3)(a R)的大小关系是 .
f(-2)≥f(a2-2a+3)
函数f(x)是定义在(-1,1)上的奇函数,且在定义域上是增函数.
若f(1-a)+f(1-a2)>0,则实数a的取值范围是 .
0<a<1
数学应用:
已知函数f(x+1)是偶函数,则函数f(x)的对称轴是 .
x=1
数学应用:
变式:已知函数f(x+1)是奇函数,则函数f(x)的对称中是 .
(1,0)
若函数f(x)=x2-ax-b满足对于任意的实数x都有f(1+x)=f(1-x),且f(x)的最小值为-2,求实数a,b的值.
已知定义域为R的函数f(x)在(8,+ )上为减函数,且函数y=f(x+8)函数为偶函数,则f(2),f(8),f(10)的大小关系为 .
已知函数f (x)是定义在R上的偶函数,且f (x)=f(2-x),若f (x)在区间[1,2]上是减函数,则f (x)在区间 [-2,-1]上的单调性为 ,在区间[3,4]上的单调性为 .
单调增
数学应用:
f(8)<f(10)< f(2)
单调减
x
y
O
例2.已知函数y=f(x)是R上的奇函数,而且x>0时,f(x) =x-1,试求函数y=f(x)的表达式.
数学应用:
练习 函数f (x)=x| x |+px,p为常数,则 ( )
A.对于任何常数p,f (x)既不是奇函数也不是偶函数
B.对于任何常数p,f (x)是奇函数
C.对于任何常数p,f (x)是偶函数
D.只有当p=0时,f (x)是奇函数
B
数学应用:
例3.已知函数f(x)对于任意的实数x、y,都有f(x+y)=f(x)+f(y)
(1)求f(0)的值;
(2)试判断函数f(x)的奇偶性;
(3)若x>0都有f(x)>0,试判断函数的单调性.
数学应用:
抽象函数是以常见的函数作为模型.
赋值是寻找解决抽象函数的突破口.
抽象函数常以单调性和奇偶性为考查内容.
数学建构:
函数性质的运用
用奇偶性确定单调性;
用奇偶性确定解析式;
抽象函数问题.
如果函数具有奇偶性,那么该函数的定义域关于数零对称.
小结:
作业:
课本43页6,8,9,10.
