苏教版高中数学必修1课件 2.2.2 指数函数(1)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.2.2 指数函数(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 120.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
高中数学 必修1
情境问题:
某种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个……一个细胞分裂x次后,得到细胞的个数为y,则y与x的函数关系是什么呢?
从我国辽东半岛普兰店附近的泥炭中发掘出的古莲子至今大部分还能发芽开花.这些古莲子是多少年以前的遗物呢?要测定古生物的年代,可以用放射性碳法:在动植物体内都含有微量的放射性14C.动植物死亡后,停止了新陈代谢,14C不再产生,且原有的14C会自动衰减,大约每经过5730年(14C的半衰期),它的残余量只有原始量的一半.经过科学测定,若14C的原始含量为1,经过x年后的残留量为y,则 y与x的函数关系是什么呢?
y =2x
y =ax,这里的a为常数,0< a <1 .
………………………………(1)
…………(2)
(1)和(2)有什么相同的特征?
数学建构:
2.指数函数的定义域是什么?
3.函数y=2x和函数y=x2有什么区别?
4.函数y=2·3x和y=23x是不是指数函数?
一般地,函数y=ax(a>0且a≠1)叫做指数函数.
指数函数的定义:
1.在指数函数的解析式y=ax中,为什么要规定a>0且a≠1?
思考问题:
数学应用:
(1)y=2·3x;(2)y=3x-1;(3)y=x3; (4)y=-3x;
(5)y=(-3)x;(6)y= x;(7)y=3x2;(8)y=xx;
(9)y =4-x,(10)y=(2a-1)x(a> ,且a≠1).
练习:判断下列函数是否是指数函数:
数学建构:
指数函数的图象与性质:
在同一坐标系画出(1)y=2x,(2)y= 的图象,
观察并总结函数y=ax(a>0,且a≠1)的性质.
借助于计算机在同一坐标系内画出函数(1)y=10x,(2)y=2.5x,(3)y=0.1x,(2)y=0.4x的图象,进一步验证函数y=ax(a>0,且a≠1)的性质,
并探讨函数y=ax与y=a-x(a>0,且a≠1)二者之间的关系.
数学建构:
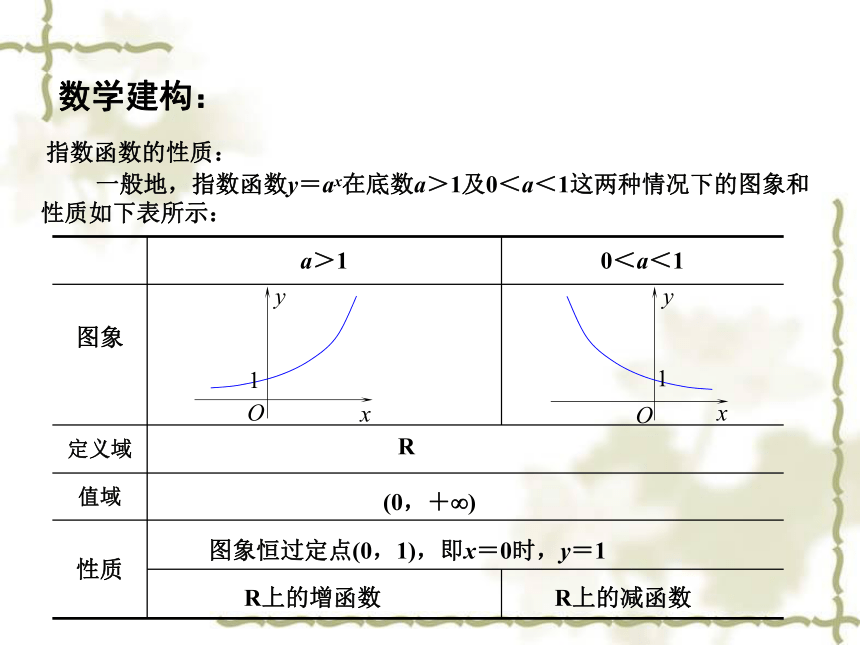
一般地,指数函数y=ax在底数a>1及0<a<1这两种情况下的图象和性质如下表所示:
a>1 0<a<1
图象
定义域
值域
性质
R
(0,+ )
x
y
O
1
R上的减函数
x
y
O
1
图象恒过定点(0,1),即x=0时,y=1
指数函数的性质:
R上的增函数
数学应用:
(1)1.52.5,1.53.2;
(2)0.51.2,0.51.5;
(3)1.50.3,0.81.2.
小结:
在解决比较两个数的大小问题时,一般情况下是将其看作一个函数的两个函数值,利用函数的单调性直接比较它们的大小,如(1)、(2).当两个数不能直接比较时,我们可以将其与一个已知的过渡数进行比较大小,从而得出该两数的大小关系.常用来过渡的值有0或±1等,根据实际问题也可能是其它数值.
例1.比较大小
数学应用:
义域时,必须注意以前我们求函数定义域时的一些限制条件:
虽然指数函数y=ax的定义域R,但是在求与指数函数有关的复合函数的定
例2.求下列函数的定义域,并探求其值域.
(1) y=
(2) y=
说明:
(1)分式的分母不能为0;
(2)偶次根式的被开方数大于或等于0;
(3)0的0次幂没有意义;
(4)在实际问题中必须使实际问题有意义.
数学应用:
解 由f(x)>g(x),得
例3.函数f(x)=a ,g(x)=a (a>0且a≠1) ,若f(x)>g(x),
x2-3x+1
x2+2x-4
求x的取值范围.
a >a
x2-3x+1
x2+2x-4
(1)当a>1时,x2-3x+1 >x2+2x-4,解得x<1
(2)当0<a<1时,x2-3x+1<x2+2x-4,解得x>1
若a>1,则x的取值范围为{x|x<1};
综上所述:
若0<a<1,则x的取值范围为{x|x>1}.
数学应用:
若函数y=(a2-3a+3)·ax是指数函数,则它的单调性为 .
小结:
指数函数的定义:
函数y=ax(a>0,a≠1)叫做指数函数.
指数函数的图象和性质:
指数函数的定义域为R,图象恒过点(0,1),
当0<a<1时,指数函数在R上递减;
当a>1时,指数函数在R上递增.
利用指数函数的性质进行大小比较.
作业:
P54习题2.2(2)2,3,4.
课后探究:
已知函数f (x)=
.
给出f (x)的定义域,值域,奇偶性和单调性.
高中数学 必修1
情境问题:
某种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个……一个细胞分裂x次后,得到细胞的个数为y,则y与x的函数关系是什么呢?
从我国辽东半岛普兰店附近的泥炭中发掘出的古莲子至今大部分还能发芽开花.这些古莲子是多少年以前的遗物呢?要测定古生物的年代,可以用放射性碳法:在动植物体内都含有微量的放射性14C.动植物死亡后,停止了新陈代谢,14C不再产生,且原有的14C会自动衰减,大约每经过5730年(14C的半衰期),它的残余量只有原始量的一半.经过科学测定,若14C的原始含量为1,经过x年后的残留量为y,则 y与x的函数关系是什么呢?
y =2x
y =ax,这里的a为常数,0< a <1 .
………………………………(1)
…………(2)
(1)和(2)有什么相同的特征?
数学建构:
2.指数函数的定义域是什么?
3.函数y=2x和函数y=x2有什么区别?
4.函数y=2·3x和y=23x是不是指数函数?
一般地,函数y=ax(a>0且a≠1)叫做指数函数.
指数函数的定义:
1.在指数函数的解析式y=ax中,为什么要规定a>0且a≠1?
思考问题:
数学应用:
(1)y=2·3x;(2)y=3x-1;(3)y=x3; (4)y=-3x;
(5)y=(-3)x;(6)y= x;(7)y=3x2;(8)y=xx;
(9)y =4-x,(10)y=(2a-1)x(a> ,且a≠1).
练习:判断下列函数是否是指数函数:
数学建构:
指数函数的图象与性质:
在同一坐标系画出(1)y=2x,(2)y= 的图象,
观察并总结函数y=ax(a>0,且a≠1)的性质.
借助于计算机在同一坐标系内画出函数(1)y=10x,(2)y=2.5x,(3)y=0.1x,(2)y=0.4x的图象,进一步验证函数y=ax(a>0,且a≠1)的性质,
并探讨函数y=ax与y=a-x(a>0,且a≠1)二者之间的关系.
数学建构:
一般地,指数函数y=ax在底数a>1及0<a<1这两种情况下的图象和性质如下表所示:
a>1 0<a<1
图象
定义域
值域
性质
R
(0,+ )
x
y
O
1
R上的减函数
x
y
O
1
图象恒过定点(0,1),即x=0时,y=1
指数函数的性质:
R上的增函数
数学应用:
(1)1.52.5,1.53.2;
(2)0.51.2,0.51.5;
(3)1.50.3,0.81.2.
小结:
在解决比较两个数的大小问题时,一般情况下是将其看作一个函数的两个函数值,利用函数的单调性直接比较它们的大小,如(1)、(2).当两个数不能直接比较时,我们可以将其与一个已知的过渡数进行比较大小,从而得出该两数的大小关系.常用来过渡的值有0或±1等,根据实际问题也可能是其它数值.
例1.比较大小
数学应用:
义域时,必须注意以前我们求函数定义域时的一些限制条件:
虽然指数函数y=ax的定义域R,但是在求与指数函数有关的复合函数的定
例2.求下列函数的定义域,并探求其值域.
(1) y=
(2) y=
说明:
(1)分式的分母不能为0;
(2)偶次根式的被开方数大于或等于0;
(3)0的0次幂没有意义;
(4)在实际问题中必须使实际问题有意义.
数学应用:
解 由f(x)>g(x),得
例3.函数f(x)=a ,g(x)=a (a>0且a≠1) ,若f(x)>g(x),
x2-3x+1
x2+2x-4
求x的取值范围.
a >a
x2-3x+1
x2+2x-4
(1)当a>1时,x2-3x+1 >x2+2x-4,解得x<1
(2)当0<a<1时,x2-3x+1<x2+2x-4,解得x>1
若a>1,则x的取值范围为{x|x<1};
综上所述:
若0<a<1,则x的取值范围为{x|x>1}.
数学应用:
若函数y=(a2-3a+3)·ax是指数函数,则它的单调性为 .
小结:
指数函数的定义:
函数y=ax(a>0,a≠1)叫做指数函数.
指数函数的图象和性质:
指数函数的定义域为R,图象恒过点(0,1),
当0<a<1时,指数函数在R上递减;
当a>1时,指数函数在R上递增.
利用指数函数的性质进行大小比较.
作业:
P54习题2.2(2)2,3,4.
课后探究:
已知函数f (x)=
.
给出f (x)的定义域,值域,奇偶性和单调性.
