苏教版高中数学必修1课件 2.3.1 对数(1)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.3.1 对数(1) |  | |
| 格式 | rar | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 09:18:53 | ||
图片预览





文档简介
(共12张PPT)
高中数学 必修1
情境问题:
设x年可实现翻一番的目标,则有
假设2005年我国的国民生产总值为a亿元,如每年平均增长8%,那么经过多少年,国民生产总值可翻一番?
a(1+0.08)x=2a,即1.08x=2.
在指数式中,已知底数和指数,通过乘方运算可求幂;而已知指数和幂,则可通过用开方运算或分数指数幂运算求底数;已知底数和幂,如何求指数呢?
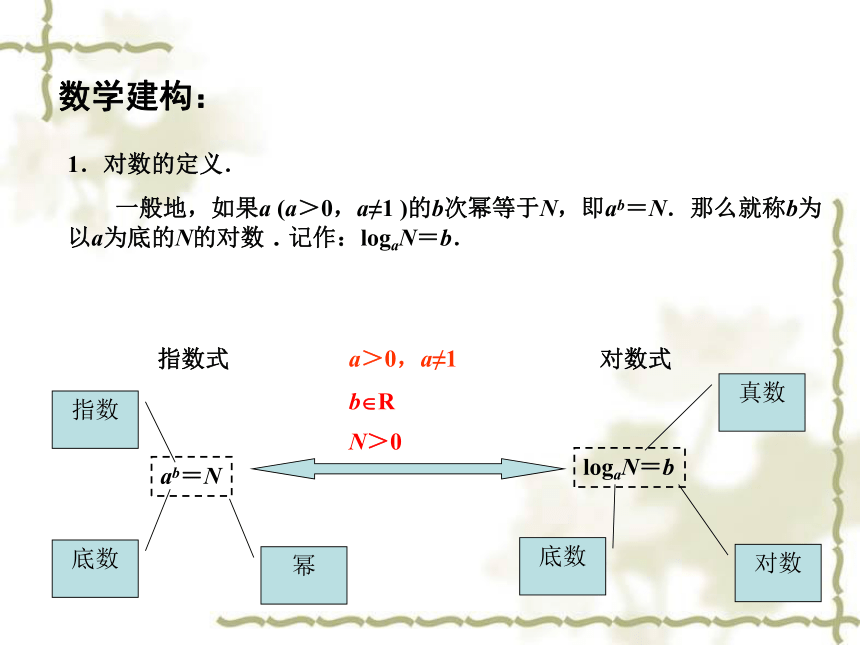
数学建构:
一般地,如果a (a>0,a≠1 )的b次幂等于N,即ab=N.那么就称b为以a为底的N的对数.记作:logaN=b.
1.对数的定义.
a>0,a≠1
b R
N>0
ab=N
对数式
指数式
logaN=b
底数
指数
幂
底数
真数
对数
数学应用:
例1.将下列各指数式改写成对数式.
(1)24=16
(2)3-3=
(3)5a=20
(4) =0.45
log216=4
log3
=-3
logaab=b
log520=a
log
0.45=b
a
=N
logaN
对数恒等式
对数是一种运算
对数是一个结果
对数的本质
数学应用:
例2.求下列各式的值:
(1)log264
(2)log927
根据对数的定义,写出下列各式的值(其中a>0,a≠1 )
(1)log10100
(2)log255
(3)log2
(4)log
(5)log33
(6)logaa
(7)log31
(8)loga1
3
2
-1
-1
1
1
0
0
数学建构:
2.关于对数的几个要点.
(1)负数和0没有对数;
(2)常用对数:底数为10的对数称为常用对数,记为lgN;
(3) 自然对数:底数为e的对数称为常用对数,记为lnN.
① loga ab=b;
② a =N
logaN
(4)对数恒等式
数学应用:
例3.将下列对数式改写成指数式.
(1) log5125=3
(3) lga=-1.699
(2)
数学应用:
例4.已知loga2=m,loga3=n,求a2m+n的值.
求22+ 的值.
log25
数学应用:
练习
0
0
0
-13
1.(1)lg(lg10)= ;
(2)lg(lne)= ;
(3)log6[log4(log381)]= ;
(4)log3( )=1,则x=________.
数学应用:
练习
2.把logx =z表示成指数式是 .
3.设
,则满足
的x值为_______.
.
5.设x=log23,求
小结:
ab=N logaN=b.
注: (1)负数和0没有对数;
(2)常用对数与自然对数;
(3)对数恒等式.
① loga ab=b;
②
作业:
P63习题2.3(1)1,2,3(1)~(4).
高中数学 必修1
情境问题:
设x年可实现翻一番的目标,则有
假设2005年我国的国民生产总值为a亿元,如每年平均增长8%,那么经过多少年,国民生产总值可翻一番?
a(1+0.08)x=2a,即1.08x=2.
在指数式中,已知底数和指数,通过乘方运算可求幂;而已知指数和幂,则可通过用开方运算或分数指数幂运算求底数;已知底数和幂,如何求指数呢?
数学建构:
一般地,如果a (a>0,a≠1 )的b次幂等于N,即ab=N.那么就称b为以a为底的N的对数.记作:logaN=b.
1.对数的定义.
a>0,a≠1
b R
N>0
ab=N
对数式
指数式
logaN=b
底数
指数
幂
底数
真数
对数
数学应用:
例1.将下列各指数式改写成对数式.
(1)24=16
(2)3-3=
(3)5a=20
(4) =0.45
log216=4
log3
=-3
logaab=b
log520=a
log
0.45=b
a
=N
logaN
对数恒等式
对数是一种运算
对数是一个结果
对数的本质
数学应用:
例2.求下列各式的值:
(1)log264
(2)log927
根据对数的定义,写出下列各式的值(其中a>0,a≠1 )
(1)log10100
(2)log255
(3)log2
(4)log
(5)log33
(6)logaa
(7)log31
(8)loga1
3
2
-1
-1
1
1
0
0
数学建构:
2.关于对数的几个要点.
(1)负数和0没有对数;
(2)常用对数:底数为10的对数称为常用对数,记为lgN;
(3) 自然对数:底数为e的对数称为常用对数,记为lnN.
① loga ab=b;
② a =N
logaN
(4)对数恒等式
数学应用:
例3.将下列对数式改写成指数式.
(1) log5125=3
(3) lga=-1.699
(2)
数学应用:
例4.已知loga2=m,loga3=n,求a2m+n的值.
求22+ 的值.
log25
数学应用:
练习
0
0
0
-13
1.(1)lg(lg10)= ;
(2)lg(lne)= ;
(3)log6[log4(log381)]= ;
(4)log3( )=1,则x=________.
数学应用:
练习
2.把logx =z表示成指数式是 .
3.设
,则满足
的x值为_______.
.
5.设x=log23,求
小结:
ab=N logaN=b.
注: (1)负数和0没有对数;
(2)常用对数与自然对数;
(3)对数恒等式.
① loga ab=b;
②
作业:
P63习题2.3(1)1,2,3(1)~(4).
