苏教版高中数学必修1课件 2.3.1 对数(3)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.3.1 对数(3) |  | |
| 格式 | rar | ||
| 文件大小 | 122.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 09:18:53 | ||
图片预览




文档简介
(共10张PPT)
高中数学 必修1
情境问题:
一般地,对于a>0,a≠1 ,M>0,N>0,都有
对数的性质:
(1)已知lg2=0.3010,lg3=0.4771,lg12的值约为多少?
(2)能否利用lg2与lg3的值,近似求log23的值呢,这三者之间有什么呢?
loga(M·N)= logaM+logaN
loga =logaM-logaN
logaMn=nlogaM, n R
数学建构:
对数的换底公式:
logaN=
其中a>0,a≠1, c>0,c≠1, N >0
logcN
logca
换底公式的运用:
logab·logba=1;
logab=
数学应用:
例1 求log89×log332的值.
变式:
(1)求log89×log2732的值;
(2)若log34×log25×log5m=2,则m= .
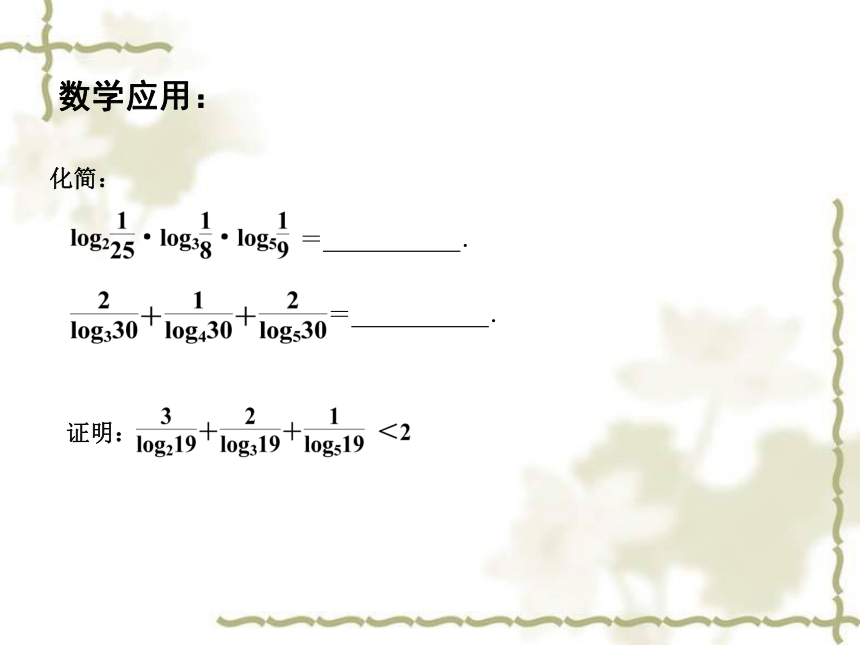
数学应用:
化简:
= .
= .
证明:
数学应用:
例2 设xa=yb=zc,且 .求证:z=xy.
变式:
设正实数a、b、c 满足3a=4b=6c,
(2)比较3a、4b、6c的大小.
(1)求证: ;
数学应用:
例3.如图,2000年我国国内生产总值(GDP)为89442亿元, 如果我国的GDP年均增长7.8%左右,按照这个增长速度,在2000年的基础上,经过多少年后,我国GDP才能实现比2000年翻两番的目标?(lg2≈0.3010,lg1.078≈0.0326,结果保留整数).
数学应用:
例4.在本章第2.2.2节的开头问题中,已知测得出土的古莲子中的残余量占原来的87.9%,试推算古莲子的生活年代(lg2≈0.3010,lg0.879≈-0.0560,结果保留整数).
小结:
换底公式中一个重要的恒等式: logaN logN a=1
1.对数的换底公式:
logaN=
logcN
logca
2.换底公式的应用及应用的条件.
作业:
P63习题2.3(1)6,7,8.
高中数学 必修1
情境问题:
一般地,对于a>0,a≠1 ,M>0,N>0,都有
对数的性质:
(1)已知lg2=0.3010,lg3=0.4771,lg12的值约为多少?
(2)能否利用lg2与lg3的值,近似求log23的值呢,这三者之间有什么呢?
loga(M·N)= logaM+logaN
loga =logaM-logaN
logaMn=nlogaM, n R
数学建构:
对数的换底公式:
logaN=
其中a>0,a≠1, c>0,c≠1, N >0
logcN
logca
换底公式的运用:
logab·logba=1;
logab=
数学应用:
例1 求log89×log332的值.
变式:
(1)求log89×log2732的值;
(2)若log34×log25×log5m=2,则m= .
数学应用:
化简:
= .
= .
证明:
数学应用:
例2 设xa=yb=zc,且 .求证:z=xy.
变式:
设正实数a、b、c 满足3a=4b=6c,
(2)比较3a、4b、6c的大小.
(1)求证: ;
数学应用:
例3.如图,2000年我国国内生产总值(GDP)为89442亿元, 如果我国的GDP年均增长7.8%左右,按照这个增长速度,在2000年的基础上,经过多少年后,我国GDP才能实现比2000年翻两番的目标?(lg2≈0.3010,lg1.078≈0.0326,结果保留整数).
数学应用:
例4.在本章第2.2.2节的开头问题中,已知测得出土的古莲子中的残余量占原来的87.9%,试推算古莲子的生活年代(lg2≈0.3010,lg0.879≈-0.0560,结果保留整数).
小结:
换底公式中一个重要的恒等式: logaN logN a=1
1.对数的换底公式:
logaN=
logcN
logca
2.换底公式的应用及应用的条件.
作业:
P63习题2.3(1)6,7,8.
