苏教版高中数学必修1课件 2.3.2 对数函数(2)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.3.2 对数函数(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 123.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
高中数学 必修1
情境问题:
对数函数的定义:
函数y=logax (a>0,a≠1)叫做对数函数.
对数函数的定义域为(0,+ ),值域为R .
对数函数的图象和性质:
对数函数的图象恒过点(1,0),
当0<a<1时,对数函数在(0,+ ) 上递减;
当a>1时,对数函数在(0,+ )上递增.
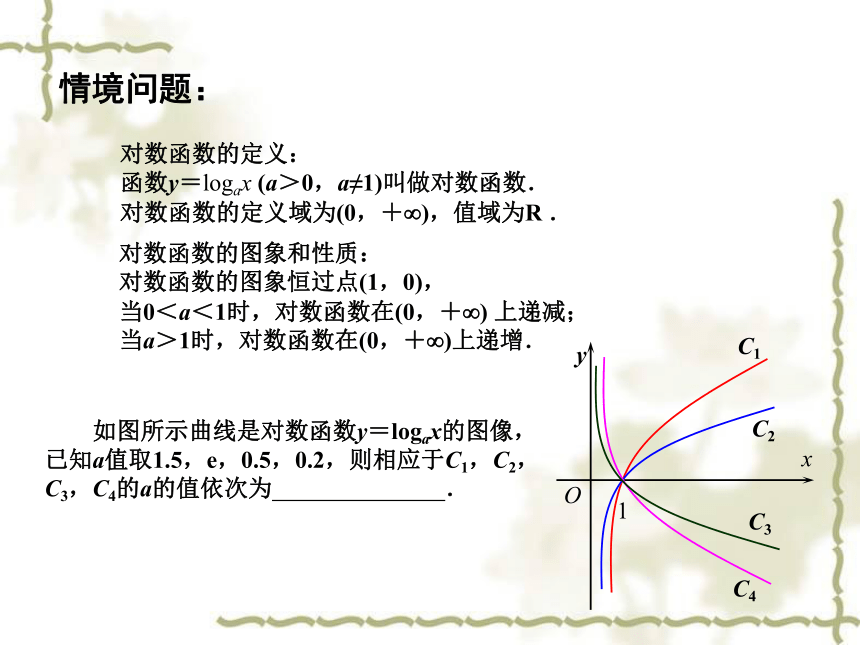
如图所示曲线是对数函数y=logax的图像,
已知a值取1.5,e,0.5,0.2,则相应于C1,C2,
C3,C4的a的值依次为 .
1
O
y
x
C1
C2
C3
C4
数学应用:
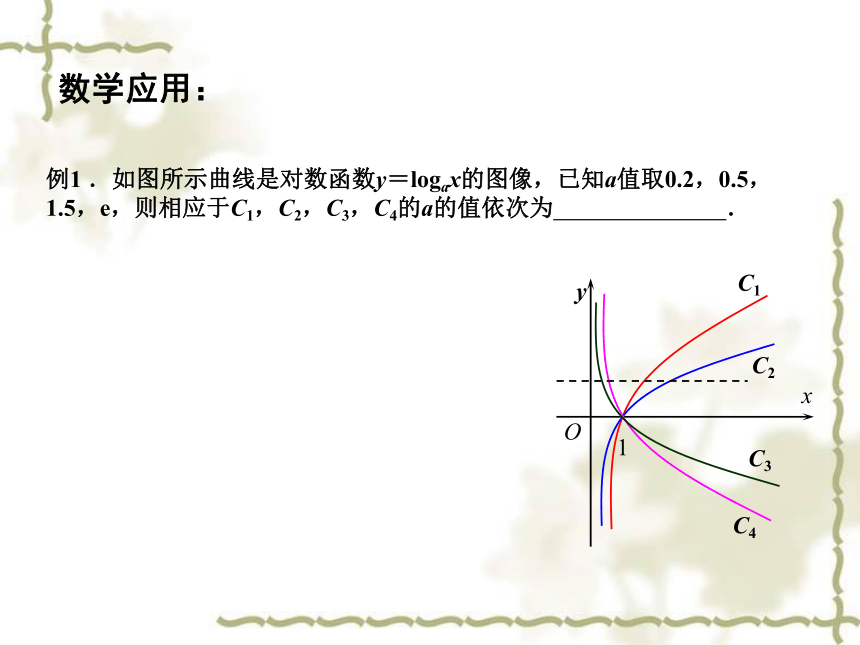
例1 .如图所示曲线是对数函数y=logax的图像,已知a值取0.2,0.5, 1.5,e,则相应于C1,C2,C3,C4的a的值依次为 .
1
O
y
x
C1
C2
C3
C4
数学探究:
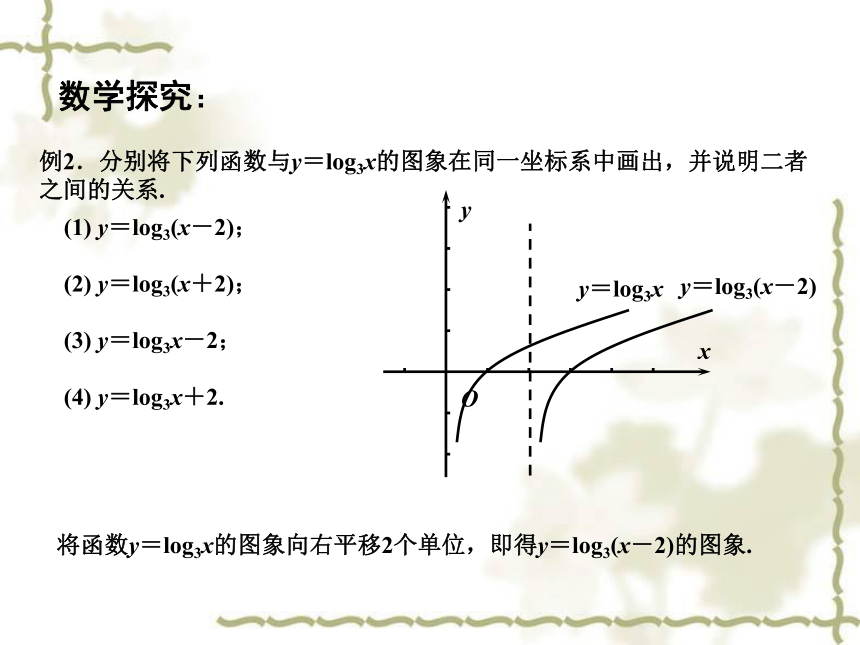
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
x
y
O
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
数学探究:
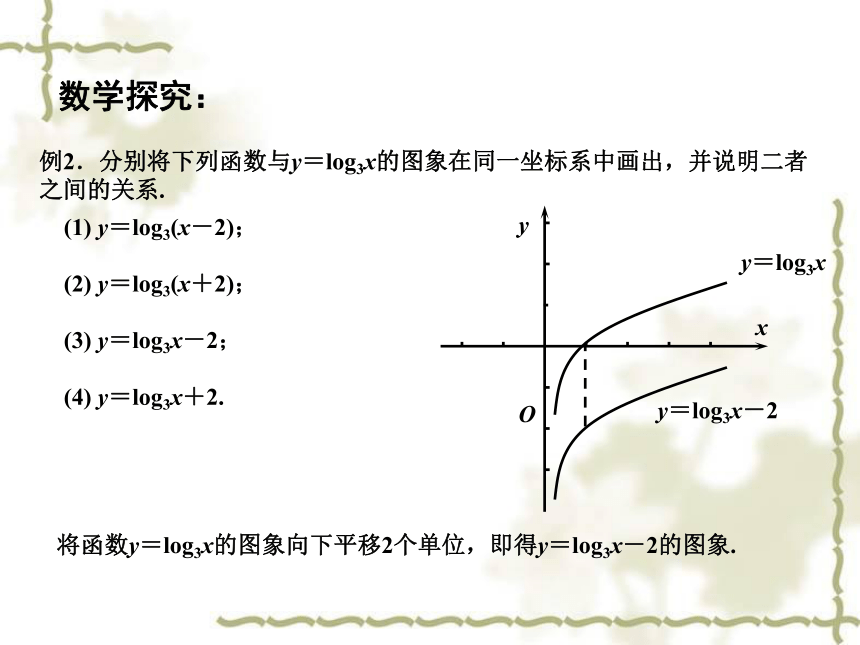
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
x
y
O
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
y=log3x
y=log3(x-2)
将函数y=log3x的图象向右平移2个单位,即得y=log3(x-2)的图象.
数学探究:
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
y=log3x
y=log3(x+2)
将函数y=log3x的图象向左平移2个单位,即得y=log3(x+2)的图象.
x
y
O
数学探究:
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
y=log3x
y=log3x-2
将函数y=log3x的图象向下平移2个单位,即得y=log3x-2的图象.
x
y
O
数学探究:
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
y=log3x
y=log3x+2
将函数y=log3x的图象向上平移2个单位,即得y=log3x+2的图象.
x
y
O
数学建构:
平移变换:
1.函数y=f(x)的图象与函数y=f(x+a)的图象关系为左右平移;
2.函数y=f(x)的图象与函数y=f(x)+a的图象关系为上下平移;
平移法则:左加右减,上加下减
数学应用:
x
y
O
(3)由函数y= log3(x+2),y =log3x的图象与直线y=-1,y=1所围成的封闭图形的面积是 .
(1)将函数y=logax的图像沿x轴向右平移2个单位,再向下平移1个单
位,所得函数图像的解析式 .
(2)对任意的实数a(a>0,a≠1),函数y=loga(x-1)+2的图像过的定点
坐标为 .
数学应用:
例3.画出函数y=log2|x|的图象.
x
y
O
结合函数y=log2|x|的图象,说出它的有关性质.
注:偶函数y=f(x)总可以写作y=f(|x|) .
说出函数y=log2(x-2)2的单调区间.
数学应用:
(1)画出函数y=|log2x|的图象.
结合图象讨论,写出该函数的单调区间.
x
y
O
试比较y=|log2x|的图象y=|log0.5x|的图象,说出二者的关系.
数学应用:
(2)在同一坐标系中,画出函数y=log2x与y=log2(-x)的图象,并说明二者之间关系.
x
y
O
将函数y=log2x的图象作关于y对称的图象,即为函数y=log2(-x)的图象.
y=log2x
y=log2(-x)
数学应用:
(3)在同一坐标系中,画出函数y=log2x与y=-log2x的图象,并说明二者之间关系.
x
y
O
将函数y=log2x的图象作关于x对称的图象,即为函数y=-log2x的图象.
y=log2x
y=-log2x
数学建构:
对称变换:
完全对称变换
1.函数y=f(x)的图象与函数y=-f(x)的图象关于x轴对称;
2.函数y=f(x)的图象与函数y=f(-x)的图象关于y轴对称;
3.函数y=f(x)的图象与到函数y=-f(-x)的图象关于原点对称.
局部对称变换
1.y=|f(x)|的图象是保留函数y=f(x)的图象上位于x轴上方部分,
而将位于x轴下方部分作关于x轴对称变换;
2.函数y=f(|x|)的图象是保留y=f(x)的图象上位于y轴右侧部分,
而将位于y轴右侧部分作关于y轴对称变换;
注:任一偶函数y=f(x)都可以表示为y=f(|x|)形式.
数学应用:
画出函数y=|log2x-1|的图象.
x
y
O
说明函数y= log2 的图象与函数y= log2x图象的关系.
小结:
平移变换:
对称变换:
掌握基本图形,掌握变换规律.
构造复杂函数的图象,能利用函数的图象揭示函数的性质.
作业:
P70习题2.3(2)6,8,9.
高中数学 必修1
情境问题:
对数函数的定义:
函数y=logax (a>0,a≠1)叫做对数函数.
对数函数的定义域为(0,+ ),值域为R .
对数函数的图象和性质:
对数函数的图象恒过点(1,0),
当0<a<1时,对数函数在(0,+ ) 上递减;
当a>1时,对数函数在(0,+ )上递增.
如图所示曲线是对数函数y=logax的图像,
已知a值取1.5,e,0.5,0.2,则相应于C1,C2,
C3,C4的a的值依次为 .
1
O
y
x
C1
C2
C3
C4
数学应用:
例1 .如图所示曲线是对数函数y=logax的图像,已知a值取0.2,0.5, 1.5,e,则相应于C1,C2,C3,C4的a的值依次为 .
1
O
y
x
C1
C2
C3
C4
数学探究:
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
x
y
O
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
数学探究:
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
x
y
O
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
y=log3x
y=log3(x-2)
将函数y=log3x的图象向右平移2个单位,即得y=log3(x-2)的图象.
数学探究:
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
y=log3x
y=log3(x+2)
将函数y=log3x的图象向左平移2个单位,即得y=log3(x+2)的图象.
x
y
O
数学探究:
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
y=log3x
y=log3x-2
将函数y=log3x的图象向下平移2个单位,即得y=log3x-2的图象.
x
y
O
数学探究:
例2.分别将下列函数与y=log3x的图象在同一坐标系中画出,并说明二者之间的关系.
(1) y=log3(x-2);
(2) y=log3(x+2);
(3) y=log3x-2;
(4) y=log3x+2.
y=log3x
y=log3x+2
将函数y=log3x的图象向上平移2个单位,即得y=log3x+2的图象.
x
y
O
数学建构:
平移变换:
1.函数y=f(x)的图象与函数y=f(x+a)的图象关系为左右平移;
2.函数y=f(x)的图象与函数y=f(x)+a的图象关系为上下平移;
平移法则:左加右减,上加下减
数学应用:
x
y
O
(3)由函数y= log3(x+2),y =log3x的图象与直线y=-1,y=1所围成的封闭图形的面积是 .
(1)将函数y=logax的图像沿x轴向右平移2个单位,再向下平移1个单
位,所得函数图像的解析式 .
(2)对任意的实数a(a>0,a≠1),函数y=loga(x-1)+2的图像过的定点
坐标为 .
数学应用:
例3.画出函数y=log2|x|的图象.
x
y
O
结合函数y=log2|x|的图象,说出它的有关性质.
注:偶函数y=f(x)总可以写作y=f(|x|) .
说出函数y=log2(x-2)2的单调区间.
数学应用:
(1)画出函数y=|log2x|的图象.
结合图象讨论,写出该函数的单调区间.
x
y
O
试比较y=|log2x|的图象y=|log0.5x|的图象,说出二者的关系.
数学应用:
(2)在同一坐标系中,画出函数y=log2x与y=log2(-x)的图象,并说明二者之间关系.
x
y
O
将函数y=log2x的图象作关于y对称的图象,即为函数y=log2(-x)的图象.
y=log2x
y=log2(-x)
数学应用:
(3)在同一坐标系中,画出函数y=log2x与y=-log2x的图象,并说明二者之间关系.
x
y
O
将函数y=log2x的图象作关于x对称的图象,即为函数y=-log2x的图象.
y=log2x
y=-log2x
数学建构:
对称变换:
完全对称变换
1.函数y=f(x)的图象与函数y=-f(x)的图象关于x轴对称;
2.函数y=f(x)的图象与函数y=f(-x)的图象关于y轴对称;
3.函数y=f(x)的图象与到函数y=-f(-x)的图象关于原点对称.
局部对称变换
1.y=|f(x)|的图象是保留函数y=f(x)的图象上位于x轴上方部分,
而将位于x轴下方部分作关于x轴对称变换;
2.函数y=f(|x|)的图象是保留y=f(x)的图象上位于y轴右侧部分,
而将位于y轴右侧部分作关于y轴对称变换;
注:任一偶函数y=f(x)都可以表示为y=f(|x|)形式.
数学应用:
画出函数y=|log2x-1|的图象.
x
y
O
说明函数y= log2 的图象与函数y= log2x图象的关系.
小结:
平移变换:
对称变换:
掌握基本图形,掌握变换规律.
构造复杂函数的图象,能利用函数的图象揭示函数的性质.
作业:
P70习题2.3(2)6,8,9.
