苏教版高中数学必修1课件 2.5.2 用二分法求方程的近似解(2)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.5.2 用二分法求方程的近似解(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 116.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 00:00:00 | ||
图片预览



文档简介
(共11张PPT)
高中数学 必修1
情境问题:
函数存在零点的判定:
若函数y=f (x)在区间[a,b]上的图象是一条不间断的曲线,
且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)上有零点.
二分法求函数的近似解:
对于在区间[a,b]上不间断,且满足f (a)·f (b) <0的函数y=f (x),通过不断地把函数f (x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
二分法求方程近似解的前提是确定根存在的区间,如何能迅速地确定区间(a,b)呢?
数学建构:
方程解的几何解释:
方程f(x)=g(x)的解,就是函数y=f(x)的图象与y=g(x)的图象交点的横坐标.
方程f(x)=g(x)的解,就是函数y=f(x)的图象与y=g(x)的图象交点的横坐标.利用两个函数的图象,可精略地估算出方程f(x)=g(x)的近似解,这就是图象法解方程.
注:
(1)在精确度要求不高时,可用图象法求解;
(2)在精确度要求较高时,先用图象法确定解存在的区间,再用二分法求
解.
图象法求方程的近似解 :
数学探究:
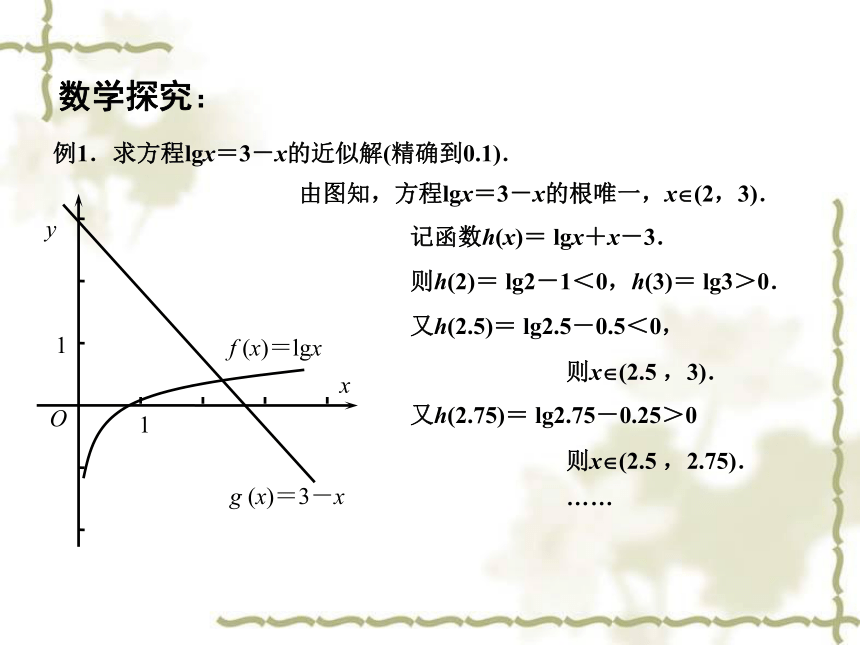
例1.求方程lgx=3-x的近似解(精确到0.1).
1
y
O
1
x
g (x)=3-x
f (x)=lgx
由图知,方程lgx=3-x的根唯一,x (2,3).
记函数h(x)= lgx+x-3.
则h(2)= lg2-1<0,h(3)= lg3>0.
又h(2.5)= lg2.5-0.5<0,
则x (2.5 ,3).
又h(2.75)= lg2.75-0.25>0
则x (2.5 ,2.75).
……
数学探究:
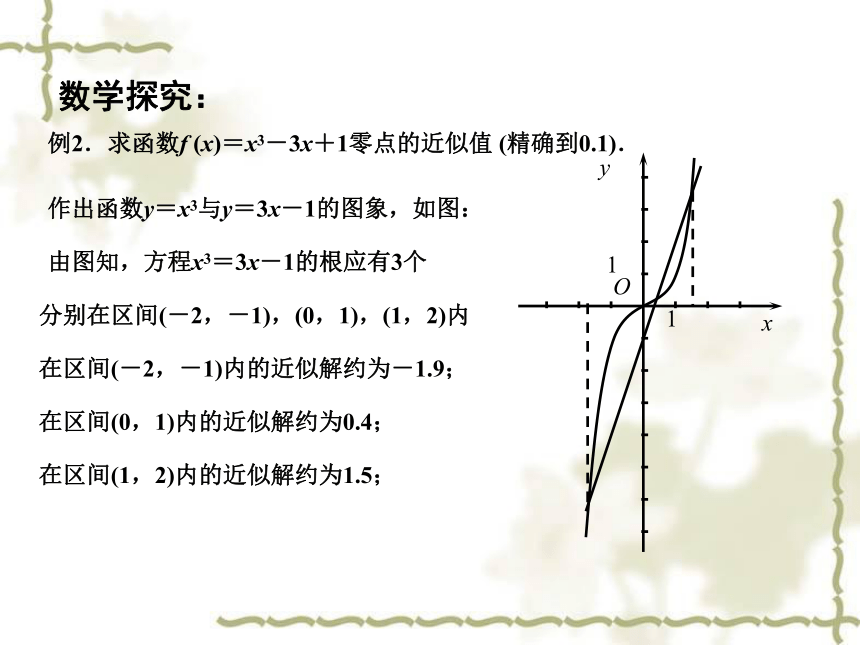
例2.求函数f (x)=x3-3x+1零点的近似值 (精确到0.1).
作出函数y=x3与y=3x-1的图象,如图:
1
y
O
1
x
由图知,方程x3=3x-1的根应有3个
分别在区间(-2,-1),(0,1),(1,2)内
在区间(-2,-1)内的近似解约为-1.9;
在区间(0,1)内的近似解约为0.4;
在区间(1,2)内的近似解约为1.5;
数学应用:
例3.在同一坐标系内分别画出函数f (x)=2x与g(x)=4-x的图象,并根据图象确定方程2x+x=4解存在的区间(区间长度为1).最后利用计算器,求出方程2x+x=4的近似解(精确到0.1).
数学建构:
数形结合:
数形结合思想是一种很重要的数学思想,数与形是事物的两个方面,正是基于对数与形的抽象研究才产生了数学这门学科,才能使人们能够
从不同侧面认识事物,华罗庚先生说过:“数与形本是两依倚,焉能分
作两边飞.数缺形时少直观,形少数时难入微。”把数量关系的研究转
化为图形性质的研究,或者把图形性质的研究转化为数量关系的研究,
这种解决问题过程中“数”与“形”相互转化的研究策略,就是数形结
合的思想。数形结合思想就是要使抽象的数学语言与直观的图形结合起
来,使抽象思维与形象思维结合起来.
在使用的过程中,由“形”到“数”的转化,往往比较明显,而由“数”到“形”的转化却需要转化的意识,因此,数形结合的思想的使用往往偏重于由“数”到“形”的转化.
数学应用:
方程lgx=x-5的根在区间(a,a+1)内,则正整数a= .再结合二分法,得lgx=x-5的近似解约为 (精确到0.1).
数学应用:
用不同的方法解方程2x2=3x-1.
小结:
图象法求方程的近似解.
数形结合.
作业:
P81练习第1题.
高中数学 必修1
情境问题:
函数存在零点的判定:
若函数y=f (x)在区间[a,b]上的图象是一条不间断的曲线,
且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)上有零点.
二分法求函数的近似解:
对于在区间[a,b]上不间断,且满足f (a)·f (b) <0的函数y=f (x),通过不断地把函数f (x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
二分法求方程近似解的前提是确定根存在的区间,如何能迅速地确定区间(a,b)呢?
数学建构:
方程解的几何解释:
方程f(x)=g(x)的解,就是函数y=f(x)的图象与y=g(x)的图象交点的横坐标.
方程f(x)=g(x)的解,就是函数y=f(x)的图象与y=g(x)的图象交点的横坐标.利用两个函数的图象,可精略地估算出方程f(x)=g(x)的近似解,这就是图象法解方程.
注:
(1)在精确度要求不高时,可用图象法求解;
(2)在精确度要求较高时,先用图象法确定解存在的区间,再用二分法求
解.
图象法求方程的近似解 :
数学探究:
例1.求方程lgx=3-x的近似解(精确到0.1).
1
y
O
1
x
g (x)=3-x
f (x)=lgx
由图知,方程lgx=3-x的根唯一,x (2,3).
记函数h(x)= lgx+x-3.
则h(2)= lg2-1<0,h(3)= lg3>0.
又h(2.5)= lg2.5-0.5<0,
则x (2.5 ,3).
又h(2.75)= lg2.75-0.25>0
则x (2.5 ,2.75).
……
数学探究:
例2.求函数f (x)=x3-3x+1零点的近似值 (精确到0.1).
作出函数y=x3与y=3x-1的图象,如图:
1
y
O
1
x
由图知,方程x3=3x-1的根应有3个
分别在区间(-2,-1),(0,1),(1,2)内
在区间(-2,-1)内的近似解约为-1.9;
在区间(0,1)内的近似解约为0.4;
在区间(1,2)内的近似解约为1.5;
数学应用:
例3.在同一坐标系内分别画出函数f (x)=2x与g(x)=4-x的图象,并根据图象确定方程2x+x=4解存在的区间(区间长度为1).最后利用计算器,求出方程2x+x=4的近似解(精确到0.1).
数学建构:
数形结合:
数形结合思想是一种很重要的数学思想,数与形是事物的两个方面,正是基于对数与形的抽象研究才产生了数学这门学科,才能使人们能够
从不同侧面认识事物,华罗庚先生说过:“数与形本是两依倚,焉能分
作两边飞.数缺形时少直观,形少数时难入微。”把数量关系的研究转
化为图形性质的研究,或者把图形性质的研究转化为数量关系的研究,
这种解决问题过程中“数”与“形”相互转化的研究策略,就是数形结
合的思想。数形结合思想就是要使抽象的数学语言与直观的图形结合起
来,使抽象思维与形象思维结合起来.
在使用的过程中,由“形”到“数”的转化,往往比较明显,而由“数”到“形”的转化却需要转化的意识,因此,数形结合的思想的使用往往偏重于由“数”到“形”的转化.
数学应用:
方程lgx=x-5的根在区间(a,a+1)内,则正整数a= .再结合二分法,得lgx=x-5的近似解约为 (精确到0.1).
数学应用:
用不同的方法解方程2x2=3x-1.
小结:
图象法求方程的近似解.
数形结合.
作业:
P81练习第1题.
