人教版数学八年级上册:12.2.6三角形全等的判定和性质综合应用 教案
文档属性
| 名称 | 人教版数学八年级上册:12.2.6三角形全等的判定和性质综合应用 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 15:30:36 | ||
图片预览

文档简介
人教版八年级上全等三角形教学设计
【教学目标】
一、知识与技能目标
复习全等三角形的概念、性质和判定方法,能够利用三角形全等性质和判定进行证明,巩固综合法证明的格式。
二、过程与方法目标
进一步练习有理有据的推理证明、精炼准确地表达推理过程,注重分析思路,学会思考问题,注重书写格式,学会清楚地表达思考的过程。
三、情感态度与价值观目标
培养逻辑思维能力,发展基本的创新意识和能力,培养并提高学生归纳,对比及分析问题,解决问题的能力,激发学生的学习兴趣,养成勤于思考的好习惯.
教学重点:全等三角形的性质和判定方法.
教学难点:1、了解全等三角形的概念,能识别全等三角形中的对应边、对应角;
2、理解全等三角形的性质,掌握两个三角形全等的条件;
3、会用全等三角形的进行角、线段的有关计算和证明。.
教学过程:
知识框架回顾
图形的全等:能够完全重合大小,形状相同
全等三角形性质:
对应边、角相等,对应周长、面积相等
全等三角形性判定:SSS、ASA、SAS、AAS、HL
问题引出
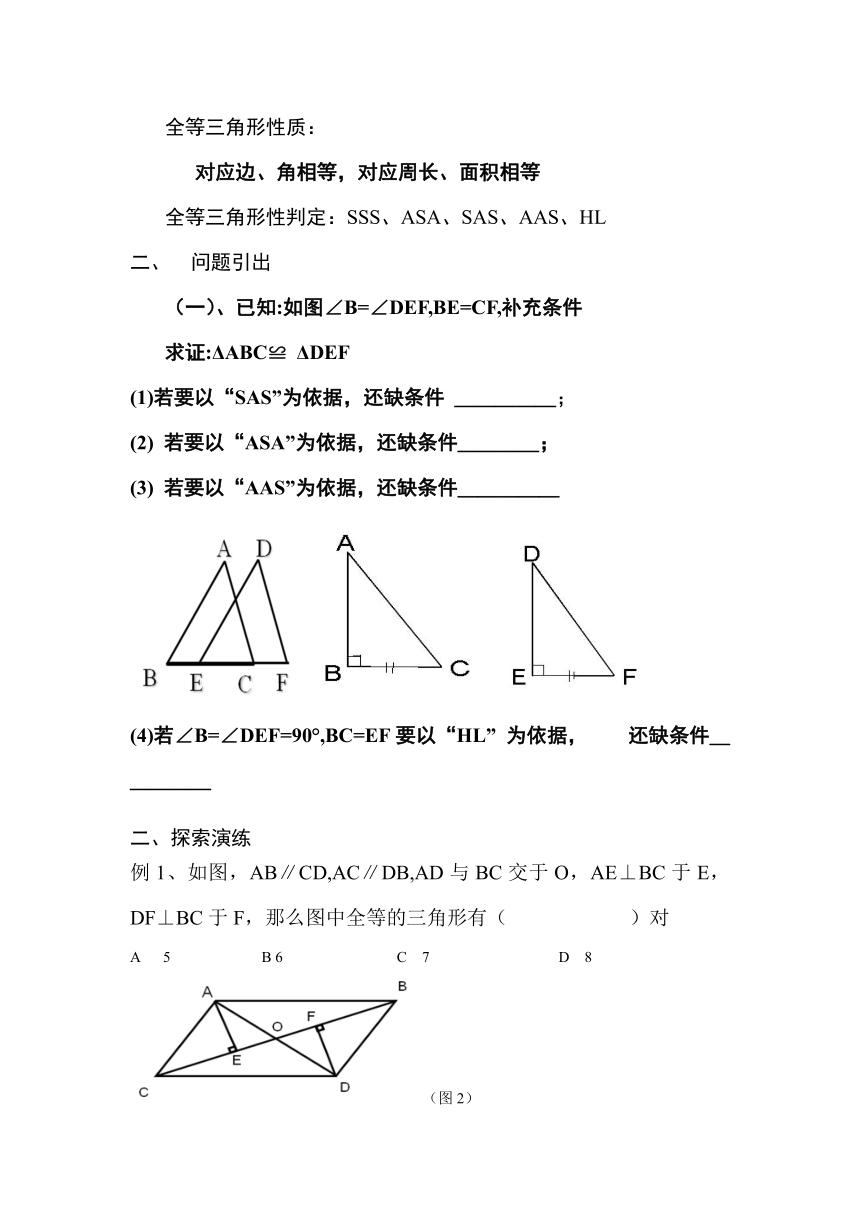
(一)、已知:如图∠B=∠DEF,BE=CF,补充条件
求证:ΔABC≌ ΔDEF
(1)若要以“SAS”为依据,还缺条件 _____;
(2) 若要以“ASA”为依据,还缺条件____;
(3) 若要以“AAS”为依据,还缺条件_____
(4)若∠B=∠DEF=90°,BC=EF要以“HL” 为依据, 还缺条件_____
二、探索演练
例1、如图,AB∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )对
A 5 B 6 C 7 D 8
(图2)
(采用合作探究的学习方式探索例题,锻炼学生的探索精神,提升学生的思维能力)
变式训练:
1、如图3, 已知∠A =∠C,∠B =∠D, 要使△ABO≌△CDO,需要补充的一个 条件是 _____
(图4)
2、如图4,△ACE≌△DBF,若∠E =∠F, AD = 8,BC = 2,则AB等于( )
3、如图,已知AD=AB, 要使 需要添加一个条件是( )
三、拓展应用
例2:如图,已知△ABC中,BE和CD分别为 ∠ABC和∠ACB的平分线,且BD = CE,∠1 = ∠2。说明BE = CD的理由。
解:∵∠DBC = 2∠1,∠ECB = 2∠2
(角平分线的定义)
∴ ∠1 = ∠2,∠DBC = ∠ECB
在△DBC和△ECB中
BD = CE(已知)
∠DBC = ∠ECB
BC = CB(公共边)
∴ △DBC≌△ECB(SAS)
∴BE = CD(全等三角形的对应边相等)
四、练习巩固
如图,AC和BD相交于点O, OA=OC, OB=OD , 求证:DC∥AB
证明:在△ABO和△CDO中
OA=OC
∠AOB= ∠COD
OB=OD
∴ △ABO≌△CDO (SAS)
∴ ∠A= ∠C
∴ DC∥AB
五、课堂小结
五、作业布置
1、检测题
2、中考总复习 P51~53
六、板书设计
全等三角形总复习
性质:对应边、角相等,对应周长、面积相等
判定:SSS、ASA、SAS、AAS、HL
【教学目标】
一、知识与技能目标
复习全等三角形的概念、性质和判定方法,能够利用三角形全等性质和判定进行证明,巩固综合法证明的格式。
二、过程与方法目标
进一步练习有理有据的推理证明、精炼准确地表达推理过程,注重分析思路,学会思考问题,注重书写格式,学会清楚地表达思考的过程。
三、情感态度与价值观目标
培养逻辑思维能力,发展基本的创新意识和能力,培养并提高学生归纳,对比及分析问题,解决问题的能力,激发学生的学习兴趣,养成勤于思考的好习惯.
教学重点:全等三角形的性质和判定方法.
教学难点:1、了解全等三角形的概念,能识别全等三角形中的对应边、对应角;
2、理解全等三角形的性质,掌握两个三角形全等的条件;
3、会用全等三角形的进行角、线段的有关计算和证明。.
教学过程:
知识框架回顾
图形的全等:能够完全重合大小,形状相同
全等三角形性质:
对应边、角相等,对应周长、面积相等
全等三角形性判定:SSS、ASA、SAS、AAS、HL
问题引出
(一)、已知:如图∠B=∠DEF,BE=CF,补充条件
求证:ΔABC≌ ΔDEF
(1)若要以“SAS”为依据,还缺条件 _____;
(2) 若要以“ASA”为依据,还缺条件____;
(3) 若要以“AAS”为依据,还缺条件_____
(4)若∠B=∠DEF=90°,BC=EF要以“HL” 为依据, 还缺条件_____
二、探索演练
例1、如图,AB∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )对
A 5 B 6 C 7 D 8
(图2)
(采用合作探究的学习方式探索例题,锻炼学生的探索精神,提升学生的思维能力)
变式训练:
1、如图3, 已知∠A =∠C,∠B =∠D, 要使△ABO≌△CDO,需要补充的一个 条件是 _____
(图4)
2、如图4,△ACE≌△DBF,若∠E =∠F, AD = 8,BC = 2,则AB等于( )
3、如图,已知AD=AB, 要使 需要添加一个条件是( )
三、拓展应用
例2:如图,已知△ABC中,BE和CD分别为 ∠ABC和∠ACB的平分线,且BD = CE,∠1 = ∠2。说明BE = CD的理由。
解:∵∠DBC = 2∠1,∠ECB = 2∠2
(角平分线的定义)
∴ ∠1 = ∠2,∠DBC = ∠ECB
在△DBC和△ECB中
BD = CE(已知)
∠DBC = ∠ECB
BC = CB(公共边)
∴ △DBC≌△ECB(SAS)
∴BE = CD(全等三角形的对应边相等)
四、练习巩固
如图,AC和BD相交于点O, OA=OC, OB=OD , 求证:DC∥AB
证明:在△ABO和△CDO中
OA=OC
∠AOB= ∠COD
OB=OD
∴ △ABO≌△CDO (SAS)
∴ ∠A= ∠C
∴ DC∥AB
五、课堂小结
五、作业布置
1、检测题
2、中考总复习 P51~53
六、板书设计
全等三角形总复习
性质:对应边、角相等,对应周长、面积相等
判定:SSS、ASA、SAS、AAS、HL
