苏教版高中数学必修1课件 2.6 函数模型及其应用(2)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.6 函数模型及其应用(2) |  | |
| 格式 | rar | ||
| 文件大小 | 127.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 09:18:53 | ||
图片预览




文档简介
(共14张PPT)
高中数学 必修1
情境创设:
已知矩形的长为4、宽为3,如果长增加x,宽减少0.5x,所得新矩形的面积为S.
(1)将S表示成x的函数;
(2)求面积S的最大值,并求此时x的值.
涉及几何图形的问题也是数学建模问题中常见题型.
数学应用:
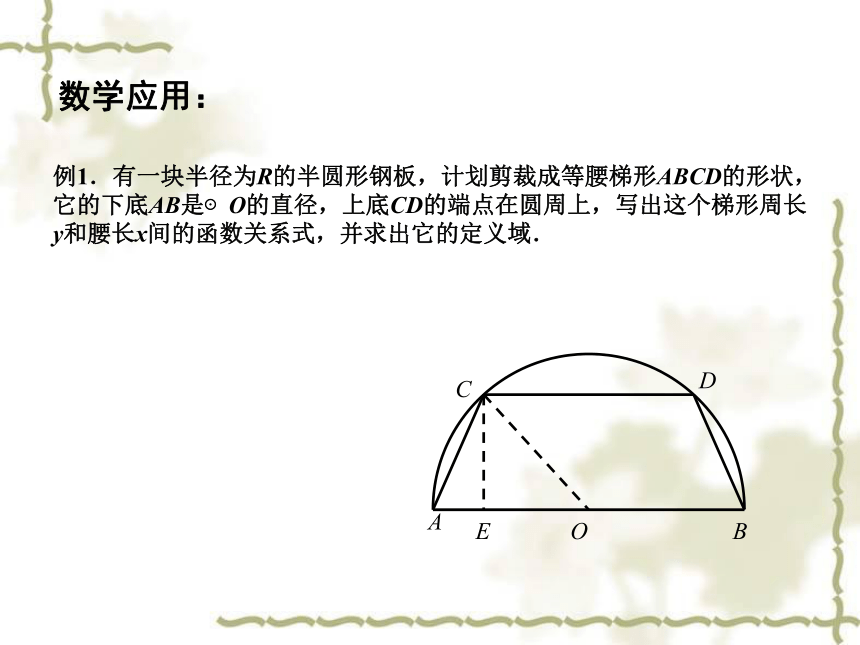
例1.有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形周长y和腰长x间的函数关系式,并求出它的定义域.
A
B
O
C
D
E
数学应用:
x
t
O
A
B
C
y
l
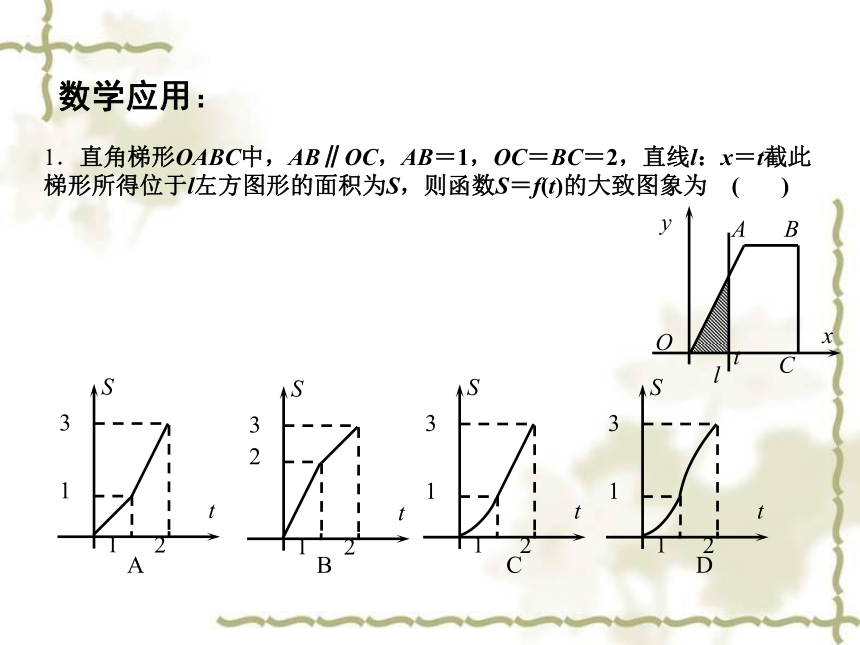
1.直角梯形OABC中,AB∥OC,AB=1,OC=BC=2,直线l:x=t截此梯形所得位于l左方图形的面积为S,则函数S=f(t)的大致图象为 ( )
t
S
A
B
C
D
1
2
1
3
t
S
1
2
2
3
t
S
1
2
1
3
t
S
1
2
1
3
数学应用:
2.一个圆柱形容器的底部直径是dcm,高是hcm,现在以vcm3/s的速度向容器内注入某种溶液,求容器内溶液的高度x(cm)与注入溶液的时间t(s)之间的函数关系式,并写出函数的定义域.
3.向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状可能是( )
h
V
H
数学应用:
要使每天收入最高,每间客房定价为 .
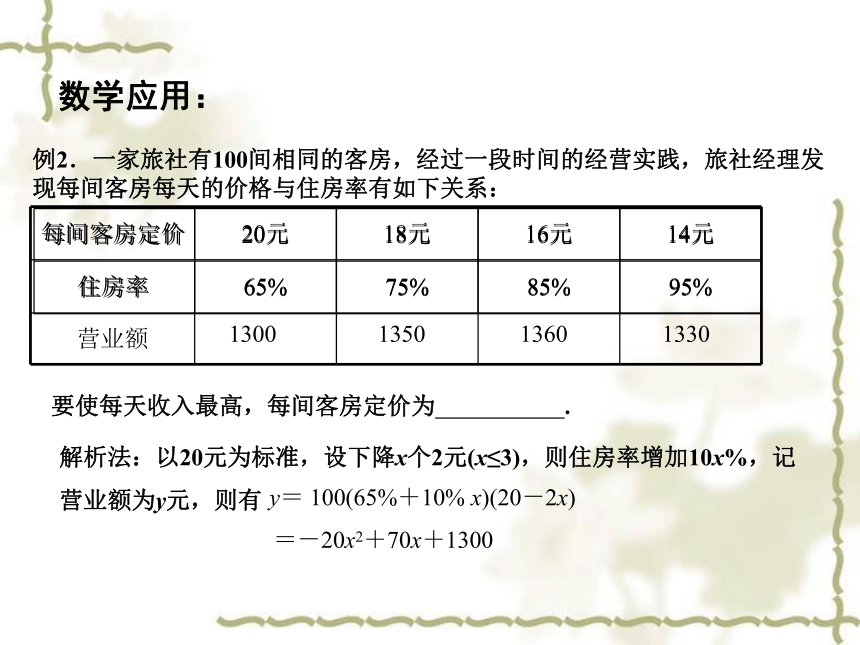
例2.一家旅社有100间相同的客房,经过一段时间的经营实践,旅社经理发现每间客房每天的价格与住房率有如下关系:
每间客房定价 20元 18元 16元 14元
住房率 65% 75% 85% 95%
每间客房定价 20元 18元 16元 14元
住房率 65% 75% 85% 95%
营业额
1300
1350
1360
1330
解析法:以20元为标准,设下降x个2元(x≤3),则住房率增加10x%,记
营业额为y元,则有
y= 100(65%+10% x)(20-2x)
=-20x2+70x+1300
数学应用:
4.某公司将进货单价为10元一个的商品按13元一个销售,每天可卖200个.
若这种商品每涨价1元,销售量则减少26个.
(1)售价为15元时,销售利润为多少?
(2)若销售价必须为整数,要使利润最大,应如何定价?
数学应用:
5.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车就增加1辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金为3600元时,能租出多少辆车
(2)当每辆车的月租金为多少元时,公司的月收益最大 最大月收益是多少元
数学应用:
例3.今年5月,荔枝上市.由历年的市场行情得知,从5月10日起的60天内,荔枝的市场售价与上市时间的关系大致可用如图所示的折线ABCD表示(市场售价的单位为元/500g).
请写出市场售价S(t)(元)与上市时间t(天)的函数关系式,并求出6月20日当天的荔枝市场售价.
A
B
C
D
O
5
7
10
10
40
60
t(天)
S(元)
数学应用:
6.根据市场调查,某商品在最近40天内的价格f(t)与时间t满足:
f(t)= 销售量g(t)与时间t满足:g(t)=
(0≤t≤40,t N),求这种商品日销售金额的最大值.
(0≤t≤40,t N),
-t+41 (0≤t≤40,t N),
7.一批材料可以建成200m长的围墙,现用这些材料在一边靠墙的地方围成一块矩形场地,中间隔成3个相等的的矩形,则围成的矩形的最大面积为 m2.
数学应用:
数学应用:
8.我国是水资源比较贫乏的国家之一,各地采用价格调控手段以达到节约用水的目的.某市收水费方法是:水费=基本费+超额费+损耗费.该市规定:(1)若每户每月用水量不超过最低限量m立方米时,只付基本费9元和每月的定额损耗费a元;(2)若每户每月用水量超过立方米时,除了付基本费和损耗费外,超过部分每立方米付n元的超额费;(3)每户每月的损耗费不超过5元.
(I)求每户月水费y(元)与月用水量x(立方米)的函数关系;
(II)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示,试分析一、二、三各月份的用水量是否超过最低限量,并求m,n,a的值.
月份 用水量(立方米) 水费(元)
一 4 18
二 5 26
三 2.5 10
小结:
确立数学模型
解出模型结果
解释实际问题
实际问题
作业:
P93第4,16题.
高中数学 必修1
情境创设:
已知矩形的长为4、宽为3,如果长增加x,宽减少0.5x,所得新矩形的面积为S.
(1)将S表示成x的函数;
(2)求面积S的最大值,并求此时x的值.
涉及几何图形的问题也是数学建模问题中常见题型.
数学应用:
例1.有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形周长y和腰长x间的函数关系式,并求出它的定义域.
A
B
O
C
D
E
数学应用:
x
t
O
A
B
C
y
l
1.直角梯形OABC中,AB∥OC,AB=1,OC=BC=2,直线l:x=t截此梯形所得位于l左方图形的面积为S,则函数S=f(t)的大致图象为 ( )
t
S
A
B
C
D
1
2
1
3
t
S
1
2
2
3
t
S
1
2
1
3
t
S
1
2
1
3
数学应用:
2.一个圆柱形容器的底部直径是dcm,高是hcm,现在以vcm3/s的速度向容器内注入某种溶液,求容器内溶液的高度x(cm)与注入溶液的时间t(s)之间的函数关系式,并写出函数的定义域.
3.向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状可能是( )
h
V
H
数学应用:
要使每天收入最高,每间客房定价为 .
例2.一家旅社有100间相同的客房,经过一段时间的经营实践,旅社经理发现每间客房每天的价格与住房率有如下关系:
每间客房定价 20元 18元 16元 14元
住房率 65% 75% 85% 95%
每间客房定价 20元 18元 16元 14元
住房率 65% 75% 85% 95%
营业额
1300
1350
1360
1330
解析法:以20元为标准,设下降x个2元(x≤3),则住房率增加10x%,记
营业额为y元,则有
y= 100(65%+10% x)(20-2x)
=-20x2+70x+1300
数学应用:
4.某公司将进货单价为10元一个的商品按13元一个销售,每天可卖200个.
若这种商品每涨价1元,销售量则减少26个.
(1)售价为15元时,销售利润为多少?
(2)若销售价必须为整数,要使利润最大,应如何定价?
数学应用:
5.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车就增加1辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金为3600元时,能租出多少辆车
(2)当每辆车的月租金为多少元时,公司的月收益最大 最大月收益是多少元
数学应用:
例3.今年5月,荔枝上市.由历年的市场行情得知,从5月10日起的60天内,荔枝的市场售价与上市时间的关系大致可用如图所示的折线ABCD表示(市场售价的单位为元/500g).
请写出市场售价S(t)(元)与上市时间t(天)的函数关系式,并求出6月20日当天的荔枝市场售价.
A
B
C
D
O
5
7
10
10
40
60
t(天)
S(元)
数学应用:
6.根据市场调查,某商品在最近40天内的价格f(t)与时间t满足:
f(t)= 销售量g(t)与时间t满足:g(t)=
(0≤t≤40,t N),求这种商品日销售金额的最大值.
(0≤t≤40,t N),
-t+41 (0≤t≤40,t N),
7.一批材料可以建成200m长的围墙,现用这些材料在一边靠墙的地方围成一块矩形场地,中间隔成3个相等的的矩形,则围成的矩形的最大面积为 m2.
数学应用:
数学应用:
8.我国是水资源比较贫乏的国家之一,各地采用价格调控手段以达到节约用水的目的.某市收水费方法是:水费=基本费+超额费+损耗费.该市规定:(1)若每户每月用水量不超过最低限量m立方米时,只付基本费9元和每月的定额损耗费a元;(2)若每户每月用水量超过立方米时,除了付基本费和损耗费外,超过部分每立方米付n元的超额费;(3)每户每月的损耗费不超过5元.
(I)求每户月水费y(元)与月用水量x(立方米)的函数关系;
(II)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示,试分析一、二、三各月份的用水量是否超过最低限量,并求m,n,a的值.
月份 用水量(立方米) 水费(元)
一 4 18
二 5 26
三 2.5 10
小结:
确立数学模型
解出模型结果
解释实际问题
实际问题
作业:
P93第4,16题.
