苏教版高中数学必修1课件 2.6 函数模型及其应用(3)
文档属性
| 名称 | 苏教版高中数学必修1课件 2.6 函数模型及其应用(3) |  | |
| 格式 | rar | ||
| 文件大小 | 159.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-02 09:18:53 | ||
图片预览





文档简介
(共18张PPT)
高中数学 必修1
情境问题:
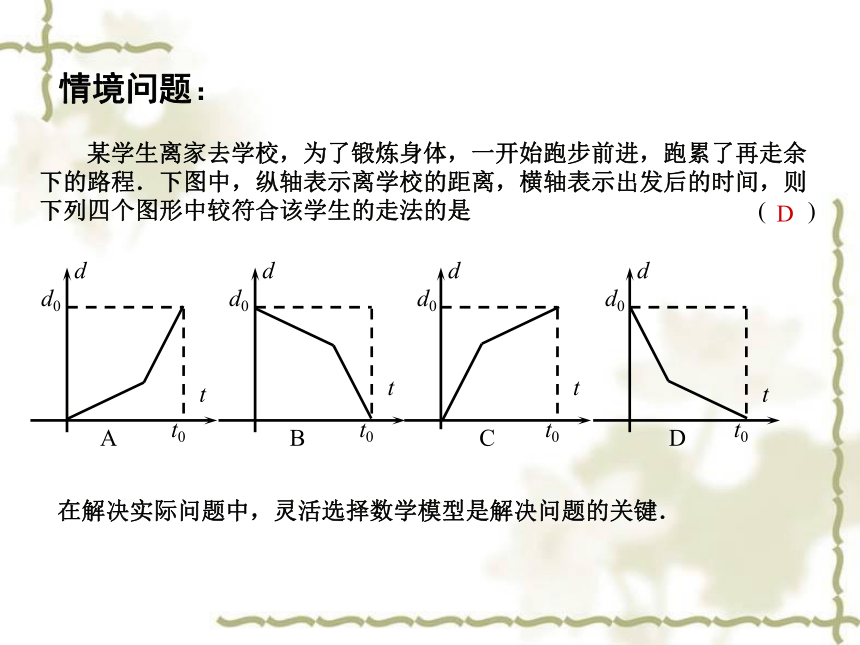
某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程.下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该学生的走法的是 ( )
t
d
d0
t0
t
d
d0
t0
t
d
d0
t0
t
d
d0
t0
A
B
C
D
D
在解决实际问题中,灵活选择数学模型是解决问题的关键.
情境问题:
某工厂第一季度某产品月产量分别为1万件、1.2万件、1.3万件.为了估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系.模拟函数可以选用二次函数或函数y=a·bx+c(其中a,b,c为常数).已知4月份的产量为1.36万件,问:用以上哪个函数作为模拟函数好?为什么?
数学建构:
1.数据的拟合.
数据拟合就是研究变量之间这种关系,并给出近似的数学表达式的一种方法.根据拟合模型,我们还可以对某变量进行预测或控制.解决数据拟合问题应首先作出散点图,然后通过观察散点趋势选用相应的模型进行拟合.为使散点图更为清晰,可将数据适当简化.
2.函数模型的选择.
(1)直线型函数——一次函数
(2)对称型函数——二次函数
(3)单调型函数——指数型函数
反比例幂型函数
y=k·ax+b或
数学应用:
例1.现有一杯用88℃热水冲的速溶咖啡,放在24℃的房间中,如果咖啡降温到40℃需要20min,那么降温到32℃时,需要多长时间;降温到36℃时,需要多长时间(结果精确到0.1) ?
物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始
温度是T0,经过一定时间t后的温度是T,
其中Ta表示环境温度, h称为半衰期.
数学探究:
例2.在经济学中,函数f(x)的边际函数Mf(x)的定义为Mf(x)= f(x+1) - f(x),某公司每月最多生长100台报警系统装置,生产x台(x N*)的收入为 R(x)=3000x-20x2(单位:元),其成本函数为C(x)=500x+4000(单位:元),利润是收入与成本之差.
(1)求利润函数P(x)及边际利润函数MP(x);
(2)利润函数P(x)与边际利润函数MP(x)是否有相同的最大值?
边际函数是经济学中的一个基本概念,也是通过大量的数据拟合,从中筛选出恰当的数学模型,从而使得经济学研究更加准确,决策更加科学.
情境问题:
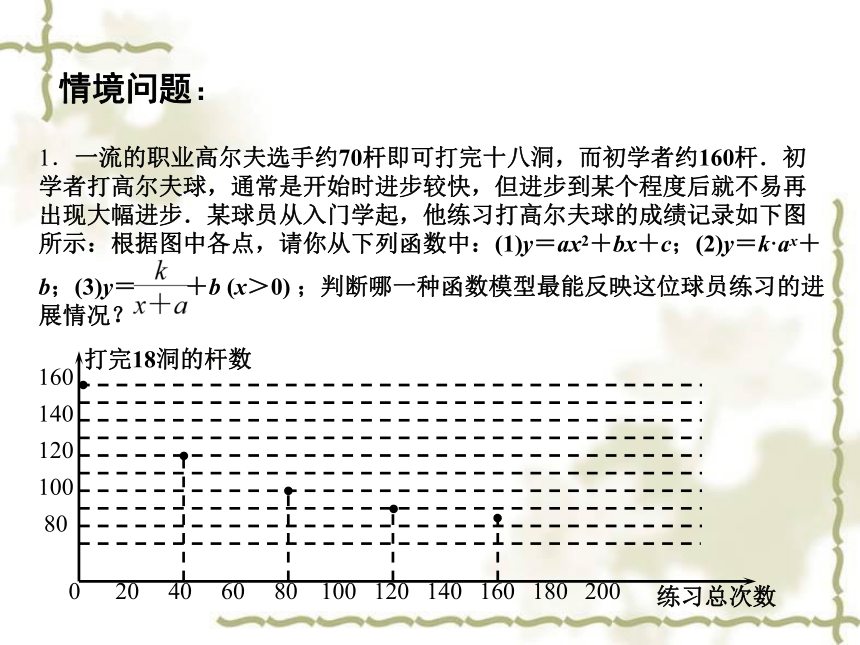
1.一流的职业高尔夫选手约70杆即可打完十八洞,而初学者约160杆.初学者打高尔夫球,通常是开始时进步较快,但进步到某个程度后就不易再出现大幅进步.某球员从入门学起,他练习打高尔夫球的成绩记录如下图所示:根据图中各点,请你从下列函数中:(1)y=ax2+bx+c;(2)y=k·ax+
b;(3)y= +b (x>0) ;判断哪一种函数模型最能反映这位球员练习的进展情况?
0
20
40
60
80
100
120
140
160
180
200
80
100
120
140
160
练习总次数
打完18洞的杆数
0
20
40
60
80
100
120
140
160
180
200
80
100
120
140
160
练习总次数
打完18洞的杆数
y=ax2+bx+c
过(40,120),(80,100),(120, 90)三点的
数学探究:
二次函数的解析式为
0
20
40
60
80
100
120
140
160
180
200
80
100
120
140
160
练习总次数
打完18洞的杆数
y=k·ax+b
数学探究:
0
20
40
60
80
100
120
140
160
180
200
80
100
120
140
160
练习总次数
打完18洞的杆数
过(40,120),(80,100),(120, 90)三点的幂
型函数的解析式为
数学探究:
数学应用:
由
当x=200时,y≈83杆.
,得
因此至第200次练习时,打完十八洞估测约需要83杆.
综上所述,该问题选指数型函数进行拟合较好.
按照这种趋势,如果他不退步,至第200次练习时,打完十八洞估测
约多少杆?
数学应用:
在处理数据拟合(预测或控制)问题时,通常需要以下几个步骤:
(1)根据原始数据,在屏幕直角坐标系中绘出散点图;
(2)通过观察散点图,画出“最贴近”的曲线,即拟合曲线;
(3)根据所学知识,设出拟合曲线的函数解析式.
(4)利用此函数解析式,根据条件对所给的问题进行预测和控制.
数学应用:
例3.某工厂第一季度某产品月产量分别为1万件、1.2万件、1.3万件.为了估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系.模拟函数可以选用二次函数或函数y=a·bx+c(其中a,b,c为常数).已知4月份的产量为1.36万件,问:用以上哪个函数作为模拟函数好?为什么?
2.一家人(父亲、母亲、孩子)去某地旅游,有两空旅行社同时发出邀请,且有各自的优惠政策.甲旅行社承诺,只要父亲一人买全票,其他家庭成员均享受半价;乙旅行社承诺,家庭旅行算团体旅行,按全价的三分之二计算.已知这两家的原价是一样的,若家庭中的孩子数是不同的,试分别列出两家旅行社优惠政策实施后的孩子个数为变量的收费表达式,并比较选择哪家更优惠?
数学应用:
3.某化工厂生产的一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次可使杂质含量减少 ,问:至少应过滤几次才能使产品达到市场要求?
数学应用:
4.已知镭经过100年剩留原来质量的95.76%,试计算镭的半衰期?
数学应用:
5.某工厂的一种产品的年产量第二年比第一年增加21%,第三年比第二年增加44%,则这两年的平均增长率为 .
6.某乡镇现在人均一年占有粮食360千克,如果该乡镇人口平均每年增
长1.2%,粮食总产量平均每年增长4%,那么x年后若人均一年占有y千
克粮食,求出函数y关于x的解析式.
小结:
确立数学模型
解出模型结果
解释实际问题
实际问题
选择不同模型加以拟合
作业:
P88第4题.
高中数学 必修1
情境问题:
某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程.下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该学生的走法的是 ( )
t
d
d0
t0
t
d
d0
t0
t
d
d0
t0
t
d
d0
t0
A
B
C
D
D
在解决实际问题中,灵活选择数学模型是解决问题的关键.
情境问题:
某工厂第一季度某产品月产量分别为1万件、1.2万件、1.3万件.为了估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系.模拟函数可以选用二次函数或函数y=a·bx+c(其中a,b,c为常数).已知4月份的产量为1.36万件,问:用以上哪个函数作为模拟函数好?为什么?
数学建构:
1.数据的拟合.
数据拟合就是研究变量之间这种关系,并给出近似的数学表达式的一种方法.根据拟合模型,我们还可以对某变量进行预测或控制.解决数据拟合问题应首先作出散点图,然后通过观察散点趋势选用相应的模型进行拟合.为使散点图更为清晰,可将数据适当简化.
2.函数模型的选择.
(1)直线型函数——一次函数
(2)对称型函数——二次函数
(3)单调型函数——指数型函数
反比例幂型函数
y=k·ax+b或
数学应用:
例1.现有一杯用88℃热水冲的速溶咖啡,放在24℃的房间中,如果咖啡降温到40℃需要20min,那么降温到32℃时,需要多长时间;降温到36℃时,需要多长时间(结果精确到0.1) ?
物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始
温度是T0,经过一定时间t后的温度是T,
其中Ta表示环境温度, h称为半衰期.
数学探究:
例2.在经济学中,函数f(x)的边际函数Mf(x)的定义为Mf(x)= f(x+1) - f(x),某公司每月最多生长100台报警系统装置,生产x台(x N*)的收入为 R(x)=3000x-20x2(单位:元),其成本函数为C(x)=500x+4000(单位:元),利润是收入与成本之差.
(1)求利润函数P(x)及边际利润函数MP(x);
(2)利润函数P(x)与边际利润函数MP(x)是否有相同的最大值?
边际函数是经济学中的一个基本概念,也是通过大量的数据拟合,从中筛选出恰当的数学模型,从而使得经济学研究更加准确,决策更加科学.
情境问题:
1.一流的职业高尔夫选手约70杆即可打完十八洞,而初学者约160杆.初学者打高尔夫球,通常是开始时进步较快,但进步到某个程度后就不易再出现大幅进步.某球员从入门学起,他练习打高尔夫球的成绩记录如下图所示:根据图中各点,请你从下列函数中:(1)y=ax2+bx+c;(2)y=k·ax+
b;(3)y= +b (x>0) ;判断哪一种函数模型最能反映这位球员练习的进展情况?
0
20
40
60
80
100
120
140
160
180
200
80
100
120
140
160
练习总次数
打完18洞的杆数
0
20
40
60
80
100
120
140
160
180
200
80
100
120
140
160
练习总次数
打完18洞的杆数
y=ax2+bx+c
过(40,120),(80,100),(120, 90)三点的
数学探究:
二次函数的解析式为
0
20
40
60
80
100
120
140
160
180
200
80
100
120
140
160
练习总次数
打完18洞的杆数
y=k·ax+b
数学探究:
0
20
40
60
80
100
120
140
160
180
200
80
100
120
140
160
练习总次数
打完18洞的杆数
过(40,120),(80,100),(120, 90)三点的幂
型函数的解析式为
数学探究:
数学应用:
由
当x=200时,y≈83杆.
,得
因此至第200次练习时,打完十八洞估测约需要83杆.
综上所述,该问题选指数型函数进行拟合较好.
按照这种趋势,如果他不退步,至第200次练习时,打完十八洞估测
约多少杆?
数学应用:
在处理数据拟合(预测或控制)问题时,通常需要以下几个步骤:
(1)根据原始数据,在屏幕直角坐标系中绘出散点图;
(2)通过观察散点图,画出“最贴近”的曲线,即拟合曲线;
(3)根据所学知识,设出拟合曲线的函数解析式.
(4)利用此函数解析式,根据条件对所给的问题进行预测和控制.
数学应用:
例3.某工厂第一季度某产品月产量分别为1万件、1.2万件、1.3万件.为了估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系.模拟函数可以选用二次函数或函数y=a·bx+c(其中a,b,c为常数).已知4月份的产量为1.36万件,问:用以上哪个函数作为模拟函数好?为什么?
2.一家人(父亲、母亲、孩子)去某地旅游,有两空旅行社同时发出邀请,且有各自的优惠政策.甲旅行社承诺,只要父亲一人买全票,其他家庭成员均享受半价;乙旅行社承诺,家庭旅行算团体旅行,按全价的三分之二计算.已知这两家的原价是一样的,若家庭中的孩子数是不同的,试分别列出两家旅行社优惠政策实施后的孩子个数为变量的收费表达式,并比较选择哪家更优惠?
数学应用:
3.某化工厂生产的一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次可使杂质含量减少 ,问:至少应过滤几次才能使产品达到市场要求?
数学应用:
4.已知镭经过100年剩留原来质量的95.76%,试计算镭的半衰期?
数学应用:
5.某工厂的一种产品的年产量第二年比第一年增加21%,第三年比第二年增加44%,则这两年的平均增长率为 .
6.某乡镇现在人均一年占有粮食360千克,如果该乡镇人口平均每年增
长1.2%,粮食总产量平均每年增长4%,那么x年后若人均一年占有y千
克粮食,求出函数y关于x的解析式.
小结:
确立数学模型
解出模型结果
解释实际问题
实际问题
选择不同模型加以拟合
作业:
P88第4题.
