人教版数学九年级上册22.3.4水位变化教案
文档属性
| 名称 | 人教版数学九年级上册22.3.4水位变化教案 |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 23:48:57 | ||
图片预览

文档简介
22.3 实际问题与二次函数(第3课时)
【教学目标】
? ◆知识技能
??1.能够正确灵活地建立直角坐标系解决实际问题;
2.能综合利用方程、二次函数的知识解决实际问题。?
? ◆过程与方法
1. 让学生经历分析实际问题从而建立二次函数模型来解决问题的过程,体会数学建模的思想.
2.体会数学与现实生活的紧密联系,增强应用意识,提高运用数学方法解决实际问题的
能力,渗透转化思想。
??? ◆情感态度
? 1.积极参与交流,并积极发表意见;
2.体验二次函数是有效描述世界的重要手段,让学生亲自体会到学习数学的价值,从而提高学生学习数学的兴趣。
【重点】?掌握从实际问题中构建二次函数模型
【难点】充分运用所学知识分析实际问题,建立函数模型,渗透数形结合思想。
【教学过程】
一、情景导入,初步认识
问题1: 欣赏下列图片,你能想到什么?
师生活动:教师提出问题,学生回答。指导学生得出抛物线在我们生活中经常遇到。
问题2:圣路易斯拱门是一座雄伟壮观的抛物线形建筑物,如果以它的顶点为原点建立坐标系,它的解析式为 ,拱顶离地面的高度为200米,求拱门的地面宽度。
师生活动:教师提出问题:
(1)怎样解决实际问题?
(2)当y=-200时,x等于多少?这个点到y轴的距离和拱门的地面宽度之间有什么关系?
学生尝试解题,教师引导学生得出解决实际问题的思路是把实际问题转化为数学问题。
设计意图:通过为学生提供解决此类问题的思路,让学生在问题解决的过程中体会二次函数与实际问题的联系。
二、类比引入,探究问题
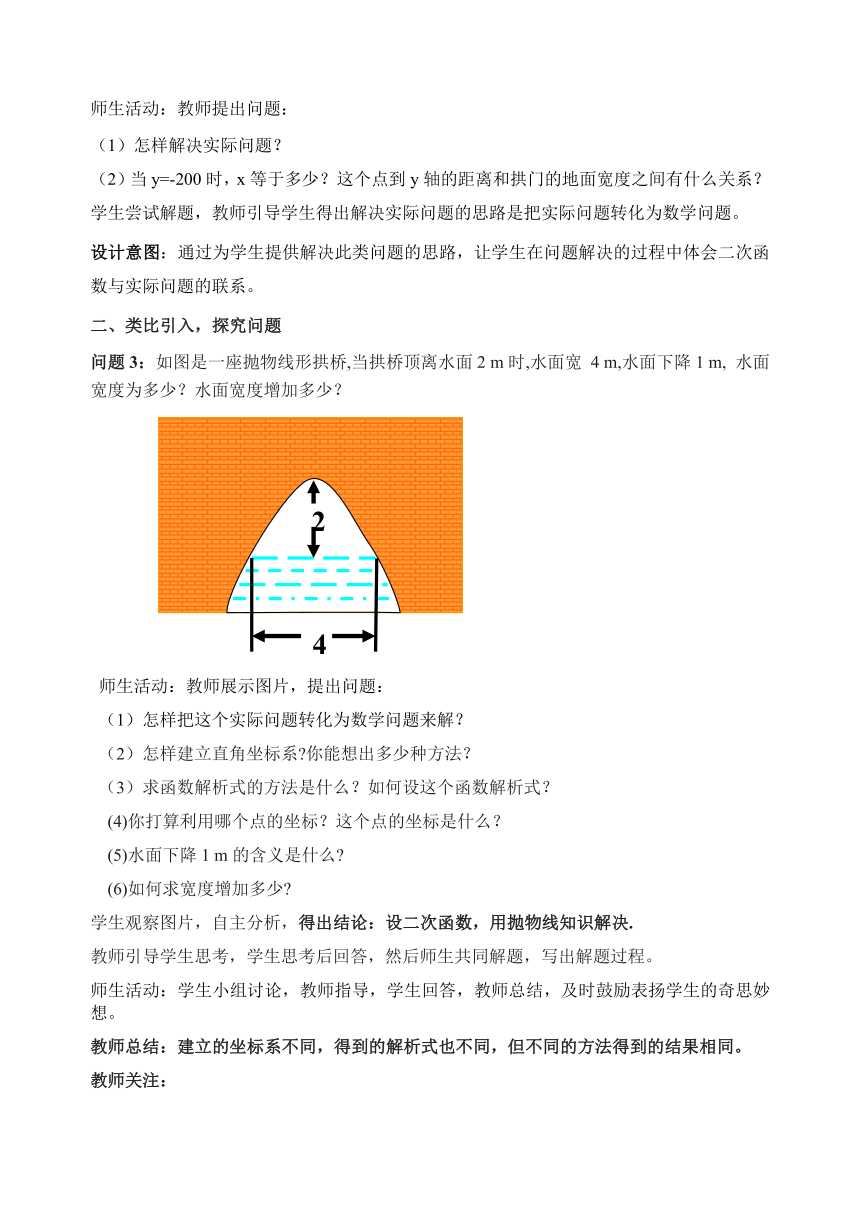
问题3:如图是一座抛物线形拱桥,当拱桥顶离水面2 m时,水面宽 4 m,水面下降1 m, 水面宽度为多少?水面宽度增加多少?
师生活动:教师展示图片,提出问题:
(1)怎样把这个实际问题转化为数学问题来解?
(2)怎样建立直角坐标系?你能想出多少种方法?
(3)求函数解析式的方法是什么?如何设这个函数解析式?
(4)你打算利用哪个点的坐标?这个点的坐标是什么?
(5)水面下降1 m的含义是什么?
(6)如何求宽度增加多少?
学生观察图片,自主分析,得出结论:设二次函数,用抛物线知识解决.
教师引导学生思考,学生思考后回答,然后师生共同解题,写出解题过程。
师生活动:学生小组讨论,教师指导,学生回答,教师总结,及时鼓励表扬学生的奇思妙想。
教师总结:建立的坐标系不同,得到的解析式也不同,但不同的方法得到的结果相同。
教师关注:
(1)学生能否用函数的观点来认识问题;
(2)学生能否建立函数模型;
(3)学生能否找到两个变量之间的关系;
(4)学生能否从拱桥问题中体会到函数模型对解决实际问题的价值.
三、归纳提升、总结步骤
问题4:通过刚才的学习,你能总结出用二次函数知识解决抛物线问题的一般步骤吗?
师生活动:学生思考回答,教师指导学生归纳,一般可分为六步:审、建、设、求、解、答。
教师总结:解此类问题的思想方法是利用数形结合思想和函数思想,合理建立直角坐标系,根据已知数据,运用待定系数法求出运动轨迹(即抛物线)的解析式,再用二次函数的性质去分析解决问题.
四、运用新知,巩固练习
1、河北省赵县的赵州桥的桥拱是抛物线型,建立如图所示的坐标系,其函数的解析式为y=-x2,当水位线在AB位置时,水面宽AB=30米,这时水面离桥拱的高度h是( )
A.5米 B. 6米 C. 8米 D.9米
2、一座抛物线型拱桥的桥拱在竖直平面内,与水平桥面相交于A、B两点,桥拱高点C到AB的距离为8m,AB=8m,D、E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为10,则DE的长为 m.
(2题)
师生活动:学生进行巩固训练,引导学生借助上面解决问题的经验解决问题。
五 、师生互动,课堂小结
通过本节课的学习你有什么收获?主要从解题思路上总结,教师指导。
师生小结:
(1)运用二次函数解决实际问题的一般步骤:
①审题,弄清已知和未知.
②将实际问题转化为数学问题,建立适当的平面直角坐标系(建立数学模型).
③结合数学模型,合理地设出二次函数解析式.
④根据题意找出点的坐标,求出抛物线解析式.
⑤利用解析式求解.
⑥得出实际问题的答案,从而解决实际问题.
(2)你对本节课有什么疑惑?说给老师或同学听听.
学生谈体会,教师进行补充、总结.
六、作业布置,课外延伸
1.某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.
(1题) (2题)
2.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以
用 表示.
(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?
(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
板书设计
22.3实际问题与二次函数(3)
————水位变化
y=-x2 y=-x2 y=-x2 y=-x2
解题步骤:审、建、设、求、解、答
【教学目标】
? ◆知识技能
??1.能够正确灵活地建立直角坐标系解决实际问题;
2.能综合利用方程、二次函数的知识解决实际问题。?
? ◆过程与方法
1. 让学生经历分析实际问题从而建立二次函数模型来解决问题的过程,体会数学建模的思想.
2.体会数学与现实生活的紧密联系,增强应用意识,提高运用数学方法解决实际问题的
能力,渗透转化思想。
??? ◆情感态度
? 1.积极参与交流,并积极发表意见;
2.体验二次函数是有效描述世界的重要手段,让学生亲自体会到学习数学的价值,从而提高学生学习数学的兴趣。
【重点】?掌握从实际问题中构建二次函数模型
【难点】充分运用所学知识分析实际问题,建立函数模型,渗透数形结合思想。
【教学过程】
一、情景导入,初步认识
问题1: 欣赏下列图片,你能想到什么?
师生活动:教师提出问题,学生回答。指导学生得出抛物线在我们生活中经常遇到。
问题2:圣路易斯拱门是一座雄伟壮观的抛物线形建筑物,如果以它的顶点为原点建立坐标系,它的解析式为 ,拱顶离地面的高度为200米,求拱门的地面宽度。
师生活动:教师提出问题:
(1)怎样解决实际问题?
(2)当y=-200时,x等于多少?这个点到y轴的距离和拱门的地面宽度之间有什么关系?
学生尝试解题,教师引导学生得出解决实际问题的思路是把实际问题转化为数学问题。
设计意图:通过为学生提供解决此类问题的思路,让学生在问题解决的过程中体会二次函数与实际问题的联系。
二、类比引入,探究问题
问题3:如图是一座抛物线形拱桥,当拱桥顶离水面2 m时,水面宽 4 m,水面下降1 m, 水面宽度为多少?水面宽度增加多少?
师生活动:教师展示图片,提出问题:
(1)怎样把这个实际问题转化为数学问题来解?
(2)怎样建立直角坐标系?你能想出多少种方法?
(3)求函数解析式的方法是什么?如何设这个函数解析式?
(4)你打算利用哪个点的坐标?这个点的坐标是什么?
(5)水面下降1 m的含义是什么?
(6)如何求宽度增加多少?
学生观察图片,自主分析,得出结论:设二次函数,用抛物线知识解决.
教师引导学生思考,学生思考后回答,然后师生共同解题,写出解题过程。
师生活动:学生小组讨论,教师指导,学生回答,教师总结,及时鼓励表扬学生的奇思妙想。
教师总结:建立的坐标系不同,得到的解析式也不同,但不同的方法得到的结果相同。
教师关注:
(1)学生能否用函数的观点来认识问题;
(2)学生能否建立函数模型;
(3)学生能否找到两个变量之间的关系;
(4)学生能否从拱桥问题中体会到函数模型对解决实际问题的价值.
三、归纳提升、总结步骤
问题4:通过刚才的学习,你能总结出用二次函数知识解决抛物线问题的一般步骤吗?
师生活动:学生思考回答,教师指导学生归纳,一般可分为六步:审、建、设、求、解、答。
教师总结:解此类问题的思想方法是利用数形结合思想和函数思想,合理建立直角坐标系,根据已知数据,运用待定系数法求出运动轨迹(即抛物线)的解析式,再用二次函数的性质去分析解决问题.
四、运用新知,巩固练习
1、河北省赵县的赵州桥的桥拱是抛物线型,建立如图所示的坐标系,其函数的解析式为y=-x2,当水位线在AB位置时,水面宽AB=30米,这时水面离桥拱的高度h是( )
A.5米 B. 6米 C. 8米 D.9米
2、一座抛物线型拱桥的桥拱在竖直平面内,与水平桥面相交于A、B两点,桥拱高点C到AB的距离为8m,AB=8m,D、E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为10,则DE的长为 m.
(2题)
师生活动:学生进行巩固训练,引导学生借助上面解决问题的经验解决问题。
五 、师生互动,课堂小结
通过本节课的学习你有什么收获?主要从解题思路上总结,教师指导。
师生小结:
(1)运用二次函数解决实际问题的一般步骤:
①审题,弄清已知和未知.
②将实际问题转化为数学问题,建立适当的平面直角坐标系(建立数学模型).
③结合数学模型,合理地设出二次函数解析式.
④根据题意找出点的坐标,求出抛物线解析式.
⑤利用解析式求解.
⑥得出实际问题的答案,从而解决实际问题.
(2)你对本节课有什么疑惑?说给老师或同学听听.
学生谈体会,教师进行补充、总结.
六、作业布置,课外延伸
1.某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.
(1题) (2题)
2.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以
用 表示.
(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?
(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
板书设计
22.3实际问题与二次函数(3)
————水位变化
y=-x2 y=-x2 y=-x2 y=-x2
解题步骤:审、建、设、求、解、答
同课章节目录
