人教版七年级数学上册1.3.1有理数的加法第一课时课件(28张PPT)
文档属性
| 名称 | 人教版七年级数学上册1.3.1有理数的加法第一课时课件(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 231.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 20:43:46 | ||
图片预览





文档简介
1.3.1 有理数的加法1
1、 比较下列各数的大小:
7和4 7和-4 -7和4 -7和-4
2、 如果向东走5米记作+5米,那么向
西走3米记作__. 3 、 已知a=-5,b=+3,
︱a ︳+ ︱b︱=__
已知a=-5,b=+3,
︱a︱ - ︱b︱=__
回顾旧知
学习目标
1、理解有理数加法计算法则
2、能熟练运用有理数加法法则进行计算
范围:自学课本16-18页思考以上部分
时间:5分钟
任务:思考下面的问题
1、小学我们学过正整数以及0的加法运算,进入中学后,我们学习了负数后,该怎样进行加法运算怎样呢?加法的计算又分几种情况?
2、总结有理数加法的计算法则。
自学探究
规定: 向东为正 向西为负
运 动 脑
小明在一条东西向的跑道上,先走了5米,又走了3米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
因为小明最后的位置与行走方向和路程有关!
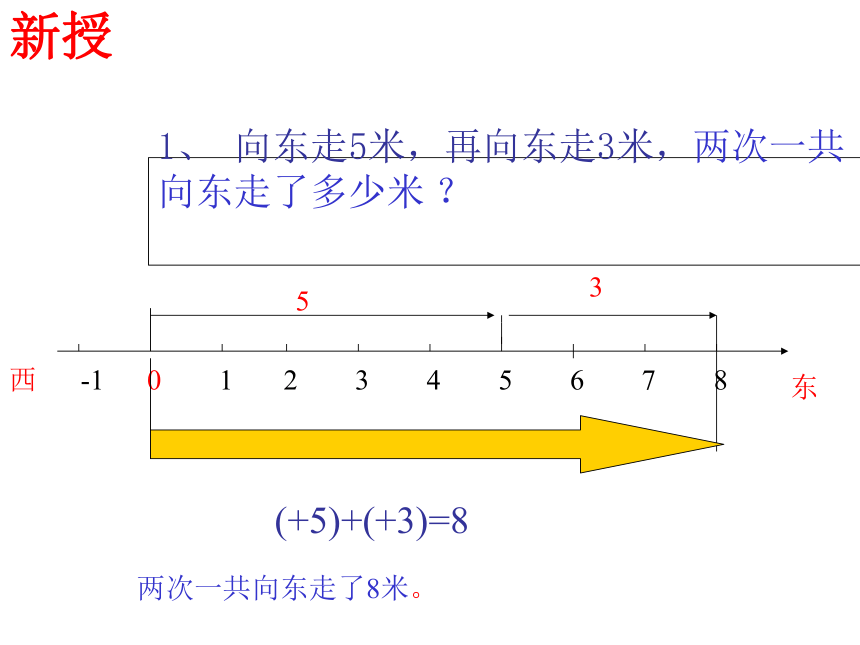
1、 向东走5米,再向东走3米,两次一共向东走了多少米 ?
-1 0 1 2 3 4 5 6 7 8
(+5)+(+3)=8
5
3
新授
东
西
两次一共向东走了8米。
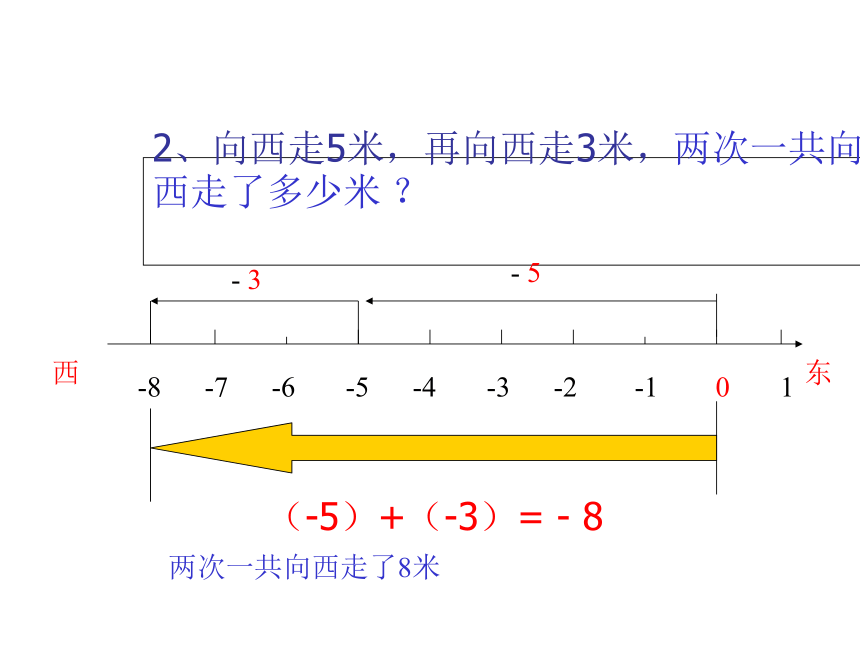
2、向西走5米,再向西走3米,两次一共向西走了多少米 ?
-8 -7 -6 -5 -4 -3 -2 -1 0 1
- 3
- 5
(-5)+(-3)= - 8
东
西
两次一共向西走了8米
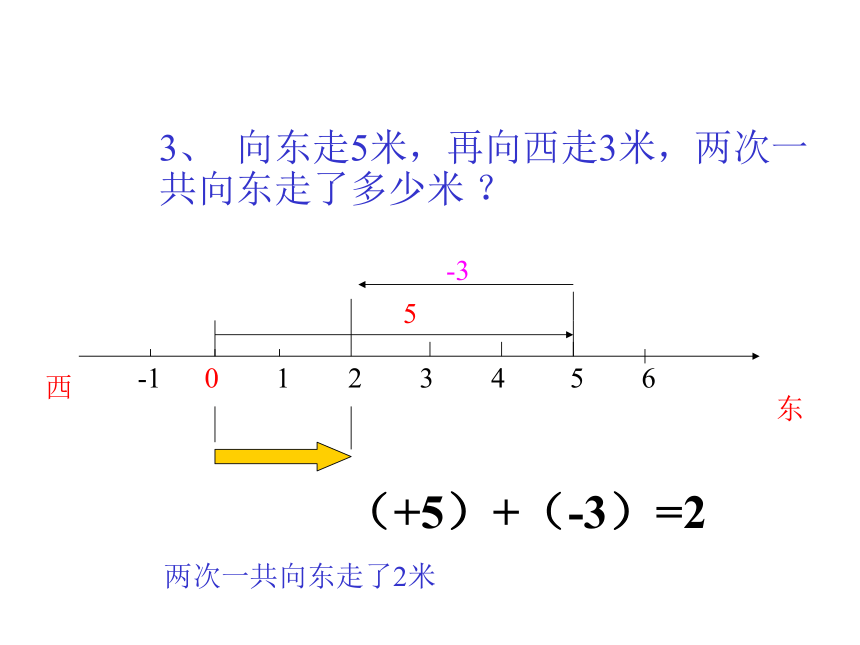
3、 向东走5米,再向西走3米,两次一共向东走了多少米 ?
(+5)+(-3)=2
-1 0 1 2 3 4 5 6
5
-3
东
西
两次一共向东走了2米
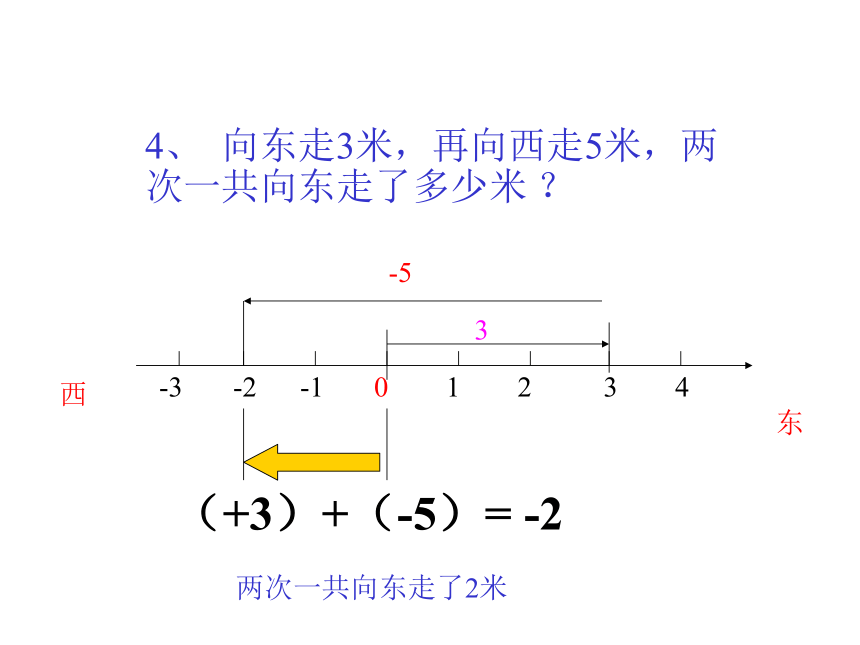
4、 向东走3米,再向西走5米,两 次一共向东走了多少米 ?
(+3)+(-5)= -2
-3 -2 -1 0 1 2 3 4
3
-5
东
西
两次一共向东走了2米
5、 向东走5米,再向西走5米,两次一共 向东走了多少米?
5+(-5)=0
-1 0 1 2 3 4 5 6
- 5
5
东
西
6、 向东走5米,再向西走0米, 两次一共向东走了多少米?
(+5)+0= + 5
0 1 2 3 4 5 6
+5
东
西
7、 向西走5米,再向东走0米, 两次一共向东走了多少米?
(-5)+0= - 5
-5 -4 -3 -2 -1 0 1
-5
东
西
(+ 5) + (+ 3) = + 8
( - 5 ) + ( - 3 ) = - 8
5 +(-3) = + 2
3 +(-5) = - 2
5 +(-5) = 0
+5 + 0 = +5
(- 5)+ 0 = - 5
同号两数相加
异号两数相加
一数与零相加
想一想:你能从这些例子中发现什么吗?
* 你能试着总结出有理数的加法的运算规律吗?
两个相反数相加
( - 7 ) + ( -6 ) = - 13
( - 8 ) + ( -6 ) = - 14
(+5) + ( + 15) = +20
(+9) + (+ 3) = + 12
从得数中你能发现它的符号有什么规律?
( - 7 ) + (- 6 ) = - 13
( - 8 ) + (- 6 ) = - 14
(+ 5) + (+ 15) = + 20
(+9) + (+ 3) = + 12
符号确定后 得数怎么算呢?
从得数中你能发现它的符号有什么规律吗?
取与加数相同的符号
将各个加数的绝对值相加
(+ 5) + ( -3 ) = + 2
(+3) + ( -5 ) = - 2
( +5) + (- 9 ) = - 4
(- 11) + (+4 ) = - 7
从得数中你能发现它的符号有规律吗?
取绝对值大的符号
符号确定后 得数怎么算呢?
将加数的绝对值 大的减去小的作为差的绝对值
有理数加法计算方法总结
有理数加法运算三步走:
一 看:看符合加法法则那一条;
二 定:定和的符号是正还是负;
三计算:利用绝对值相加或相减算出结果。
分析特征 强化理解 总结步骤
( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓ ↓
同号两数相加 取相同符号 两个加数的绝对值
相加
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓ ↓
异号两数相加 取绝对值较大 两个加数的绝对值
的符号 由大的减去小的
(1)(-3)+(-9)(2) (-1/2)+(+1/3)
例: 计算
解:(-1/2)+(+1/3)
=-( )
解: (-3)+ (-9)
=-( )
3+9
=-12
1/2-1/3
=-(3/6-2/6)
=- 1/6
有理数加法法则:
1)同号两数相加,取相同的符号,并把绝对值相加。
2)异号两数相加,取绝对值
较大的符号,并用较大的
绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3)一个数同0相加,仍得这个数。
有理数加法法则口诀:
同号相加一边倒;(同号数相加,取相同符号并把绝对值相加)
异号相加大减小,(异号数相加,用绝对值大的减去绝对值小的数)
符号跟着大的跑;(符号跟绝对值大的相同)
绝对值相加0正好。(互为相反数的两个数相加和为0)
练习一:
(1)15 +(-22) =
(2)(-13)+(-8)=
(3)(-0·9)+ 1·5 =
(4)2·7 + (-3·5) =
(5)1/2 +(-2/3) =
(6)(-1/4)+(-1/3)=
自学检测
课本第18页 练习
第1题 第2题
班级交流
(1) 一个皮球,上升了10米,又上升的-3米,则共上升了 米
(2) 一个数是11,另一个数比11的相反数大2,那么这两个数的和为 。
课堂小结:
1、掌握有理数的加法法则,正确地进
行加法运算。
2、两个有理数相加,首先判断加法类
型,再确定符号,最后确定绝
对值是和还是差。
有理数加法法则:
1)同号两数相加,取相同的符号,并把绝对值相加。
2)异号两数相加,取绝对值较大的符号,
并用较大的 绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3)一个数同0相加,仍得这个数。
达标检测
课本P19 练习3
作业本完成
谢谢您的合作
再见
1、 比较下列各数的大小:
7和4 7和-4 -7和4 -7和-4
2、 如果向东走5米记作+5米,那么向
西走3米记作__. 3 、 已知a=-5,b=+3,
︱a ︳+ ︱b︱=__
已知a=-5,b=+3,
︱a︱ - ︱b︱=__
回顾旧知
学习目标
1、理解有理数加法计算法则
2、能熟练运用有理数加法法则进行计算
范围:自学课本16-18页思考以上部分
时间:5分钟
任务:思考下面的问题
1、小学我们学过正整数以及0的加法运算,进入中学后,我们学习了负数后,该怎样进行加法运算怎样呢?加法的计算又分几种情况?
2、总结有理数加法的计算法则。
自学探究
规定: 向东为正 向西为负
运 动 脑
小明在一条东西向的跑道上,先走了5米,又走了3米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
因为小明最后的位置与行走方向和路程有关!
1、 向东走5米,再向东走3米,两次一共向东走了多少米 ?
-1 0 1 2 3 4 5 6 7 8
(+5)+(+3)=8
5
3
新授
东
西
两次一共向东走了8米。
2、向西走5米,再向西走3米,两次一共向西走了多少米 ?
-8 -7 -6 -5 -4 -3 -2 -1 0 1
- 3
- 5
(-5)+(-3)= - 8
东
西
两次一共向西走了8米
3、 向东走5米,再向西走3米,两次一共向东走了多少米 ?
(+5)+(-3)=2
-1 0 1 2 3 4 5 6
5
-3
东
西
两次一共向东走了2米
4、 向东走3米,再向西走5米,两 次一共向东走了多少米 ?
(+3)+(-5)= -2
-3 -2 -1 0 1 2 3 4
3
-5
东
西
两次一共向东走了2米
5、 向东走5米,再向西走5米,两次一共 向东走了多少米?
5+(-5)=0
-1 0 1 2 3 4 5 6
- 5
5
东
西
6、 向东走5米,再向西走0米, 两次一共向东走了多少米?
(+5)+0= + 5
0 1 2 3 4 5 6
+5
东
西
7、 向西走5米,再向东走0米, 两次一共向东走了多少米?
(-5)+0= - 5
-5 -4 -3 -2 -1 0 1
-5
东
西
(+ 5) + (+ 3) = + 8
( - 5 ) + ( - 3 ) = - 8
5 +(-3) = + 2
3 +(-5) = - 2
5 +(-5) = 0
+5 + 0 = +5
(- 5)+ 0 = - 5
同号两数相加
异号两数相加
一数与零相加
想一想:你能从这些例子中发现什么吗?
* 你能试着总结出有理数的加法的运算规律吗?
两个相反数相加
( - 7 ) + ( -6 ) = - 13
( - 8 ) + ( -6 ) = - 14
(+5) + ( + 15) = +20
(+9) + (+ 3) = + 12
从得数中你能发现它的符号有什么规律?
( - 7 ) + (- 6 ) = - 13
( - 8 ) + (- 6 ) = - 14
(+ 5) + (+ 15) = + 20
(+9) + (+ 3) = + 12
符号确定后 得数怎么算呢?
从得数中你能发现它的符号有什么规律吗?
取与加数相同的符号
将各个加数的绝对值相加
(+ 5) + ( -3 ) = + 2
(+3) + ( -5 ) = - 2
( +5) + (- 9 ) = - 4
(- 11) + (+4 ) = - 7
从得数中你能发现它的符号有规律吗?
取绝对值大的符号
符号确定后 得数怎么算呢?
将加数的绝对值 大的减去小的作为差的绝对值
有理数加法计算方法总结
有理数加法运算三步走:
一 看:看符合加法法则那一条;
二 定:定和的符号是正还是负;
三计算:利用绝对值相加或相减算出结果。
分析特征 强化理解 总结步骤
( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓ ↓
同号两数相加 取相同符号 两个加数的绝对值
相加
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓ ↓
异号两数相加 取绝对值较大 两个加数的绝对值
的符号 由大的减去小的
(1)(-3)+(-9)(2) (-1/2)+(+1/3)
例: 计算
解:(-1/2)+(+1/3)
=-( )
解: (-3)+ (-9)
=-( )
3+9
=-12
1/2-1/3
=-(3/6-2/6)
=- 1/6
有理数加法法则:
1)同号两数相加,取相同的符号,并把绝对值相加。
2)异号两数相加,取绝对值
较大的符号,并用较大的
绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3)一个数同0相加,仍得这个数。
有理数加法法则口诀:
同号相加一边倒;(同号数相加,取相同符号并把绝对值相加)
异号相加大减小,(异号数相加,用绝对值大的减去绝对值小的数)
符号跟着大的跑;(符号跟绝对值大的相同)
绝对值相加0正好。(互为相反数的两个数相加和为0)
练习一:
(1)15 +(-22) =
(2)(-13)+(-8)=
(3)(-0·9)+ 1·5 =
(4)2·7 + (-3·5) =
(5)1/2 +(-2/3) =
(6)(-1/4)+(-1/3)=
自学检测
课本第18页 练习
第1题 第2题
班级交流
(1) 一个皮球,上升了10米,又上升的-3米,则共上升了 米
(2) 一个数是11,另一个数比11的相反数大2,那么这两个数的和为 。
课堂小结:
1、掌握有理数的加法法则,正确地进
行加法运算。
2、两个有理数相加,首先判断加法类
型,再确定符号,最后确定绝
对值是和还是差。
有理数加法法则:
1)同号两数相加,取相同的符号,并把绝对值相加。
2)异号两数相加,取绝对值较大的符号,
并用较大的 绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
3)一个数同0相加,仍得这个数。
达标检测
课本P19 练习3
作业本完成
谢谢您的合作
再见
