人教版数学八年级上册12.2 三角形全等的判定课件( 第2课时 共16张PPT)
文档属性
| 名称 | 人教版数学八年级上册12.2 三角形全等的判定课件( 第2课时 共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 14:54:08 | ||
图片预览


文档简介
三角形全等的判定
第2课时
1、什么是全等三角形?
能够完全重合的两个三角形。
一、复习旧知
2、全等三角形有哪些性质?
三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)。
3、全等三角形的判定方法之一
对应边相等,对应角相等。
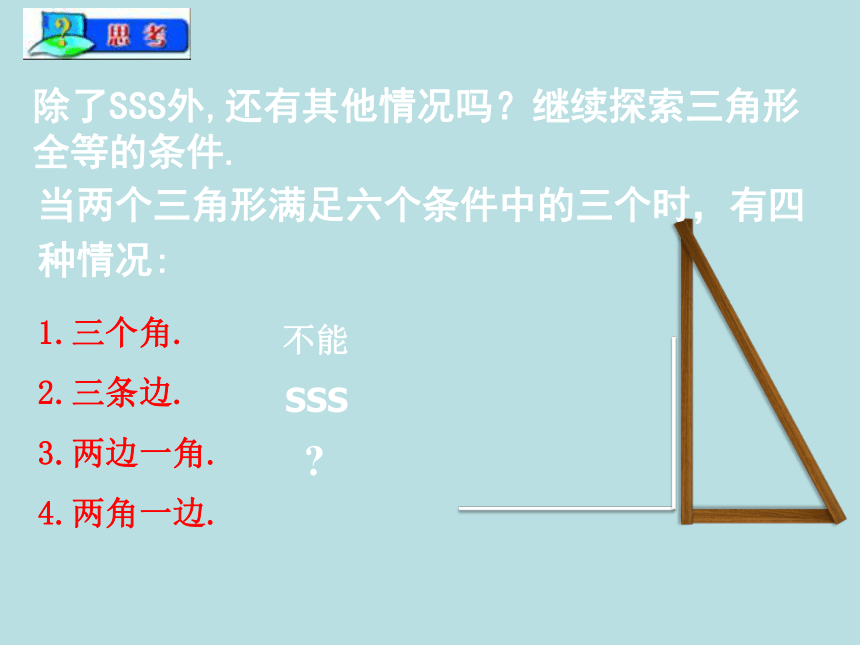
除了SSS外,还有其他情况吗?继续探索三角形全等的条件.
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能
?
1.三个角.
2.三条边.
3.两边一角.
4.两角一边.
A
B
C
A′
D
E
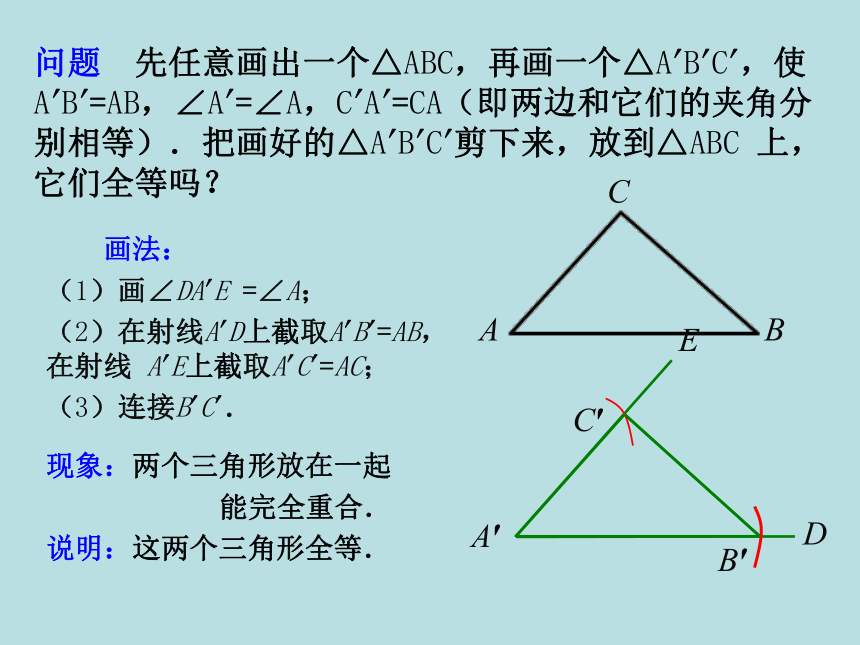
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1)画∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,在射线 A′E上截取A′C′=AC;
(3)连接B′C′.
B′
C′
问题 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,C′A′=CA(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?
几何语言:
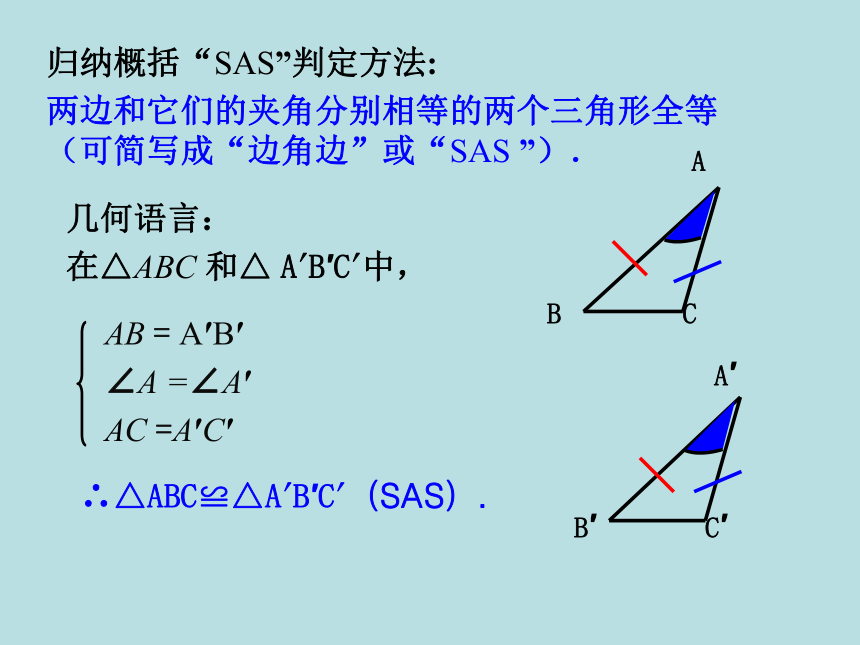
在△ABC 和△ A′B′C′中,
归纳概括“SAS”判定方法:
两边和它们的夹角分别相等的两个三角形全等(可简写成“边角边”或“SAS ”).
AB = A′B′
∠A =∠A′
AC =A′C′
∴△ABC≌△A′B′C′(SAS).
A
B
C
A′
B′
C′
A
B
D
E
C
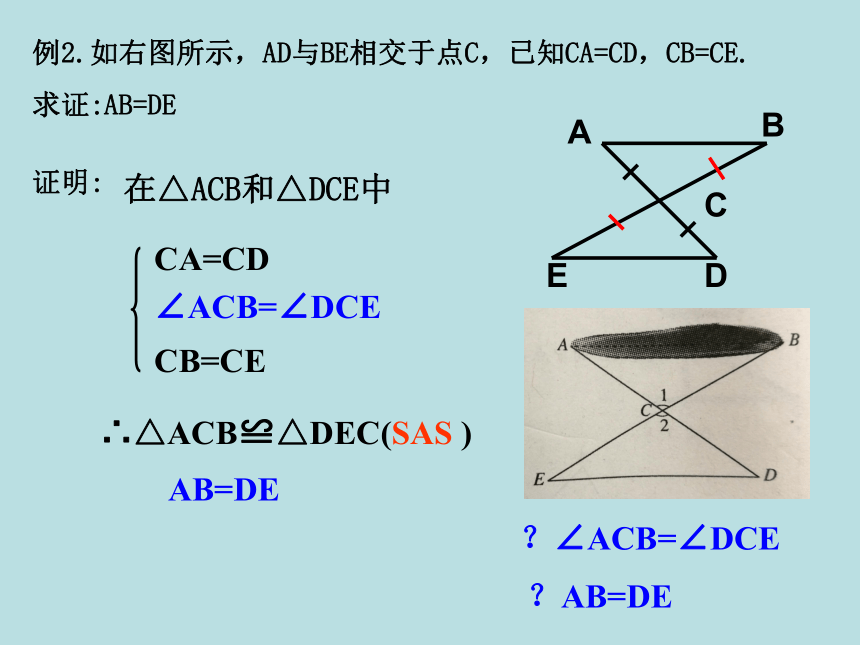
例2.如右图所示,AD与BE相交于点C,已知CA=CD,CB=CE.
求证:AB=DE
证明:
在△ACB和△DCE中
CA=CD
CB=CE
∠ACB=∠DCE
∴△ACB≌△DEC(SAS )
?∠ACB=∠DCE
?AB=DE
AB=DE
因为全等三角形的对应边相等,对应角相等,所以证明线段相等或者角相等,常常通过证明它们是全等三角形的对应边或对应角来解决。
总结:
如图,把一长一短的两根木棍的一端固定在一起,摆出?ABC,固定住长木棍,转动短木棍,得到?ABD,这个实验说明了什么?
这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等。
1.下列图形中有没有全等三角形,并说明全等的理由.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
图甲与图丙全等,依据就是“SAS”,而图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等.
试一试
如右图所示,AB=AC,AD=AE。求证:△ABE≌△ACD。
练一练
练习题:如右图,AC=DC,BC=EC,∠ACD=∠BCE,
求证:∠A=∠D。
类型之一 利用“SAS”证明三角形全等
证明:因为∠ACD=∠BCE,
所以∠ACD+∠ACE=∠BCE+∠ACE,
即∠DCE=∠ACB
在△ACB和△DCE中,AC=DC,∠ACB=∠DCE,BC=EC,
所以 △ACB≌△DCE(SAS )
所以 ∠A=∠D
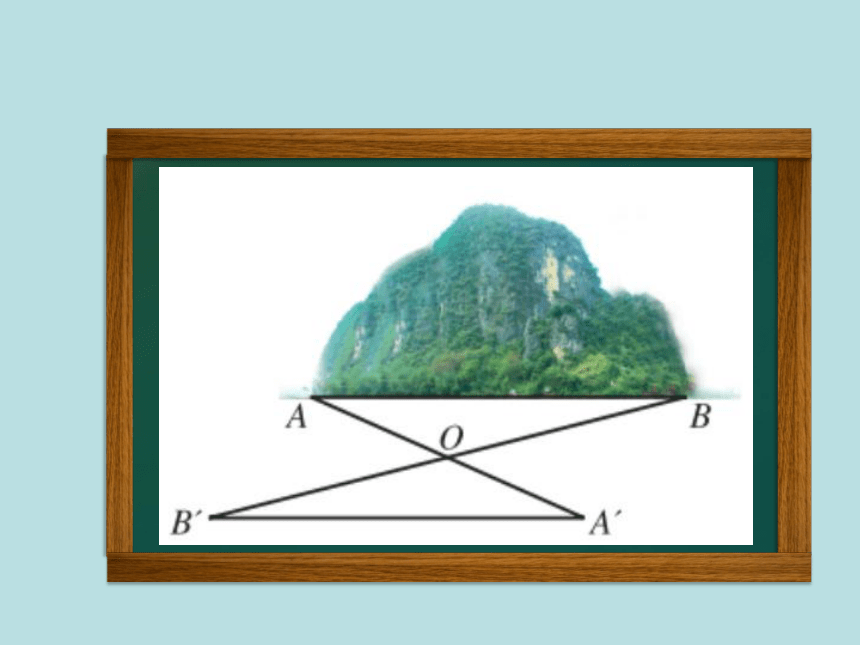
挑战题: 如右图,OA=OD,AC=DB,图中有哪些三角形全等?为什么?
类型之二 灵活运用三角形全等的判定方法证明三角全等
解:△OAB≌△ODC
△ABC≌△DCB
理由如下: 因为OA=OD,AC=DB
所以 AC-OA=DB-OD,即OC=OB
又因为∠AOB=∠DOC
所以 △OAB≌△ODC(SAS )
所以 AB=DC
又因为BC=CB,AC=DB
所以 △ABC≌△DCB(SSS )
1、用SAS的方法来确定两个三角形全等;
本堂小结
2、用SAS的方法要注意两边夹一角,若是SSA不能证明两个三角形全等。
全效学习第24页至27页。
作业布置
谢
谢
指
导
第2课时
1、什么是全等三角形?
能够完全重合的两个三角形。
一、复习旧知
2、全等三角形有哪些性质?
三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)。
3、全等三角形的判定方法之一
对应边相等,对应角相等。
除了SSS外,还有其他情况吗?继续探索三角形全等的条件.
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能
?
1.三个角.
2.三条边.
3.两边一角.
4.两角一边.
A
B
C
A′
D
E
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1)画∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,在射线 A′E上截取A′C′=AC;
(3)连接B′C′.
B′
C′
问题 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,C′A′=CA(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?
几何语言:
在△ABC 和△ A′B′C′中,
归纳概括“SAS”判定方法:
两边和它们的夹角分别相等的两个三角形全等(可简写成“边角边”或“SAS ”).
AB = A′B′
∠A =∠A′
AC =A′C′
∴△ABC≌△A′B′C′(SAS).
A
B
C
A′
B′
C′
A
B
D
E
C
例2.如右图所示,AD与BE相交于点C,已知CA=CD,CB=CE.
求证:AB=DE
证明:
在△ACB和△DCE中
CA=CD
CB=CE
∠ACB=∠DCE
∴△ACB≌△DEC(SAS )
?∠ACB=∠DCE
?AB=DE
AB=DE
因为全等三角形的对应边相等,对应角相等,所以证明线段相等或者角相等,常常通过证明它们是全等三角形的对应边或对应角来解决。
总结:
如图,把一长一短的两根木棍的一端固定在一起,摆出?ABC,固定住长木棍,转动短木棍,得到?ABD,这个实验说明了什么?
这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等。
1.下列图形中有没有全等三角形,并说明全等的理由.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
图甲与图丙全等,依据就是“SAS”,而图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等.
试一试
如右图所示,AB=AC,AD=AE。求证:△ABE≌△ACD。
练一练
练习题:如右图,AC=DC,BC=EC,∠ACD=∠BCE,
求证:∠A=∠D。
类型之一 利用“SAS”证明三角形全等
证明:因为∠ACD=∠BCE,
所以∠ACD+∠ACE=∠BCE+∠ACE,
即∠DCE=∠ACB
在△ACB和△DCE中,AC=DC,∠ACB=∠DCE,BC=EC,
所以 △ACB≌△DCE(SAS )
所以 ∠A=∠D
挑战题: 如右图,OA=OD,AC=DB,图中有哪些三角形全等?为什么?
类型之二 灵活运用三角形全等的判定方法证明三角全等
解:△OAB≌△ODC
△ABC≌△DCB
理由如下: 因为OA=OD,AC=DB
所以 AC-OA=DB-OD,即OC=OB
又因为∠AOB=∠DOC
所以 △OAB≌△ODC(SAS )
所以 AB=DC
又因为BC=CB,AC=DB
所以 △ABC≌△DCB(SSS )
1、用SAS的方法来确定两个三角形全等;
本堂小结
2、用SAS的方法要注意两边夹一角,若是SSA不能证明两个三角形全等。
全效学习第24页至27页。
作业布置
谢
谢
指
导
