人教版小学数学六年级上册讲义 圆的周长和面积
文档属性
| 名称 | 人教版小学数学六年级上册讲义 圆的周长和面积 |  | |
| 格式 | docx | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 07:22:51 | ||
图片预览



文档简介
第六讲 圆的周长和面积
课程目标
掌握圆的周长与面积的计算公式。
能运用直接法或间接法求组合图形的周长或面积。
课程重点
能运用直接法或间接法求组合图形的周长或面积。
课程难点
解决圆中方、方中圆问题。
教学方法建议
注意先练后讲,体现针对性。
一、知识梳理
圆的认识:圆中心的一点叫做圆心,圆心一般用字母“o”表示;连接圆心和圆上任意一点的线段叫做半径,半径一般用字母“r”表示;通过圆心并且两端都在圆上的线段叫做直径,直径一般用字母“d”表示。
d
O
r
圆心决定圆的位置, 半径决定圆的大小。
圆周率:圆的周长和直径的比值,用字母? 表示。( ? ≈3.14)
圆的面积:圆所占平面的大小叫圆的面积,圆的面积一般用字母“S”表示, S =πr?. 圆环的面积计算公式:S =πR?-πr?=π(R?-r?)
扇形的面积公式: S ? ?r 2 ?
n
360
二、方法归纳
设数法:当题目中半径未知时,求两个圆周长或面积的比可用设数法。
整体法(整体思想):在解决圆中方问题时,圆的直径即是正方形对角线,这时求出半径的平方当作一个整体。
三、课堂精讲
例 1. 填表
圆的半径(cm)
直径(cm)
面积(cm2)
周长(cm)
12
8
78.5
3.14
【规律方法】理解公式的推倒过程,直接套公式进行计算。
【搭配课堂训练题】
【难度分级】 A
求下面各圆的面积。
(1)d = 10dm (2)C = 18.84m
一个圆和一个正方形的周长都是 25.12 厘米,它们的面积( ) A.正方形大 B.圆大 C.一样大
3.(中大附中)圆的半径从 8cm 减少到 6cm,圆的面积减少了( )
A. 4 ? 平方厘米 B.28 平方厘米 C.28 ? 平方厘米
4.一只挂钟的分针长 80mm,分针的针尖 1 小时走( )毫米。
5.( 玉岩天健)一个圆环,外圆直径是 10cm,内圆直径是 6cm,这个圆环的面积是
( )。
6.( 白云广雅)自行车车轮向前滚动两周走过的距离是 a 米,车轮的周长是( ) 米,直径是( )米。
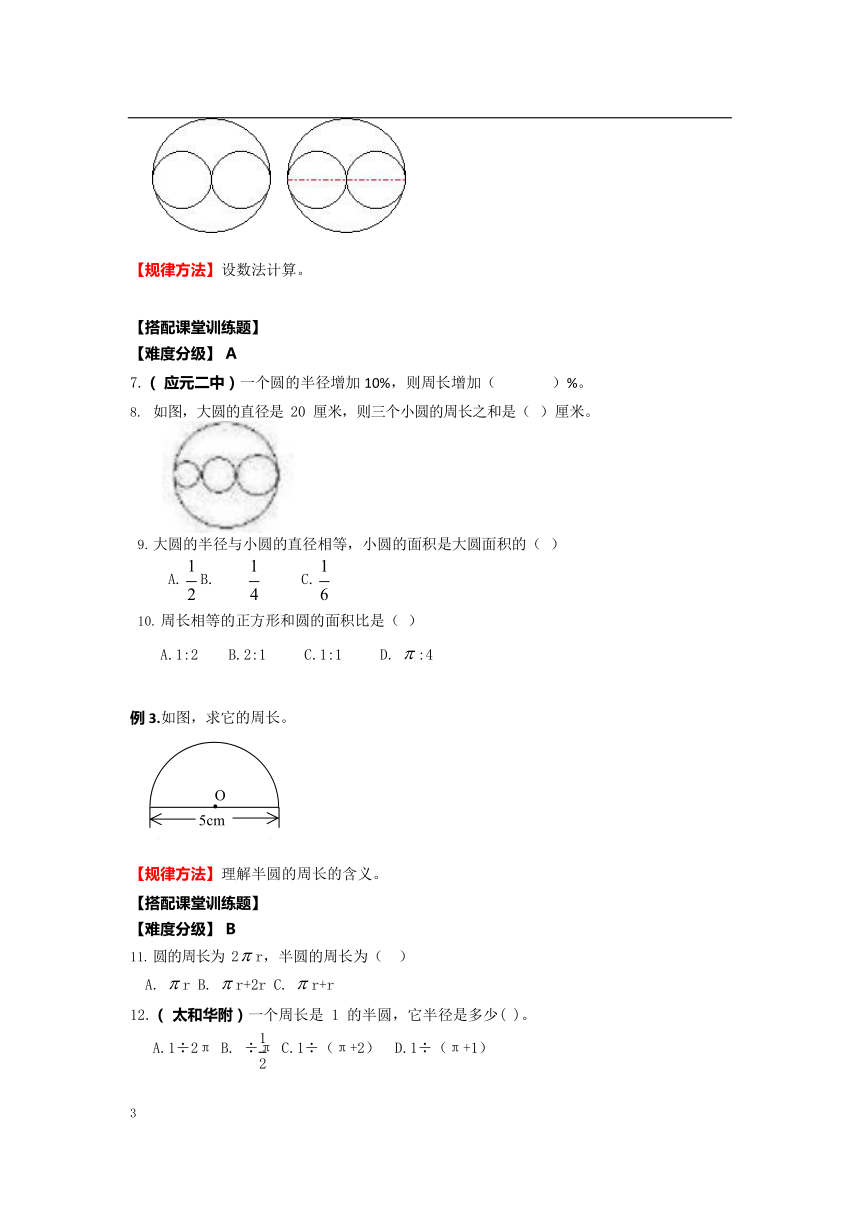
例 2.小乌龟和小白兔又要比赛了,这一次小白兔沿大圆跑一圈,小乌龟沿两个小圆“∞”跑一圈,谁跑的路程长呢?好好想一想。
【规律方法】设数法计算。
【搭配课堂训练题】
【难度分级】 A
7.( 应元二中)一个圆的半径增加 10%,则周长增加( )%。
如图,大圆的直径是 20 厘米,则三个小圆的周长之和是( )厘米。
大圆的半径与小圆的直径相等,小圆的面积是大圆面积的( )
1 1
A. B.
2 4
1
C.
6
周长相等的正方形和圆的面积比是( )
O
5cm
A.1:2 B.2:1 C.1:1 D. ? :4 例 3.如图,求它的周长。
【规律方法】理解半圆的周长的含义。
【搭配课堂训练题】
【难度分级】 B
圆的周长为 2 ? r,半圆的周长为( )
A. ? r B. ? r+2r C. ? r+r
12.( 太和华附)一个周长是 1 的半圆,它半径是多少( )。
1
A.1÷2π B. ÷π C.1÷(π+2) D.1÷(π+1)
2
例 4.(1)在一个正方形里画一个最大的圆,圆的面积是正方形面积的( )。
A. 1 B. 3 C. ? D. ?
2 4 4
(2)(中大附中)小方桌面的边长是 1 米,把它的四边撑开,就成了一张圆桌面
(如右图)。圆桌面的面积是( )平方米。
【规律方法】外圆里方及外方里圆。
【搭配课堂训练题】
【难度分级】 B
13.在一张长 12 厘米,宽 8 厘米的长方形纸中剪一个最大的圆,这个圆的面积是( )平
方厘米。
14.( 白云广雅)如图,图的直径 d=10cm ( ? 取 3.14). 则阴影部分的面积是 ( )
cm2
15.一张边长为 a 米的正方形纸,如果在这张纸上剪四个相等且最大的圆,那么这张纸的利用率是( )
A.78.5% B.75% C.82% D.80%
1482090323850例 5.求阴影部分的面积(长度单位:厘米)
【规律方法】弓形面积等于扇形减三角形面积。
【搭配课堂训练题】
【难度分级】 B
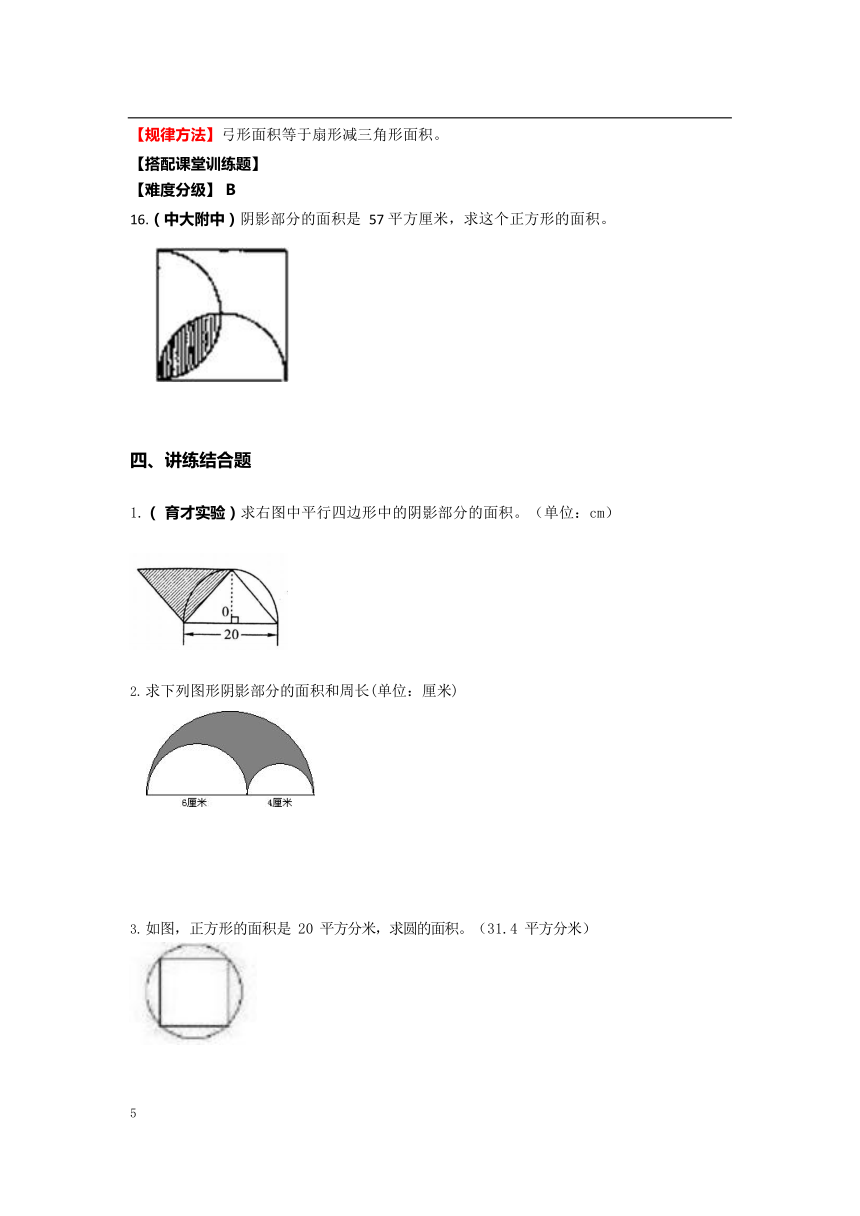
16.(中大附中)阴影部分的面积是 57 平方厘米,求这个正方形的面积。
1365250143510
四、讲练结合题
1.( 育才实验)求右图中平行四边形中的阴影部分的面积。(单位:cm)
1143000252730
求下列图形阴影部分的面积和周长(单位:厘米)
128778094615
1143000238760如图,正方形的面积是 20 平方分米,求圆的面积。(31.4 平方分米)
如图所示,求图中阴影部分的面积(单位:厘米)。(16.82 平方厘米)
1275715178435
C
B
A
三角形 ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小 28 平方厘米. AB 长 40 厘米, BC 长是多少厘米?(32.8 厘米)
6.(省实天河)一个正方形的草地,边长是 3 米,在两个对角的顶点处各种一棵树, 树上各栓一只羊,绳长都是 3 米,问两只羊都能吃到草地的面积有多大?
五.课后自测练习
一座石英钟,时针长 2 分米,一昼夜针尖走了多少分米?
一个自行车轮胎的外直径是 70cm,如果每分钟车轮转 200 周,一小时能行多少千米?
(得数保留整数)
一个圆形花坛的直径是 20 米,现在要在花坛的周围铺一条 2 米宽的石板路,这条石板路的占地面积是多少平方米?
1209675521335有七根直径 5 厘米的塑料管,用一根橡皮筋把它们勒紧一捆(如左下图),此时橡皮筋的长度是多少厘米?
5.( 广大附中)下图半圆中,AB 为直径,C 为弧 AB 的中点,求阴影部分面积之和。(单位:厘米)
13423906527806.(天河省实)如图,用一块面积为 36 平方厘米的圆形铝板下料,从中裁出了 7 个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?
7.右图中 4 个圆的圆心是正方形的 4 个顶点,它们的公共点是该正方形的中心.如果每个圆
的半径都是 1 厘米,那么阴影部分的总面积是多少平方厘米?
第六讲 圆的周长和面积【答案】
课堂精讲
例 1. 填表
圆的半径(cm)
直径(cm)
面积( cm2 )
周长(cm)
12
24
452.16
75.36
4
8
50.24
25.12
12.5
25
490.625
78.5
例 2.设小圆的直径为 1 米,则大圆的周长为 3.14×2=6.28(米)
小圆的周长为 3.14×1×2=6.28(米)
【搭配课堂训练题】
7.周长增加( 10 )%。
8.三个小圆的周长之和是( 62.8 )厘米。
9. B 10.D
例 3. 周长为 3.14×5÷2+5=12.85(cm)
【搭配课堂训练题】 11.B 12.C
例 4.(1)C (2)圆桌面的面积是( 1.57 )平方米。
【搭配课堂训练题】
13.这个圆的面积是( 50.24 )平方厘米。 14.阴影部分的面积是 ( 37.5 ) cm2
15.A
1
例 5.解:两个弓形面积为 ?( 3)2 - 1 ? 3? 3 ? 9 ? - 9 ? 1.2825(平方厘米)
2 2 2
【搭配课堂训练题】
2 8 4
16.解:这个正方形的面积为 400 平方厘米。
讲练结合题
答:阴影部分的面积为 100 平方厘米。
答:阴影部分的面积为 18.84 平方厘米,周长为 62.8 厘米。
答:圆的面积为 31.4 平方分米。
答:图中阴影部分的面积为 16.82 平方厘米。
答:BC 长是 32.8 厘米。
答:两只羊都能吃到草地的面积 5.13 平方米。
课后自测练习
答:一昼夜针尖走了 25.12 分米.
答:一小时能行 26 千米.
答:这条石板路的占地面积是 138.16 平方米.
答:此时橡皮筋的长度是 45.7 厘米。
答:阴影部分面积之和为 63.585 平方厘米。
答:所余下的边角料的总面积是 8 平方厘米。
答:阴影部分的总面积是 10.28 平方厘米。
课程目标
掌握圆的周长与面积的计算公式。
能运用直接法或间接法求组合图形的周长或面积。
课程重点
能运用直接法或间接法求组合图形的周长或面积。
课程难点
解决圆中方、方中圆问题。
教学方法建议
注意先练后讲,体现针对性。
一、知识梳理
圆的认识:圆中心的一点叫做圆心,圆心一般用字母“o”表示;连接圆心和圆上任意一点的线段叫做半径,半径一般用字母“r”表示;通过圆心并且两端都在圆上的线段叫做直径,直径一般用字母“d”表示。
d
O
r
圆心决定圆的位置, 半径决定圆的大小。
圆周率:圆的周长和直径的比值,用字母? 表示。( ? ≈3.14)
圆的面积:圆所占平面的大小叫圆的面积,圆的面积一般用字母“S”表示, S =πr?. 圆环的面积计算公式:S =πR?-πr?=π(R?-r?)
扇形的面积公式: S ? ?r 2 ?
n
360
二、方法归纳
设数法:当题目中半径未知时,求两个圆周长或面积的比可用设数法。
整体法(整体思想):在解决圆中方问题时,圆的直径即是正方形对角线,这时求出半径的平方当作一个整体。
三、课堂精讲
例 1. 填表
圆的半径(cm)
直径(cm)
面积(cm2)
周长(cm)
12
8
78.5
3.14
【规律方法】理解公式的推倒过程,直接套公式进行计算。
【搭配课堂训练题】
【难度分级】 A
求下面各圆的面积。
(1)d = 10dm (2)C = 18.84m
一个圆和一个正方形的周长都是 25.12 厘米,它们的面积( ) A.正方形大 B.圆大 C.一样大
3.(中大附中)圆的半径从 8cm 减少到 6cm,圆的面积减少了( )
A. 4 ? 平方厘米 B.28 平方厘米 C.28 ? 平方厘米
4.一只挂钟的分针长 80mm,分针的针尖 1 小时走( )毫米。
5.( 玉岩天健)一个圆环,外圆直径是 10cm,内圆直径是 6cm,这个圆环的面积是
( )。
6.( 白云广雅)自行车车轮向前滚动两周走过的距离是 a 米,车轮的周长是( ) 米,直径是( )米。
例 2.小乌龟和小白兔又要比赛了,这一次小白兔沿大圆跑一圈,小乌龟沿两个小圆“∞”跑一圈,谁跑的路程长呢?好好想一想。
【规律方法】设数法计算。
【搭配课堂训练题】
【难度分级】 A
7.( 应元二中)一个圆的半径增加 10%,则周长增加( )%。
如图,大圆的直径是 20 厘米,则三个小圆的周长之和是( )厘米。
大圆的半径与小圆的直径相等,小圆的面积是大圆面积的( )
1 1
A. B.
2 4
1
C.
6
周长相等的正方形和圆的面积比是( )
O
5cm
A.1:2 B.2:1 C.1:1 D. ? :4 例 3.如图,求它的周长。
【规律方法】理解半圆的周长的含义。
【搭配课堂训练题】
【难度分级】 B
圆的周长为 2 ? r,半圆的周长为( )
A. ? r B. ? r+2r C. ? r+r
12.( 太和华附)一个周长是 1 的半圆,它半径是多少( )。
1
A.1÷2π B. ÷π C.1÷(π+2) D.1÷(π+1)
2
例 4.(1)在一个正方形里画一个最大的圆,圆的面积是正方形面积的( )。
A. 1 B. 3 C. ? D. ?
2 4 4
(2)(中大附中)小方桌面的边长是 1 米,把它的四边撑开,就成了一张圆桌面
(如右图)。圆桌面的面积是( )平方米。
【规律方法】外圆里方及外方里圆。
【搭配课堂训练题】
【难度分级】 B
13.在一张长 12 厘米,宽 8 厘米的长方形纸中剪一个最大的圆,这个圆的面积是( )平
方厘米。
14.( 白云广雅)如图,图的直径 d=10cm ( ? 取 3.14). 则阴影部分的面积是 ( )
cm2
15.一张边长为 a 米的正方形纸,如果在这张纸上剪四个相等且最大的圆,那么这张纸的利用率是( )
A.78.5% B.75% C.82% D.80%
1482090323850例 5.求阴影部分的面积(长度单位:厘米)
【规律方法】弓形面积等于扇形减三角形面积。
【搭配课堂训练题】
【难度分级】 B
16.(中大附中)阴影部分的面积是 57 平方厘米,求这个正方形的面积。
1365250143510
四、讲练结合题
1.( 育才实验)求右图中平行四边形中的阴影部分的面积。(单位:cm)
1143000252730
求下列图形阴影部分的面积和周长(单位:厘米)
128778094615
1143000238760如图,正方形的面积是 20 平方分米,求圆的面积。(31.4 平方分米)
如图所示,求图中阴影部分的面积(单位:厘米)。(16.82 平方厘米)
1275715178435
C
B
A
三角形 ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小 28 平方厘米. AB 长 40 厘米, BC 长是多少厘米?(32.8 厘米)
6.(省实天河)一个正方形的草地,边长是 3 米,在两个对角的顶点处各种一棵树, 树上各栓一只羊,绳长都是 3 米,问两只羊都能吃到草地的面积有多大?
五.课后自测练习
一座石英钟,时针长 2 分米,一昼夜针尖走了多少分米?
一个自行车轮胎的外直径是 70cm,如果每分钟车轮转 200 周,一小时能行多少千米?
(得数保留整数)
一个圆形花坛的直径是 20 米,现在要在花坛的周围铺一条 2 米宽的石板路,这条石板路的占地面积是多少平方米?
1209675521335有七根直径 5 厘米的塑料管,用一根橡皮筋把它们勒紧一捆(如左下图),此时橡皮筋的长度是多少厘米?
5.( 广大附中)下图半圆中,AB 为直径,C 为弧 AB 的中点,求阴影部分面积之和。(单位:厘米)
13423906527806.(天河省实)如图,用一块面积为 36 平方厘米的圆形铝板下料,从中裁出了 7 个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?
7.右图中 4 个圆的圆心是正方形的 4 个顶点,它们的公共点是该正方形的中心.如果每个圆
的半径都是 1 厘米,那么阴影部分的总面积是多少平方厘米?
第六讲 圆的周长和面积【答案】
课堂精讲
例 1. 填表
圆的半径(cm)
直径(cm)
面积( cm2 )
周长(cm)
12
24
452.16
75.36
4
8
50.24
25.12
12.5
25
490.625
78.5
例 2.设小圆的直径为 1 米,则大圆的周长为 3.14×2=6.28(米)
小圆的周长为 3.14×1×2=6.28(米)
【搭配课堂训练题】
7.周长增加( 10 )%。
8.三个小圆的周长之和是( 62.8 )厘米。
9. B 10.D
例 3. 周长为 3.14×5÷2+5=12.85(cm)
【搭配课堂训练题】 11.B 12.C
例 4.(1)C (2)圆桌面的面积是( 1.57 )平方米。
【搭配课堂训练题】
13.这个圆的面积是( 50.24 )平方厘米。 14.阴影部分的面积是 ( 37.5 ) cm2
15.A
1
例 5.解:两个弓形面积为 ?( 3)2 - 1 ? 3? 3 ? 9 ? - 9 ? 1.2825(平方厘米)
2 2 2
【搭配课堂训练题】
2 8 4
16.解:这个正方形的面积为 400 平方厘米。
讲练结合题
答:阴影部分的面积为 100 平方厘米。
答:阴影部分的面积为 18.84 平方厘米,周长为 62.8 厘米。
答:圆的面积为 31.4 平方分米。
答:图中阴影部分的面积为 16.82 平方厘米。
答:BC 长是 32.8 厘米。
答:两只羊都能吃到草地的面积 5.13 平方米。
课后自测练习
答:一昼夜针尖走了 25.12 分米.
答:一小时能行 26 千米.
答:这条石板路的占地面积是 138.16 平方米.
答:此时橡皮筋的长度是 45.7 厘米。
答:阴影部分面积之和为 63.585 平方厘米。
答:所余下的边角料的总面积是 8 平方厘米。
答:阴影部分的总面积是 10.28 平方厘米。
