高中物理人教版选修3.4 作业题 第十一章 机械振动 综合测试 Word版含解析
文档属性
| 名称 | 高中物理人教版选修3.4 作业题 第十一章 机械振动 综合测试 Word版含解析 |  | |
| 格式 | DOC | ||
| 文件大小 | 626.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-15 18:58:23 | ||
图片预览



文档简介
第十一章 《机械振动》综合测试
时间:90分钟 满分:100分
一、选择题(1~6为单选,7~10为多选,每小题4分,共40分)
1.一简谐运动的图象如图所示,在0.1~0.15 s这段时间内( B )
A.加速度增大,速度变小,加速度和速度的方向相同
B.加速度增大,速度变小,加速度和速度的方向相反
C.加速度减小,速度变大,加速度和速度的方向相反
D.加速度减小,速度变大,加速度和速度的方向相同
解析:由图象可知,在t=0.1 s时,质点位于平衡位置,t=0.15 s时,质点到达负向最大位移处,因此在t=0.1~0.15 s这段时间内,质点刚好处于由平衡位置向负向最大位移处运动的过程中,其位移为负值,且数值增大,速度逐渐减小,而加速度逐渐增大,为加速度逐渐增大的减速运动,故加速度方向与速度方向相反,因此选项B正确.
2.做简谐运动的单摆摆长不变,若摆球质量增加为原来的4倍,摆球经过平衡位置时速度减小为原来的,则单摆振动的( C )
A.频率、振幅都不变 B.频率、振幅都改变
C.频率不变,振幅改变 D.频率改变,振幅不变
解析:单摆振动的频率与摆长和所在地的重力加速度有关,与质量、振幅大小无关,题中单摆振动的频率不变;单摆振动过程中机械能守恒,振子在平衡位置的动能等于其在最大位移处的势能,因此,题中单摆的振幅改变,选项C正确.
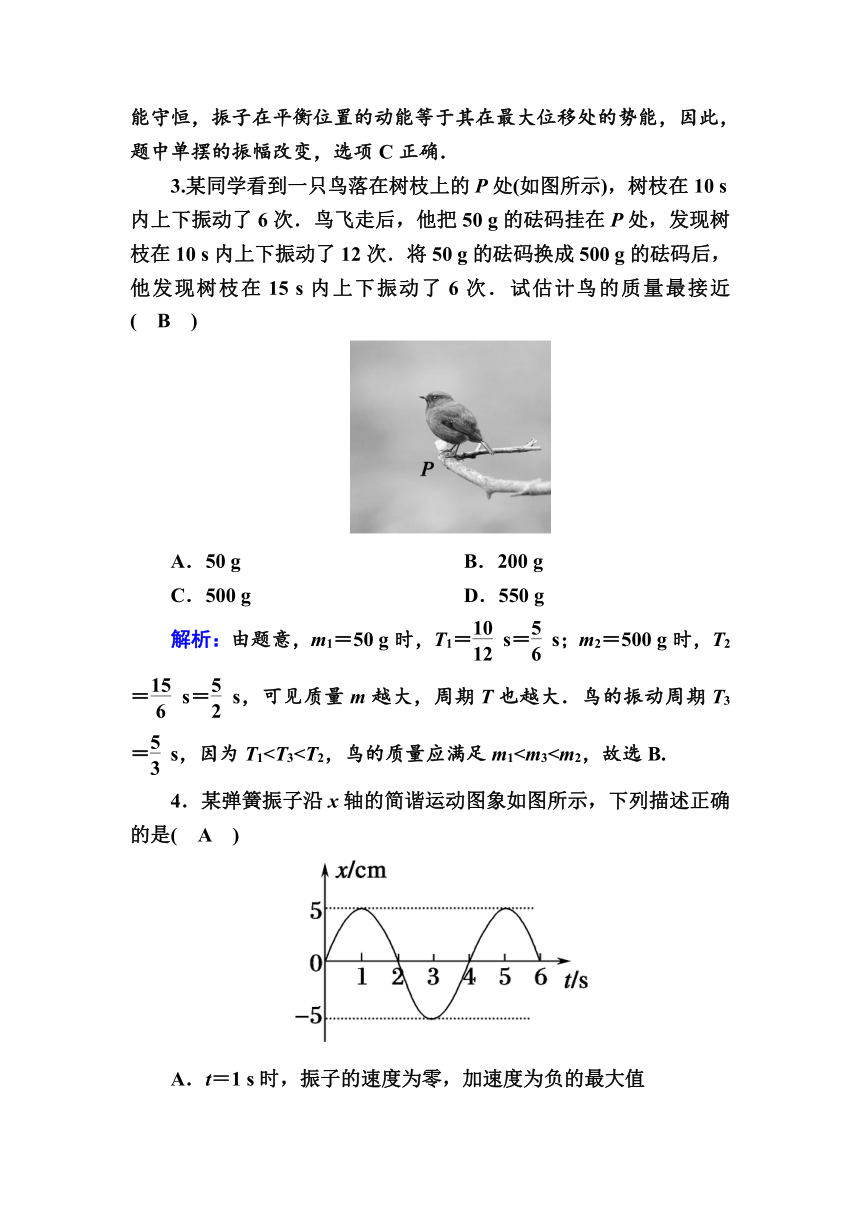
3.某同学看到一只鸟落在树枝上的P处(如图所示),树枝在10 s内上下振动了6次.鸟飞走后,他把50 g的砝码挂在P处,发现树枝在10 s内上下振动了12次.将50 g的砝码换成500 g的砝码后,他发现树枝在15 s内上下振动了6次.试估计鸟的质量最接近( B )
A.50 g B.200 g
C.500 g D.550 g
解析:由题意,m1=50 g时,T1= s= s;m2=500 g时,T2= s= s,可见质量m越大,周期T也越大.鸟的振动周期T3= s,因为T14.某弹簧振子沿x轴的简谐运动图象如图所示,下列描述正确的是( A )
A.t=1 s时,振子的速度为零,加速度为负的最大值
B.t=2 s时,振子的速度为负,加速度为正的最大值
C.t=3 s时,振子的速度为负的最大值,加速度为零
D.t=4 s时,振子的速度为正,加速度为负的最大值
解析:t=1 s时,振子在正的最大位移处,振子的速度为零,由a=-kx/m知,加速度为负的最大值,A项正确;t=2 s时,振子位于平衡位置,由a=-kx/m知,加速度为零,B项错误;t=3 s时,振子在负的最大位移处,由a=-kx/m知,加速度为正的最大值,C项错误;t=4 s时,振子位于平衡位置,由a=-kx/m知,加速度为零,D项错误.
5.一单摆由甲地移到乙地后,发现走时变快了,其变快的原因及调整的方法是( B )
A.g甲>g乙,将摆长缩短 B.g甲C.g甲g乙,将摆长放长
解析:走时变快了,说明周期T=2π变小了,即g乙>g甲,若要恢复原来的周期,则需把摆长变长,使不变.
6.如图所示,在光滑水平面上的弹簧振子,弹簧形变的最大限度为20 cm,图示P位置是弹簧振子处于自然伸长的位置,若将振子m向右拉动5 cm后由静止释放,经0.5 s振子m第一次回到P位置,关于该弹簧振子,下列说法正确的是( D )
A.该弹簧振子的振动频率为1 Hz
B.若向右拉动10 cm后由静止释放,经过1 s振子m第一次回到P位置
C.若向左推动8 cm后由静止释放,振子m两次经过P位置的时间间隔是2 s
D.在P位置给振子m任意一个向左或向右的初速度,只要位移不超过20 cm,总是经0.5 s速度就降为0
解析:本题考查简谐运动的周期性.由题意知,该弹簧振子振动周期为T=0.5×4 s=2 s,且以后不再变化,即弹簧振子固有周期为2 s,振动频率为0.5 Hz,所以B选项中应经过0.5 s第一次回到P位置,A、B选项错误;C选项中两次经过P位置的时间间隔为半个周期,是1 s,C选项错误,D选项正确.
7.如图所示为某鱼漂的示意图.当鱼漂静止时,水位恰好在O点.用手将鱼漂往下按,使水位到达M点.松手后,鱼漂会上下运动,水位在MN之间来回移动.不考虑阻力的影响,下列说法正确的是( AB )
A.鱼漂的运动是简谐运动
B.水位在O点时,鱼漂的速度最大
C.水位到达M点时,鱼漂具有向下的加速度
D.鱼漂由上往下运动时,速度越来越大
解析:设鱼漂的横截面积为S,O点以下的长度为h.当鱼漂静止时,水位恰好在O点,说明在O点浮力等于重力,即mg=ρgSh.可取O点所在位置为平衡位置,取竖直向下为正,当鱼漂被下按x时,水位在O点上方x处,此时合力为F合=mg-ρgS(h+x)=-ρgSx,同理可得水位在O点下方时也满足此式.因为ρ、g、S都是确定量,所以上述关系式满足简谐运动的条件(F合=-kx),鱼漂做的是简谐运动,选项A正确;O点是平衡位置,所以O点时鱼漂的速度最大,选项B正确;水位到达M点时,鱼漂具有向上的加速度,选项C错误;鱼漂由上往下运动时,可能加速也可能减速,选项D错误.
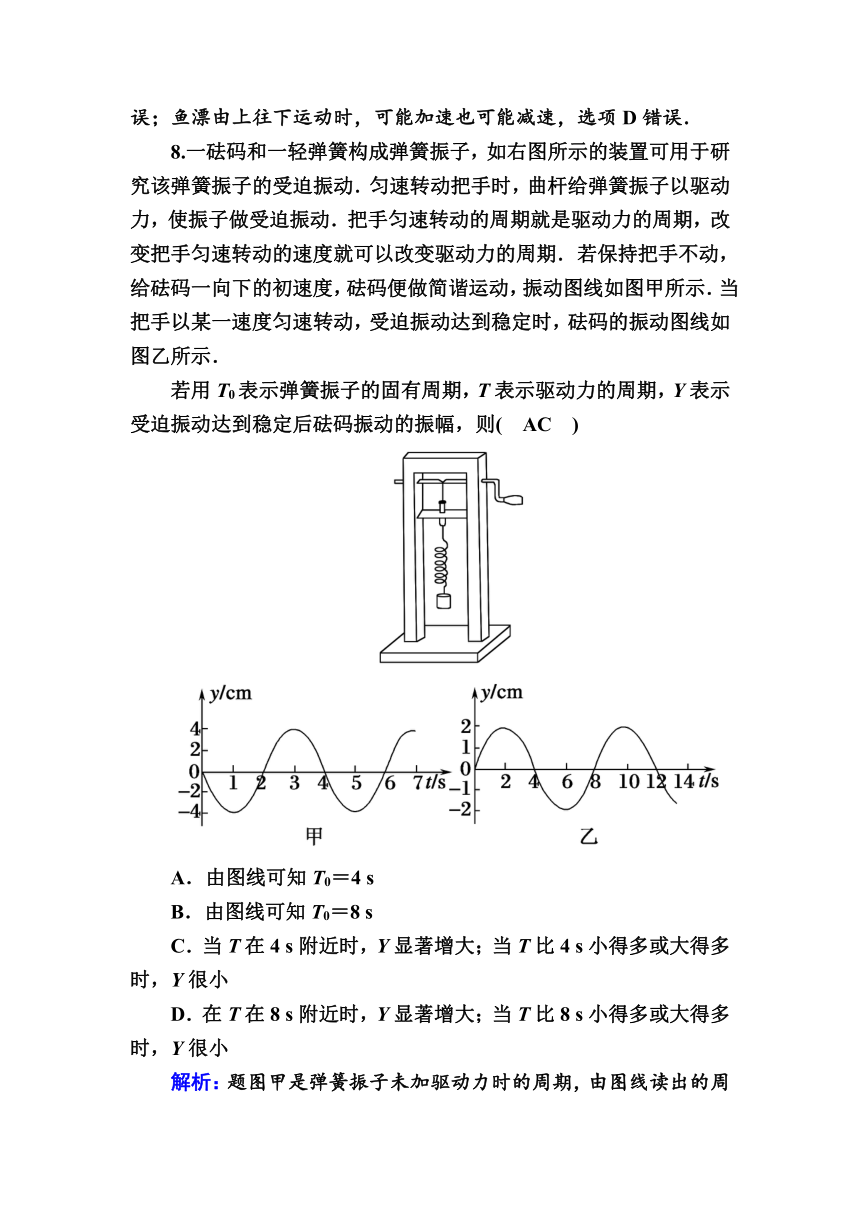
8.一砝码和一轻弹簧构成弹簧振子,如右图所示的装置可用于研究该弹簧振子的受迫振动.匀速转动把手时,曲杆给弹簧振子以驱动力,使振子做受迫振动.把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期.若保持把手不动,给砝码一向下的初速度,砝码便做简谐运动,振动图线如图甲所示.当把手以某一速度匀速转动,受迫振动达到稳定时,砝码的振动图线如图乙所示.
若用T0表示弹簧振子的固有周期,T表示驱动力的周期,Y表示受迫振动达到稳定后砝码振动的振幅,则( AC )
A.由图线可知T0=4 s
B.由图线可知T0=8 s
C.当T在4 s附近时,Y显著增大;当T比4 s小得多或大得多时,Y很小
D.在T在8 s附近时,Y显著增大;当T比8 s小得多或大得多时,Y很小
解析:题图甲是弹簧振子未加驱动力时的周期,由图线读出的周期为其振动的固有周期,即T0=4 s.题图乙是弹簧振子在驱动力作用下的振动图线,做受迫振动的物体,其振动的周期等于驱动力的周期,即T=8 s.当受迫振动的周期与驱动力的周期相同时,其振幅最大;周期差别越大,其运动振幅越小,由以上分析可知,正确选项为A、C.
9.如图所示,一根绷紧的水平绳上挂五个摆,其中A、E摆长均为l,先让A摆振动起来,其他各摆随后也跟着振动起来,则( ACD )
A.其他各摆振动周期跟A摆相同
B.其他各摆振动的振幅大小相等
C.其他各摆振动的振幅大小不同,E摆的振幅最大
D.B、C、D三摆振动的振幅大小不同,B摆的振幅最小
解析:A摆振动后迫使水平绳摆动.水平绳又迫使B、C、D、E四摆做受迫振动,由于物体做受迫振动的周期总是等于驱动力的周期,因此,B、C、D、E四摆的周期跟A摆相同.驱动力的频率等于A摆的固有频率fA==,其余四摆的固有频率与驱动力的频率关系是:fB=≈1.41fA,fC=≈0.82fA
fD=≈0.71fA,fE==fA
可见只有E摆的固有频率与驱动力的频率相等,它发生共振现象,其振幅最大,B、C、D三个摆均不发生共振,振幅各异,其中B摆的固有频率与驱动力的频率相差最大,所以它的振幅最小.
10.如图所示,在光滑杆下面铺一张可沿垂直杆方向匀速移动的白纸,一带有铅笔的弹簧振子在B、C两点间做机械振动,可以在白纸上留下痕迹.已知弹簧的劲度系数为k=10 N/m,振子的质量为0.5 kg,白纸移动速度为2 m/s,弹簧弹性势能的表达式Ep=ky2,不计一切摩擦.在一次弹簧振子实验中得到如图所示的图线,则下列说法正确的是( BC )
A.该弹簧振子的振幅为1 m
B.该弹簧振子的周期为1 s
C.该弹簧振子的最大加速度为10 m/s2
D.该弹簧振子的最大速度为2 m/s
解析:弹簧振子的振幅为振子偏离平衡位置的最大距离,所以该弹簧振子的振幅为A=0.5 m,选项A错误;由题图所示振子振动曲线可知,振动一个周期,白纸移动距离x=2 m,所以弹簧振子的周期为T==1 s,选项B正确;该振子所受最大回复力F=kA=5 N,最大加速度为a==10 m/s2,选项C正确;根据题述弹簧弹性势能的表达式为Ep=ky2,弹簧振子振动过程中机械能守恒,由mv=kA2可得最大速度为vm=A= m/s,选项D错误.
二、填空题(每小题9分,共18分)
11.某同学用实验的方法探究影响单摆周期的因素.
(1)他组装单摆时,在摆线上端的悬点处,用一块开有狭缝的橡皮夹牢摆线,再用铁架台的铁夹将橡皮夹紧,如图甲所示.这样做的目的是AC(填字母代号).
A.保证摆动过程中摆长不变
B.可使周期测量得更加准确
C.需要改变摆长时便于调节
D.保证摆球在同一竖直平面内摆动
(2)他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.999 0 m,再用游标卡尺测量摆球直径,结果如图乙所示,则该摆球的直径为12.0 mm,单摆摆长为0.993 0 m.
(3)下列振动图象真实地描述了对摆长约为1 m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin 5°=0.087,sin 15°=0.26,这四种操作过程合乎实验要求且误差最小的是A(填字母代号).
解析:(1)夹牢摆线可以使摆动过程中摆线长度不变,夹子可以根据需要改变摆长,故选择A、C;
(2)游标尺的0刻线与主尺12 mm对齐,10刻线与主尺刻线对齐,所以读数为12.0 mm;摆长L=0.999 0 m- m=0.993 0 m;
(3)sin5°=0.087,摆长为1 m,所以振幅约为8.7 cm,C、D误差较大;又振子在平衡位置开始计时误差较小,所以t=0时,振子应在平衡位置,故选择A.
12.用单摆测定重力加速度的实验装置如图甲所示.
(1)组装单摆时,应在下列器材中选用AD(选填选项前的字母).
A.长度为1 m左右的细线
B.长度为30 cm左右的细线
C.直径为1.8 cm的塑料球
D.直径为1.8 cm的铁球
(2)测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=(用L、n、t表示).
(3)下表是某同学记录的3组实验数据,并做了部分计算处理.
组次 1 2 3
摆长L/cm 80.00 90.00 100.00
50次全振动时间t/s 90.0 95.5 100.5
振动周期T/s 1.80 1.91
重力加速度g/(m·s-2) 9.74 9.73
请计算出第3组实验中的T=2.01 s,g=9.76 m/s2.
(4)用多组实验数据作出T2 L图象,也可以求出重力加速度g.已知三位同学作出的T2 L图线的示意图如图乙中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值.则相对于图线b,下列分析正确的是B(选填选项前的字母).
A.出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L
B.出现图线c的原因可能是误将49次全振动记为50次
C.图线c对应的g值小于图线b对应的g值
(5)某同学在家里测重力加速度.他找到细线和铁锁,制成一个单摆,如图丙所示.由于家里只有一根量程为30 cm的刻度尺,于是他在细线上的A点做了一个标记,使得悬点O到A点间的细线长度小于刻度尺量程.保持该标记以下的细线长度不变,通过改变O、A间细线长度以改变摆长.实验中,当O、A间细线的长度分别为l1、l2时,测得相应单摆的周期为T1、T2.由此可得重力加速度g=(用l1、l2、T1、T2表示).
解析:(1)单摆模型需要满足的条件是,摆线的长度远大于小球直径,小球的密度越大越好,这样可以忽略空气阻力.
(2)周期T=,结合T=2π,推出g=.
(3)周期T===2.01 s,
由T=2π,解出g=9.76 m/s2.
(4)由T=2π,两边平方后可知T2 L是过原点的直线,b为正确的图象,a与b相比,周期相同时,摆长更短,说明a对应测量的摆长偏小;c与b相比,摆长相同时,周期偏小,可能是多记录了振动次数.
(5)设A到铁锁重心的距离为l,则第1、2次的摆长分别为l+l1、l+l2,由T1=2π,T2=2π,联立解得g=.
三、计算题(共42分)
13.(8分)一水平弹簧振子做简谐运动,其位移和时间关系如图所示.
(1)求t=0.25×10-2 s时刻的位移.
(2)从t=0到t=8.5×10-2 s的时间内,质点的路程、位移各为多大?
答案:(1)-1.414 cm (2)34 cm 0
解析:(1)由图象可知T=2×10-2 s,则ω==100π,横坐标t=0.25×10-2 s时,所对应的纵坐标x=-Acosωt=-2cos(100π×0.25×10-2) cm≈-1.414 cm.
(2)因振动是变速运动,因此只能利用其周期性求解.即一个周期内通过的路程为4个振幅,本题中Δt=8.5×10-2 s=T,所以通过的路程为×4A=17A=17×2 cm=34 cm,经个周期振子回到平衡位置,位移为零.
14.(12分)如图所示,摆长为1 m的单摆做简谐运动,C点在悬点O的正下方,D点与C点相距2 m,C、D之间是光滑水平面.当摆球A摆到左侧最大位移处时,小球B从D点以某一速度匀速地向C点运动,A、B两球在C点迎面相遇,求小球B的速度大小.(g取9.8 m/s2)
答案: m/s(n=0,1,2,…)
解析:单摆做简谐运动的周期为T=2π=2 s,A球运动到C点且速度向左经历的时间为t=T=(2n+1.5) s
(n=0,1,2,…),则B球的速度为v== m/s= m/s(n=0,1,2,…).
15.(12分)在心电图仪、地震仪等仪器工作过程中,要进行振动记录,如图甲所示是一个常用的记录方法,在弹簧振子的小球上安装一支记录用笔P,在下面放一条白纸带.当小球振动时,匀速拉动纸带(纸带运动方向与振子振动方向垂直),笔就在纸带上画出一条曲线,如图乙所示.
(1)若匀速拉动纸带的速度为1 m/s,则由图乙中数据算出振子的振动周期为多少?
(2)作出P的振动图象.
(3)若拉动纸带做匀加速运动,且振子振动周期与原来相同,由图丙中的数据求纸带的加速度大小.
答案:(1)0.2 s (2)如图所示 (3)1.0 m/s2
解析:(1)由题图乙可知,当纸带匀速前进20 cm时,弹簧振子恰好完成一次全振动,由v=,可得t== s,所以T=0.2 s;
(2)由题图乙可以看出P的振幅为2 cm,振动图象如答案图所示;
(3)当纸带做匀加速直线运动时,振子振动周期仍为0.2 s,由丙图可知,两个相邻0.2 s时间内,纸带运动的距离分别为0.21 m、0.25 m,由Δx=aT2,得a= m/s2=1.0 m/s2.
16.(10分)如图所示,质量为m=0.5 kg的物体放在质量为M=4.5 kg的平台上,随平台上、下做简谐运动.设在简谐运动过程中,二者始终保持相对静止.已知弹簧的劲度系数为k=400 N/m,振幅为A=0.1 m.试求:
(1)二者一起运动到最低点时,物体对平台的压力大小;
(2)二者一起运动最高点时,物体对平台的压力大小.(g取10 m/s2)
答案:(1)9 N (2)1 N
解析:(1)在平衡位置,设弹簧压缩量为x,有(M+m)g=kx,解得x=0.125 m.
在最低点,设物体对平台压力大小为F1,由牛顿第三定律可知,平台对物体的支持力大小也为F1,对整体k(x+A)-(M+m)g=(M+m)a1.对m,F1-mg=ma1,解得a1=8 m/s2,F1=9 N.
(2)在最高点,设物体对平台压力大小为F2,对整体(M+m)g-k(x-A)=(M+m)a2.对m,mg-F2=ma2,
解得a2=8 m/s2,F2=1 N.
时间:90分钟 满分:100分
一、选择题(1~6为单选,7~10为多选,每小题4分,共40分)
1.一简谐运动的图象如图所示,在0.1~0.15 s这段时间内( B )
A.加速度增大,速度变小,加速度和速度的方向相同
B.加速度增大,速度变小,加速度和速度的方向相反
C.加速度减小,速度变大,加速度和速度的方向相反
D.加速度减小,速度变大,加速度和速度的方向相同
解析:由图象可知,在t=0.1 s时,质点位于平衡位置,t=0.15 s时,质点到达负向最大位移处,因此在t=0.1~0.15 s这段时间内,质点刚好处于由平衡位置向负向最大位移处运动的过程中,其位移为负值,且数值增大,速度逐渐减小,而加速度逐渐增大,为加速度逐渐增大的减速运动,故加速度方向与速度方向相反,因此选项B正确.
2.做简谐运动的单摆摆长不变,若摆球质量增加为原来的4倍,摆球经过平衡位置时速度减小为原来的,则单摆振动的( C )
A.频率、振幅都不变 B.频率、振幅都改变
C.频率不变,振幅改变 D.频率改变,振幅不变
解析:单摆振动的频率与摆长和所在地的重力加速度有关,与质量、振幅大小无关,题中单摆振动的频率不变;单摆振动过程中机械能守恒,振子在平衡位置的动能等于其在最大位移处的势能,因此,题中单摆的振幅改变,选项C正确.
3.某同学看到一只鸟落在树枝上的P处(如图所示),树枝在10 s内上下振动了6次.鸟飞走后,他把50 g的砝码挂在P处,发现树枝在10 s内上下振动了12次.将50 g的砝码换成500 g的砝码后,他发现树枝在15 s内上下振动了6次.试估计鸟的质量最接近( B )
A.50 g B.200 g
C.500 g D.550 g
解析:由题意,m1=50 g时,T1= s= s;m2=500 g时,T2= s= s,可见质量m越大,周期T也越大.鸟的振动周期T3= s,因为T1
A.t=1 s时,振子的速度为零,加速度为负的最大值
B.t=2 s时,振子的速度为负,加速度为正的最大值
C.t=3 s时,振子的速度为负的最大值,加速度为零
D.t=4 s时,振子的速度为正,加速度为负的最大值
解析:t=1 s时,振子在正的最大位移处,振子的速度为零,由a=-kx/m知,加速度为负的最大值,A项正确;t=2 s时,振子位于平衡位置,由a=-kx/m知,加速度为零,B项错误;t=3 s时,振子在负的最大位移处,由a=-kx/m知,加速度为正的最大值,C项错误;t=4 s时,振子位于平衡位置,由a=-kx/m知,加速度为零,D项错误.
5.一单摆由甲地移到乙地后,发现走时变快了,其变快的原因及调整的方法是( B )
A.g甲>g乙,将摆长缩短 B.g甲
解析:走时变快了,说明周期T=2π变小了,即g乙>g甲,若要恢复原来的周期,则需把摆长变长,使不变.
6.如图所示,在光滑水平面上的弹簧振子,弹簧形变的最大限度为20 cm,图示P位置是弹簧振子处于自然伸长的位置,若将振子m向右拉动5 cm后由静止释放,经0.5 s振子m第一次回到P位置,关于该弹簧振子,下列说法正确的是( D )
A.该弹簧振子的振动频率为1 Hz
B.若向右拉动10 cm后由静止释放,经过1 s振子m第一次回到P位置
C.若向左推动8 cm后由静止释放,振子m两次经过P位置的时间间隔是2 s
D.在P位置给振子m任意一个向左或向右的初速度,只要位移不超过20 cm,总是经0.5 s速度就降为0
解析:本题考查简谐运动的周期性.由题意知,该弹簧振子振动周期为T=0.5×4 s=2 s,且以后不再变化,即弹簧振子固有周期为2 s,振动频率为0.5 Hz,所以B选项中应经过0.5 s第一次回到P位置,A、B选项错误;C选项中两次经过P位置的时间间隔为半个周期,是1 s,C选项错误,D选项正确.
7.如图所示为某鱼漂的示意图.当鱼漂静止时,水位恰好在O点.用手将鱼漂往下按,使水位到达M点.松手后,鱼漂会上下运动,水位在MN之间来回移动.不考虑阻力的影响,下列说法正确的是( AB )
A.鱼漂的运动是简谐运动
B.水位在O点时,鱼漂的速度最大
C.水位到达M点时,鱼漂具有向下的加速度
D.鱼漂由上往下运动时,速度越来越大
解析:设鱼漂的横截面积为S,O点以下的长度为h.当鱼漂静止时,水位恰好在O点,说明在O点浮力等于重力,即mg=ρgSh.可取O点所在位置为平衡位置,取竖直向下为正,当鱼漂被下按x时,水位在O点上方x处,此时合力为F合=mg-ρgS(h+x)=-ρgSx,同理可得水位在O点下方时也满足此式.因为ρ、g、S都是确定量,所以上述关系式满足简谐运动的条件(F合=-kx),鱼漂做的是简谐运动,选项A正确;O点是平衡位置,所以O点时鱼漂的速度最大,选项B正确;水位到达M点时,鱼漂具有向上的加速度,选项C错误;鱼漂由上往下运动时,可能加速也可能减速,选项D错误.
8.一砝码和一轻弹簧构成弹簧振子,如右图所示的装置可用于研究该弹簧振子的受迫振动.匀速转动把手时,曲杆给弹簧振子以驱动力,使振子做受迫振动.把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期.若保持把手不动,给砝码一向下的初速度,砝码便做简谐运动,振动图线如图甲所示.当把手以某一速度匀速转动,受迫振动达到稳定时,砝码的振动图线如图乙所示.
若用T0表示弹簧振子的固有周期,T表示驱动力的周期,Y表示受迫振动达到稳定后砝码振动的振幅,则( AC )
A.由图线可知T0=4 s
B.由图线可知T0=8 s
C.当T在4 s附近时,Y显著增大;当T比4 s小得多或大得多时,Y很小
D.在T在8 s附近时,Y显著增大;当T比8 s小得多或大得多时,Y很小
解析:题图甲是弹簧振子未加驱动力时的周期,由图线读出的周期为其振动的固有周期,即T0=4 s.题图乙是弹簧振子在驱动力作用下的振动图线,做受迫振动的物体,其振动的周期等于驱动力的周期,即T=8 s.当受迫振动的周期与驱动力的周期相同时,其振幅最大;周期差别越大,其运动振幅越小,由以上分析可知,正确选项为A、C.
9.如图所示,一根绷紧的水平绳上挂五个摆,其中A、E摆长均为l,先让A摆振动起来,其他各摆随后也跟着振动起来,则( ACD )
A.其他各摆振动周期跟A摆相同
B.其他各摆振动的振幅大小相等
C.其他各摆振动的振幅大小不同,E摆的振幅最大
D.B、C、D三摆振动的振幅大小不同,B摆的振幅最小
解析:A摆振动后迫使水平绳摆动.水平绳又迫使B、C、D、E四摆做受迫振动,由于物体做受迫振动的周期总是等于驱动力的周期,因此,B、C、D、E四摆的周期跟A摆相同.驱动力的频率等于A摆的固有频率fA==,其余四摆的固有频率与驱动力的频率关系是:fB=≈1.41fA,fC=≈0.82fA
fD=≈0.71fA,fE==fA
可见只有E摆的固有频率与驱动力的频率相等,它发生共振现象,其振幅最大,B、C、D三个摆均不发生共振,振幅各异,其中B摆的固有频率与驱动力的频率相差最大,所以它的振幅最小.
10.如图所示,在光滑杆下面铺一张可沿垂直杆方向匀速移动的白纸,一带有铅笔的弹簧振子在B、C两点间做机械振动,可以在白纸上留下痕迹.已知弹簧的劲度系数为k=10 N/m,振子的质量为0.5 kg,白纸移动速度为2 m/s,弹簧弹性势能的表达式Ep=ky2,不计一切摩擦.在一次弹簧振子实验中得到如图所示的图线,则下列说法正确的是( BC )
A.该弹簧振子的振幅为1 m
B.该弹簧振子的周期为1 s
C.该弹簧振子的最大加速度为10 m/s2
D.该弹簧振子的最大速度为2 m/s
解析:弹簧振子的振幅为振子偏离平衡位置的最大距离,所以该弹簧振子的振幅为A=0.5 m,选项A错误;由题图所示振子振动曲线可知,振动一个周期,白纸移动距离x=2 m,所以弹簧振子的周期为T==1 s,选项B正确;该振子所受最大回复力F=kA=5 N,最大加速度为a==10 m/s2,选项C正确;根据题述弹簧弹性势能的表达式为Ep=ky2,弹簧振子振动过程中机械能守恒,由mv=kA2可得最大速度为vm=A= m/s,选项D错误.
二、填空题(每小题9分,共18分)
11.某同学用实验的方法探究影响单摆周期的因素.
(1)他组装单摆时,在摆线上端的悬点处,用一块开有狭缝的橡皮夹牢摆线,再用铁架台的铁夹将橡皮夹紧,如图甲所示.这样做的目的是AC(填字母代号).
A.保证摆动过程中摆长不变
B.可使周期测量得更加准确
C.需要改变摆长时便于调节
D.保证摆球在同一竖直平面内摆动
(2)他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.999 0 m,再用游标卡尺测量摆球直径,结果如图乙所示,则该摆球的直径为12.0 mm,单摆摆长为0.993 0 m.
(3)下列振动图象真实地描述了对摆长约为1 m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin 5°=0.087,sin 15°=0.26,这四种操作过程合乎实验要求且误差最小的是A(填字母代号).
解析:(1)夹牢摆线可以使摆动过程中摆线长度不变,夹子可以根据需要改变摆长,故选择A、C;
(2)游标尺的0刻线与主尺12 mm对齐,10刻线与主尺刻线对齐,所以读数为12.0 mm;摆长L=0.999 0 m- m=0.993 0 m;
(3)sin5°=0.087,摆长为1 m,所以振幅约为8.7 cm,C、D误差较大;又振子在平衡位置开始计时误差较小,所以t=0时,振子应在平衡位置,故选择A.
12.用单摆测定重力加速度的实验装置如图甲所示.
(1)组装单摆时,应在下列器材中选用AD(选填选项前的字母).
A.长度为1 m左右的细线
B.长度为30 cm左右的细线
C.直径为1.8 cm的塑料球
D.直径为1.8 cm的铁球
(2)测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=(用L、n、t表示).
(3)下表是某同学记录的3组实验数据,并做了部分计算处理.
组次 1 2 3
摆长L/cm 80.00 90.00 100.00
50次全振动时间t/s 90.0 95.5 100.5
振动周期T/s 1.80 1.91
重力加速度g/(m·s-2) 9.74 9.73
请计算出第3组实验中的T=2.01 s,g=9.76 m/s2.
(4)用多组实验数据作出T2 L图象,也可以求出重力加速度g.已知三位同学作出的T2 L图线的示意图如图乙中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值.则相对于图线b,下列分析正确的是B(选填选项前的字母).
A.出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L
B.出现图线c的原因可能是误将49次全振动记为50次
C.图线c对应的g值小于图线b对应的g值
(5)某同学在家里测重力加速度.他找到细线和铁锁,制成一个单摆,如图丙所示.由于家里只有一根量程为30 cm的刻度尺,于是他在细线上的A点做了一个标记,使得悬点O到A点间的细线长度小于刻度尺量程.保持该标记以下的细线长度不变,通过改变O、A间细线长度以改变摆长.实验中,当O、A间细线的长度分别为l1、l2时,测得相应单摆的周期为T1、T2.由此可得重力加速度g=(用l1、l2、T1、T2表示).
解析:(1)单摆模型需要满足的条件是,摆线的长度远大于小球直径,小球的密度越大越好,这样可以忽略空气阻力.
(2)周期T=,结合T=2π,推出g=.
(3)周期T===2.01 s,
由T=2π,解出g=9.76 m/s2.
(4)由T=2π,两边平方后可知T2 L是过原点的直线,b为正确的图象,a与b相比,周期相同时,摆长更短,说明a对应测量的摆长偏小;c与b相比,摆长相同时,周期偏小,可能是多记录了振动次数.
(5)设A到铁锁重心的距离为l,则第1、2次的摆长分别为l+l1、l+l2,由T1=2π,T2=2π,联立解得g=.
三、计算题(共42分)
13.(8分)一水平弹簧振子做简谐运动,其位移和时间关系如图所示.
(1)求t=0.25×10-2 s时刻的位移.
(2)从t=0到t=8.5×10-2 s的时间内,质点的路程、位移各为多大?
答案:(1)-1.414 cm (2)34 cm 0
解析:(1)由图象可知T=2×10-2 s,则ω==100π,横坐标t=0.25×10-2 s时,所对应的纵坐标x=-Acosωt=-2cos(100π×0.25×10-2) cm≈-1.414 cm.
(2)因振动是变速运动,因此只能利用其周期性求解.即一个周期内通过的路程为4个振幅,本题中Δt=8.5×10-2 s=T,所以通过的路程为×4A=17A=17×2 cm=34 cm,经个周期振子回到平衡位置,位移为零.
14.(12分)如图所示,摆长为1 m的单摆做简谐运动,C点在悬点O的正下方,D点与C点相距2 m,C、D之间是光滑水平面.当摆球A摆到左侧最大位移处时,小球B从D点以某一速度匀速地向C点运动,A、B两球在C点迎面相遇,求小球B的速度大小.(g取9.8 m/s2)
答案: m/s(n=0,1,2,…)
解析:单摆做简谐运动的周期为T=2π=2 s,A球运动到C点且速度向左经历的时间为t=T=(2n+1.5) s
(n=0,1,2,…),则B球的速度为v== m/s= m/s(n=0,1,2,…).
15.(12分)在心电图仪、地震仪等仪器工作过程中,要进行振动记录,如图甲所示是一个常用的记录方法,在弹簧振子的小球上安装一支记录用笔P,在下面放一条白纸带.当小球振动时,匀速拉动纸带(纸带运动方向与振子振动方向垂直),笔就在纸带上画出一条曲线,如图乙所示.
(1)若匀速拉动纸带的速度为1 m/s,则由图乙中数据算出振子的振动周期为多少?
(2)作出P的振动图象.
(3)若拉动纸带做匀加速运动,且振子振动周期与原来相同,由图丙中的数据求纸带的加速度大小.
答案:(1)0.2 s (2)如图所示 (3)1.0 m/s2
解析:(1)由题图乙可知,当纸带匀速前进20 cm时,弹簧振子恰好完成一次全振动,由v=,可得t== s,所以T=0.2 s;
(2)由题图乙可以看出P的振幅为2 cm,振动图象如答案图所示;
(3)当纸带做匀加速直线运动时,振子振动周期仍为0.2 s,由丙图可知,两个相邻0.2 s时间内,纸带运动的距离分别为0.21 m、0.25 m,由Δx=aT2,得a= m/s2=1.0 m/s2.
16.(10分)如图所示,质量为m=0.5 kg的物体放在质量为M=4.5 kg的平台上,随平台上、下做简谐运动.设在简谐运动过程中,二者始终保持相对静止.已知弹簧的劲度系数为k=400 N/m,振幅为A=0.1 m.试求:
(1)二者一起运动到最低点时,物体对平台的压力大小;
(2)二者一起运动最高点时,物体对平台的压力大小.(g取10 m/s2)
答案:(1)9 N (2)1 N
解析:(1)在平衡位置,设弹簧压缩量为x,有(M+m)g=kx,解得x=0.125 m.
在最低点,设物体对平台压力大小为F1,由牛顿第三定律可知,平台对物体的支持力大小也为F1,对整体k(x+A)-(M+m)g=(M+m)a1.对m,F1-mg=ma1,解得a1=8 m/s2,F1=9 N.
(2)在最高点,设物体对平台压力大小为F2,对整体(M+m)g-k(x-A)=(M+m)a2.对m,mg-F2=ma2,
解得a2=8 m/s2,F2=1 N.
