等腰三角形的性质讲学稿
图片预览


文档简介
等腰三角形的性质讲学稿
蔡博
教学目标
1.初步掌握等腰三角形的性质及简单应用.
2.理解等腰三角形和等边三角形的性质定理之间的关系.
3.培养分类讨论、方程的思想和添加辅助线解决问题的能力.
教学重点和难点
重点是等腰三角形性质的应用;难点是等腰三角形的“三线合一”性质的灵活运用.
教学过程设计
创设情景,建模引入
一、探索并证明等腰三角形的三条性质
1.探索并证明等腰三角形底角的性质.
师生拿出事先准备好的两个三角形模型:一个等腰三角形、一个不等边三角形,做以下工作.
(1)复习等腰三角形的有关概念.
让学生叙述等腰三角形的定义及各部分名称.
(2)观察猜想、实验验证等腰三角形的性质.
让学生观察对比两个三角形,猜想等腰三角形的底角的性质,并用测量、折叠等手段加以验证,写出相应猜想.
等腰三角形的两个底角相等,并可简写成“等边对等角”(性质1). (3)教师要求学生根据猜想的结论画出相应的图形,写出已知和求证.
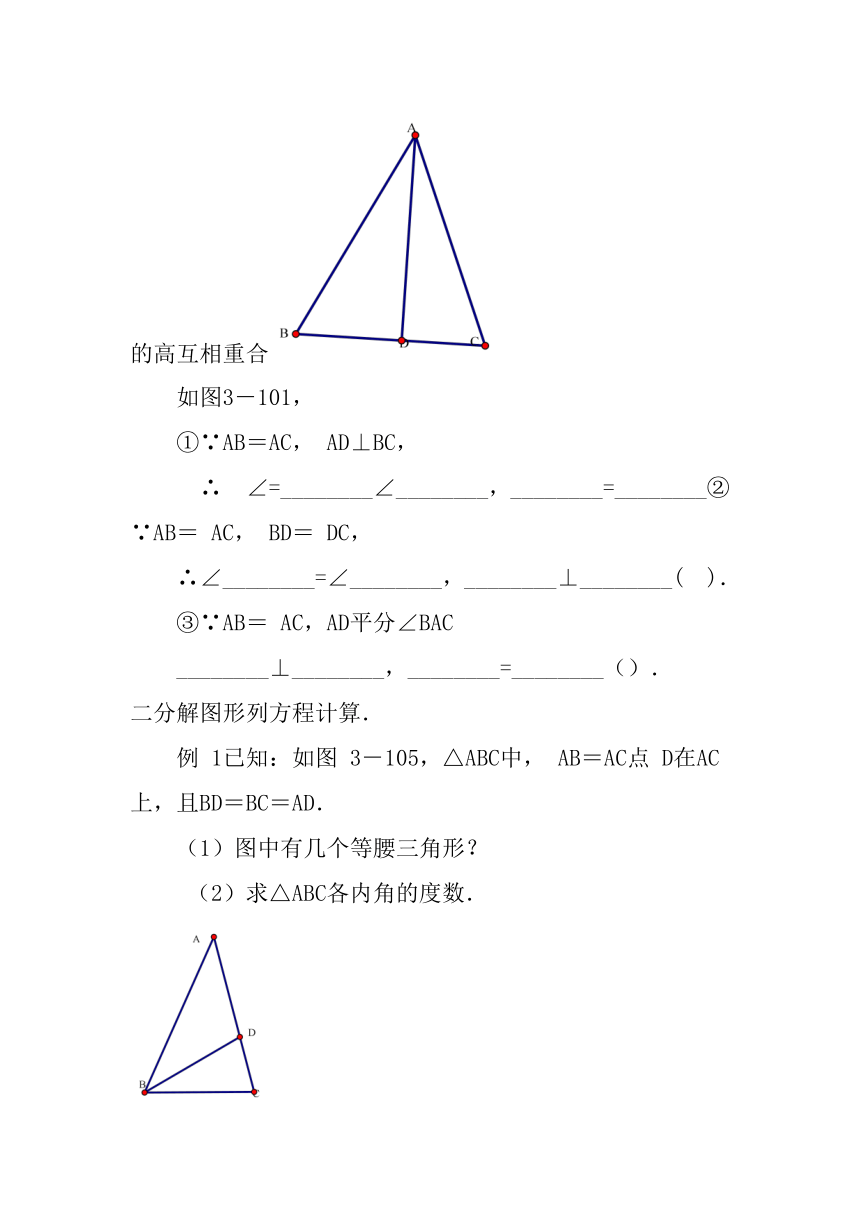
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
如图3-101,
①∵AB=AC, AD⊥BC,
∴ ∠=________∠________,________=________②∵AB= AC, BD= DC,
∴∠________=∠________,________⊥________( ).
③∵AB= AC,AD平分∠BAC
________⊥________,________=________().
二分解图形列方程计算.
例 1已知:如图 3-105,△ABC中, AB=AC点 D在AC上,且BD=BC=AD.
(1)图中有几个等腰三角形?
(2)求△ABC各内角的度数.
三,自我归纳,交流,探究
1.如图,△ABC是等腰三角形AB=AC,∠BAC=90°AD是底边BC上的高,标出∠B,∠C,∠BAD,的度数。图中有哪些相等的线段?
2.如图,在△ABC中,AB=AD=DC,∠BAD=26°求∠B和∠C的度数。
四,提高题
如图,已知△ABC中,AB=AC,BE=CF,求证:DE=DF.
已知,如图,在梯形ABCD中,AD∥BC,DF∥AB,CF平分∠BCD,BC=DC,BF的延长线交DC于E。求证:(1)△BFC≌△DFC,(2)AD=DE
如图,已知,△ACB中,∠ACB=90°,E和D两点在AB上,AD=AC,B=BC,求∠EDC的度数
如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
求证:AE=BE;
若∠AEC=45°,AC=1,求CE的长。
五,自我测试
1.等腰三角形的腰长是底边的2倍,底边等于12cm,则三角形的周长为—— cm 2.等腰三角形顶角为80°,则一腰上的高与底边所夹的角的度数为____度 3.等腰三角形的底角是65°,顶角为________. 4.等腰三角形的一个内角为100°,则它的其余各角的度数分别为_______. 5. P为等边△ABC所在平面上一点,且△PAB,△PBC,△PCA都是等腰三角形,这样的点P有_______个. 6. 等腰三角形的顶角等于一个底角的4倍时, 则顶角为_________度. 7. 已知如图,A、D、C在一条直线上AB=BD=CD, ∠C=40°,则∠ABD=_
蔡博
教学目标
1.初步掌握等腰三角形的性质及简单应用.
2.理解等腰三角形和等边三角形的性质定理之间的关系.
3.培养分类讨论、方程的思想和添加辅助线解决问题的能力.
教学重点和难点
重点是等腰三角形性质的应用;难点是等腰三角形的“三线合一”性质的灵活运用.
教学过程设计
创设情景,建模引入
一、探索并证明等腰三角形的三条性质
1.探索并证明等腰三角形底角的性质.
师生拿出事先准备好的两个三角形模型:一个等腰三角形、一个不等边三角形,做以下工作.
(1)复习等腰三角形的有关概念.
让学生叙述等腰三角形的定义及各部分名称.
(2)观察猜想、实验验证等腰三角形的性质.
让学生观察对比两个三角形,猜想等腰三角形的底角的性质,并用测量、折叠等手段加以验证,写出相应猜想.
等腰三角形的两个底角相等,并可简写成“等边对等角”(性质1). (3)教师要求学生根据猜想的结论画出相应的图形,写出已知和求证.
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
如图3-101,
①∵AB=AC, AD⊥BC,
∴ ∠=________∠________,________=________②∵AB= AC, BD= DC,
∴∠________=∠________,________⊥________( ).
③∵AB= AC,AD平分∠BAC
________⊥________,________=________().
二分解图形列方程计算.
例 1已知:如图 3-105,△ABC中, AB=AC点 D在AC上,且BD=BC=AD.
(1)图中有几个等腰三角形?
(2)求△ABC各内角的度数.
三,自我归纳,交流,探究
1.如图,△ABC是等腰三角形AB=AC,∠BAC=90°AD是底边BC上的高,标出∠B,∠C,∠BAD,的度数。图中有哪些相等的线段?
2.如图,在△ABC中,AB=AD=DC,∠BAD=26°求∠B和∠C的度数。
四,提高题
如图,已知△ABC中,AB=AC,BE=CF,求证:DE=DF.
已知,如图,在梯形ABCD中,AD∥BC,DF∥AB,CF平分∠BCD,BC=DC,BF的延长线交DC于E。求证:(1)△BFC≌△DFC,(2)AD=DE
如图,已知,△ACB中,∠ACB=90°,E和D两点在AB上,AD=AC,B=BC,求∠EDC的度数
如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
求证:AE=BE;
若∠AEC=45°,AC=1,求CE的长。
五,自我测试
1.等腰三角形的腰长是底边的2倍,底边等于12cm,则三角形的周长为—— cm 2.等腰三角形顶角为80°,则一腰上的高与底边所夹的角的度数为____度 3.等腰三角形的底角是65°,顶角为________. 4.等腰三角形的一个内角为100°,则它的其余各角的度数分别为_______. 5. P为等边△ABC所在平面上一点,且△PAB,△PBC,△PCA都是等腰三角形,这样的点P有_______个. 6. 等腰三角形的顶角等于一个底角的4倍时, 则顶角为_________度. 7. 已知如图,A、D、C在一条直线上AB=BD=CD, ∠C=40°,则∠ABD=_
