人教版数学八年级上册第十三章13.1轴对称课件(029张PPT)
文档属性
| 名称 | 人教版数学八年级上册第十三章13.1轴对称课件(029张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
轴对称
新知引入
议一议:观察下列图片,说一说它们的共同特征.
新知引入
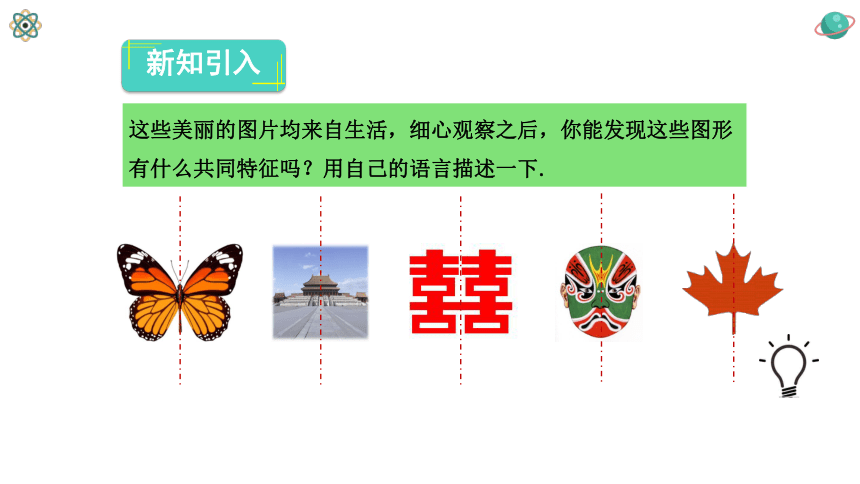
这些美丽的图片均来自生活,细心观察之后,你能发现这些图形有什么共同特征吗?用自己的语言描述一下.
新知讲解
如果一个图形沿一条直线折叠,两直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线即折痕所在的直线就是它的对称轴.
轴对称和轴对称图形
1
新知讲解
我们学过的图形中,你知道哪些图形是轴对称图形吗?
下面的图形是轴对称图形吗 如果是,你能指出它的对称轴吗
线段、角、等腰三角形、圆、正方形
新知应用
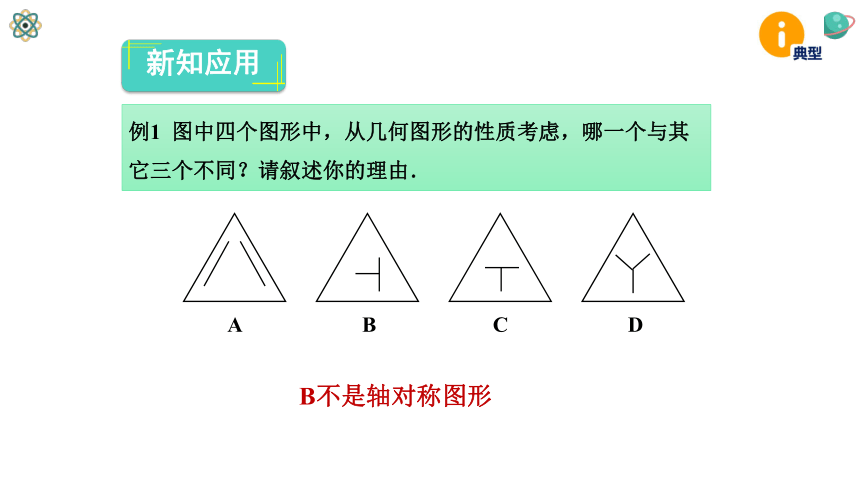
例1 图中四个图形中,从几何图形的性质考虑,哪一个与其它三个不同?请叙述你的理由.
A
B
C
D
B不是轴对称图形
新知应用
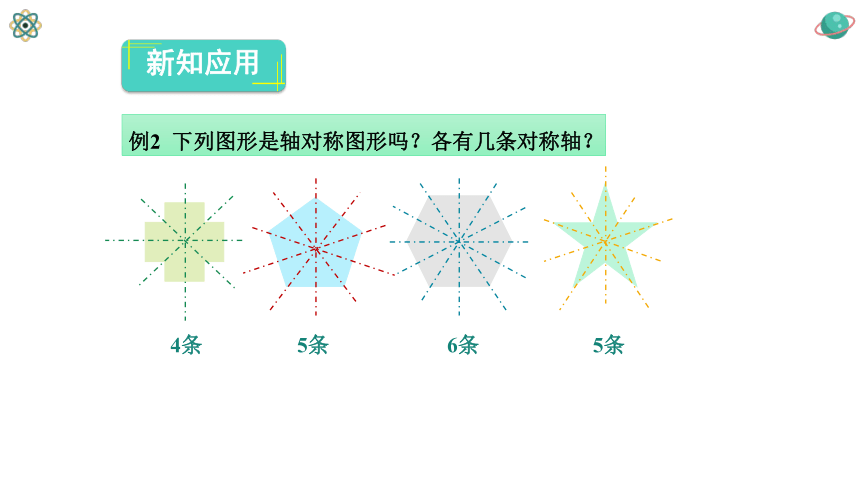
例2 下列图形是轴对称图形吗?各有几条对称轴?
4条
5条
6条
5条
新知引入
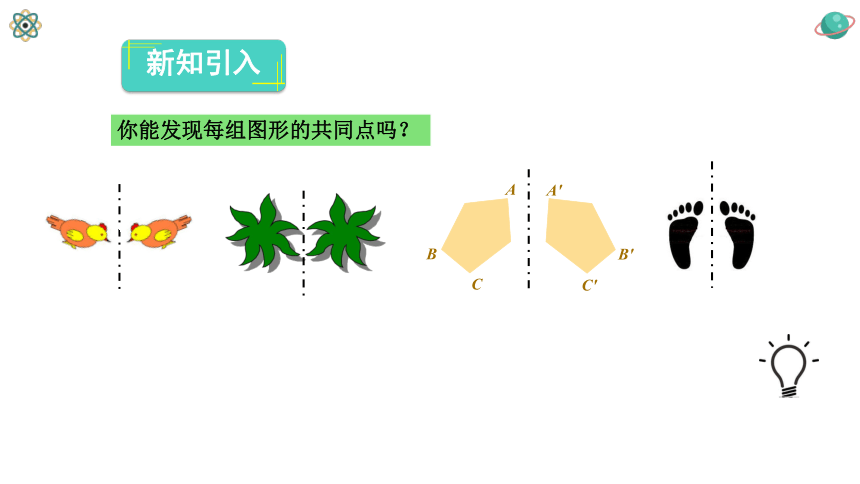
你能发现每组图形的共同点吗?
A
B
C
A′
B′
C′
新知引入
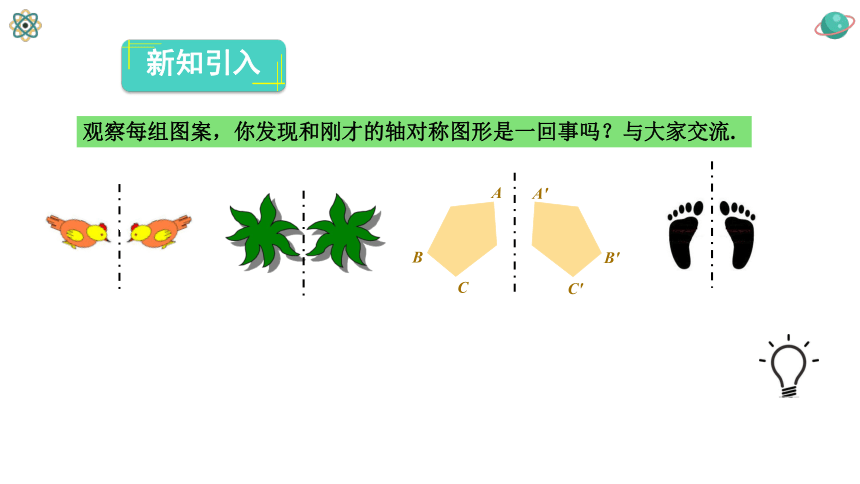
观察每组图案,你发现和刚才的轴对称图形是一回事吗?与大家交流.
A
B
C
A′
B′
C′
新知讲解
两个图形成轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
A
B
C
A′
B′
C′
两个图形成轴对称
2
新知讲解
思考:成轴对称的两个图形全等吗?如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
A
B
C
A′
B′
C′
新知讲解
轴对称图形 两个图形成轴对称
区别 一个图形的形状 两个图形的形状和位置
联 系 1.沿一条直线折叠,直线两旁的部分能够互相重合 (即直线两旁的两部分全等) 2.都有对称轴(至少一条) 3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线对称;如果把两个成轴对称的图形看成一个图形,那么这个图形就是轴对称图形.
新知应用
例3 想一想:一辆汽车的车牌在水中的倒影如图所示,
你能确定该车的车牌号码吗
新知应用
例4 如图,在2×3的正方形网络中,有一个以格点为顶点
的三角形,此网格中所有与该三角形成轴对称且以格点为
顶点的三角形共有( )
A.1个 B.2个 C.3个 D.4个
C
新知演练
【变式1】如图,ΔABC与ΔA′B′C′关于直线l对称,则∠B的度数为( )
A.30° B.50° C.90° D.100°
D
新知演练
【变式2】视力表中的字母“E”有各种不同的摆放形式,下面每种组合中的两个字母“E”不能关于某条直线成轴对称的是( )
A. B. C. D.
C
新知演练
【变式3】如图△ABC与△DEF关于直线MN成轴对称,那么线段AC的对应线段是( )
A.AB B.DF C.DE D.EF
B
新知讲解
探索成轴对称的两个图形的性质
如图,△ABC与△A′ B′ C′关于直线MN对称,点A′ , B′ , C′分别是点A,B,C的对称点,线段A A′ ,BB′ ,CC′与直线MN有什么关系?
A A′ 与直线MN垂直,
BB′ ,CC′也与直线MN垂直,
同时,直线MN 平分线段A A′ ,BB′ ,CC′ .
A
B
C
A′
B′
C′
M
N
P
轴对称的性质
3
新知讲解
∠MPA=∠MPA′=90°
AP=PA′
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
A
B
C
A′
B′
C′
M
N
P
新知讲解
A
B
C
A′
B′
C′
M
N
P
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
A
B
A′
B′
l
新知应用
例5 如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150° C.40° D.65°
A
新知应用
例6 如图,六边形ABCDEF是轴对称图形,所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是( )
A.150° B.300° C.210° D.330°
B
A
B
C
F
D
E
新知演练
【变式1】将矩形ABCD沿AE折叠,得到如图所示图形. 若∠CED′=56°,则∠AED的大小是_______.
62°
提示:∠AED=(180°-56°)÷2=62° .
新知演练
【变式2】如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
B
提示:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半,
∵正方形ABCD的边长为4cm,
∴S阴影=42÷2=8(cm2) .
拓展提升
1.如图,O为△ABC内部一点,OB= 3 ,P、R为O分别以直线AB、BC为对称轴的对称点.
(1)请指出当∠ABC是什么角度时,会使得PR的长度等于6?并完整说明PR的长度为何在此时等于 6的理由.
解:如图,∠ABC=90°时,PR=6.
证明如下:连接PB、RB,
∵P、R为O分别以直线AB、BC为对称轴
的对称点,
∴PB=OB=3,RB=OB=3.
∵∠ABC=90°,∴∠ABP+∠CBR=
∠ABO+∠CBO=∠ABC=90°,
∴∠PBR=180°,即P、B、R三点共线,
∴PR=PB+RB=3+3=6;
拓展提升
(2)承(1)小题,请判断当∠ABC不是你指出的角
度时,PR的长度小于6还是大于6?并完整说
明你判断的理由.
解:PR的长度小于6,理由如下:
∠ABC≠90°,则点P、B、R三点不在
同一直线上,∴PB+BR>PR.
∵PB+BR=2OB=2×3=6,
∴PR<6.
拓展提升
课堂总结
区别
联系
轴
对
称
与
轴
对
称
图
形
轴对称是指两个图形沿某条直线对折能够完全重合
两部分都完全重合
轴对称图形是指一个图形的两个部分沿某条直线对折能够完全重合
都有对称轴
都有对称点
任何一对对应点所连线段的垂直平分线
轴对称
新知引入
议一议:观察下列图片,说一说它们的共同特征.
新知引入
这些美丽的图片均来自生活,细心观察之后,你能发现这些图形有什么共同特征吗?用自己的语言描述一下.
新知讲解
如果一个图形沿一条直线折叠,两直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线即折痕所在的直线就是它的对称轴.
轴对称和轴对称图形
1
新知讲解
我们学过的图形中,你知道哪些图形是轴对称图形吗?
下面的图形是轴对称图形吗 如果是,你能指出它的对称轴吗
线段、角、等腰三角形、圆、正方形
新知应用
例1 图中四个图形中,从几何图形的性质考虑,哪一个与其它三个不同?请叙述你的理由.
A
B
C
D
B不是轴对称图形
新知应用
例2 下列图形是轴对称图形吗?各有几条对称轴?
4条
5条
6条
5条
新知引入
你能发现每组图形的共同点吗?
A
B
C
A′
B′
C′
新知引入
观察每组图案,你发现和刚才的轴对称图形是一回事吗?与大家交流.
A
B
C
A′
B′
C′
新知讲解
两个图形成轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
A
B
C
A′
B′
C′
两个图形成轴对称
2
新知讲解
思考:成轴对称的两个图形全等吗?如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
A
B
C
A′
B′
C′
新知讲解
轴对称图形 两个图形成轴对称
区别 一个图形的形状 两个图形的形状和位置
联 系 1.沿一条直线折叠,直线两旁的部分能够互相重合 (即直线两旁的两部分全等) 2.都有对称轴(至少一条) 3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线对称;如果把两个成轴对称的图形看成一个图形,那么这个图形就是轴对称图形.
新知应用
例3 想一想:一辆汽车的车牌在水中的倒影如图所示,
你能确定该车的车牌号码吗
新知应用
例4 如图,在2×3的正方形网络中,有一个以格点为顶点
的三角形,此网格中所有与该三角形成轴对称且以格点为
顶点的三角形共有( )
A.1个 B.2个 C.3个 D.4个
C
新知演练
【变式1】如图,ΔABC与ΔA′B′C′关于直线l对称,则∠B的度数为( )
A.30° B.50° C.90° D.100°
D
新知演练
【变式2】视力表中的字母“E”有各种不同的摆放形式,下面每种组合中的两个字母“E”不能关于某条直线成轴对称的是( )
A. B. C. D.
C
新知演练
【变式3】如图△ABC与△DEF关于直线MN成轴对称,那么线段AC的对应线段是( )
A.AB B.DF C.DE D.EF
B
新知讲解
探索成轴对称的两个图形的性质
如图,△ABC与△A′ B′ C′关于直线MN对称,点A′ , B′ , C′分别是点A,B,C的对称点,线段A A′ ,BB′ ,CC′与直线MN有什么关系?
A A′ 与直线MN垂直,
BB′ ,CC′也与直线MN垂直,
同时,直线MN 平分线段A A′ ,BB′ ,CC′ .
A
B
C
A′
B′
C′
M
N
P
轴对称的性质
3
新知讲解
∠MPA=∠MPA′=90°
AP=PA′
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
A
B
C
A′
B′
C′
M
N
P
新知讲解
A
B
C
A′
B′
C′
M
N
P
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
A
B
A′
B′
l
新知应用
例5 如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150° C.40° D.65°
A
新知应用
例6 如图,六边形ABCDEF是轴对称图形,所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是( )
A.150° B.300° C.210° D.330°
B
A
B
C
F
D
E
新知演练
【变式1】将矩形ABCD沿AE折叠,得到如图所示图形. 若∠CED′=56°,则∠AED的大小是_______.
62°
提示:∠AED=(180°-56°)÷2=62° .
新知演练
【变式2】如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
B
提示:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半,
∵正方形ABCD的边长为4cm,
∴S阴影=42÷2=8(cm2) .
拓展提升
1.如图,O为△ABC内部一点,OB= 3 ,P、R为O分别以直线AB、BC为对称轴的对称点.
(1)请指出当∠ABC是什么角度时,会使得PR的长度等于6?并完整说明PR的长度为何在此时等于 6的理由.
解:如图,∠ABC=90°时,PR=6.
证明如下:连接PB、RB,
∵P、R为O分别以直线AB、BC为对称轴
的对称点,
∴PB=OB=3,RB=OB=3.
∵∠ABC=90°,∴∠ABP+∠CBR=
∠ABO+∠CBO=∠ABC=90°,
∴∠PBR=180°,即P、B、R三点共线,
∴PR=PB+RB=3+3=6;
拓展提升
(2)承(1)小题,请判断当∠ABC不是你指出的角
度时,PR的长度小于6还是大于6?并完整说
明你判断的理由.
解:PR的长度小于6,理由如下:
∠ABC≠90°,则点P、B、R三点不在
同一直线上,∴PB+BR>PR.
∵PB+BR=2OB=2×3=6,
∴PR<6.
拓展提升
课堂总结
区别
联系
轴
对
称
与
轴
对
称
图
形
轴对称是指两个图形沿某条直线对折能够完全重合
两部分都完全重合
轴对称图形是指一个图形的两个部分沿某条直线对折能够完全重合
都有对称轴
都有对称点
任何一对对应点所连线段的垂直平分线
