人教版数学九年级上册同步练习 23.1 图形的旋转(两课时,word版含答案)
文档属性
| 名称 | 人教版数学九年级上册同步练习 23.1 图形的旋转(两课时,word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 236.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 21:44:27 | ||
图片预览



文档简介
23.1 图形的旋转
第1课时 认识图形的旋转
1.下列运动形式属于旋转的是(
)
A.在空中上升的氢气球
B.飞驰的火车
C.拧开水龙头
D.运动员掷出的标枪
2.
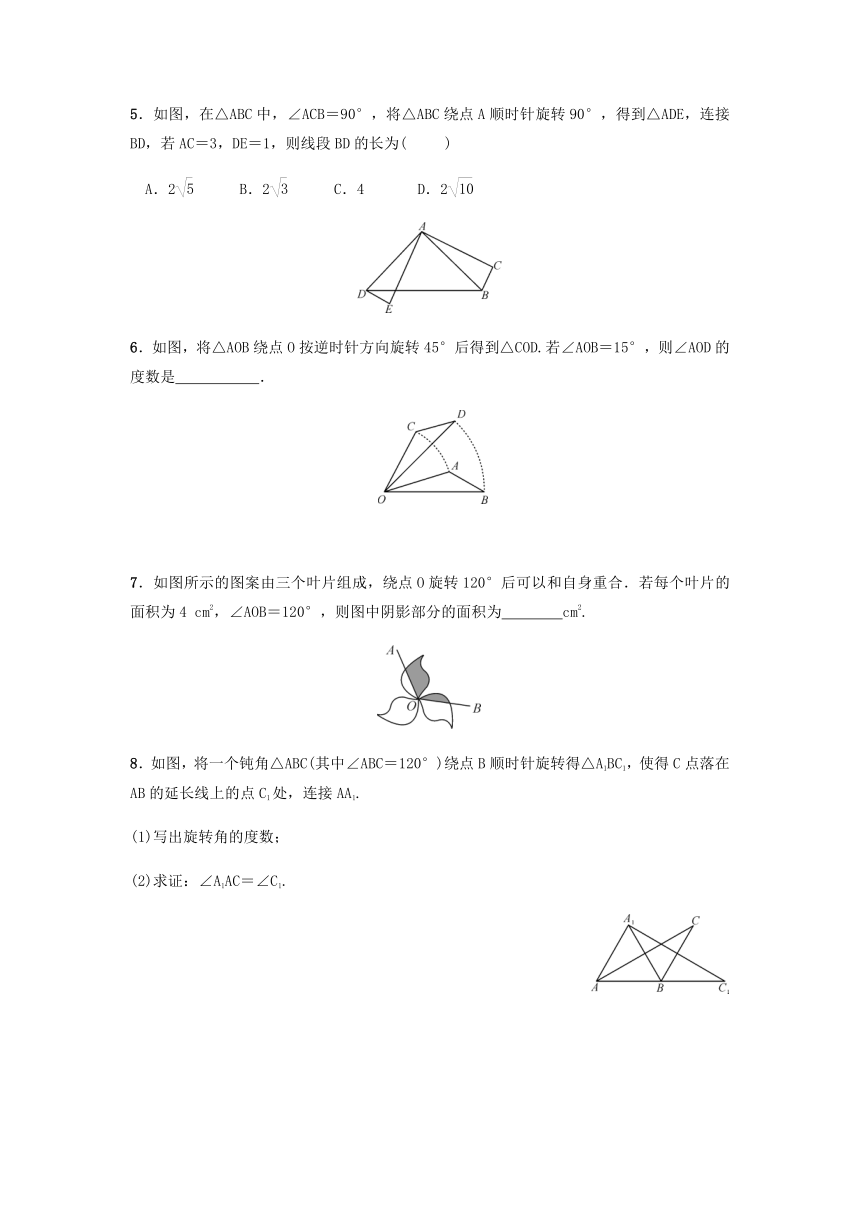
如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为(
)
3.下列图案中能由其中一个图形通过旋转而构成的有
.
4.如图,四边形ABCD是正方形,△ADE绕着点A旋转90°后到达△ABF的位置,连接EF,则△AEF的形状是(
)
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
5.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为(
)
A.2
B.2
C.4
D.2
6.如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD.若∠AOB=15°,则∠AOD的度数是
.
7.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4
cm2,∠AOB=120°,则图中阴影部分的面积为
cm2.
8.如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
9.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为(
)
A.35°
B.40°
C.50°
D.65°
10.如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则BD的长为(
)
A.0.5
B.1.5
D.1
11.如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°得到△OA1B1.
(1)线段A1B1的长是
,∠AOA1的度数是
;
(2)连接AA1,求证:四边形OAA1B1是平行四边形.
12.如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
13.(遵义名校联考)如图,将正方形ABCD绕顶点A顺时针旋转得到正方形AB′C′D′,Q是AB的中点,P是对角线B′D′的中点,连接PQ,若AB=2,则线段PQ的最小值是
.
第2课时 旋转作图
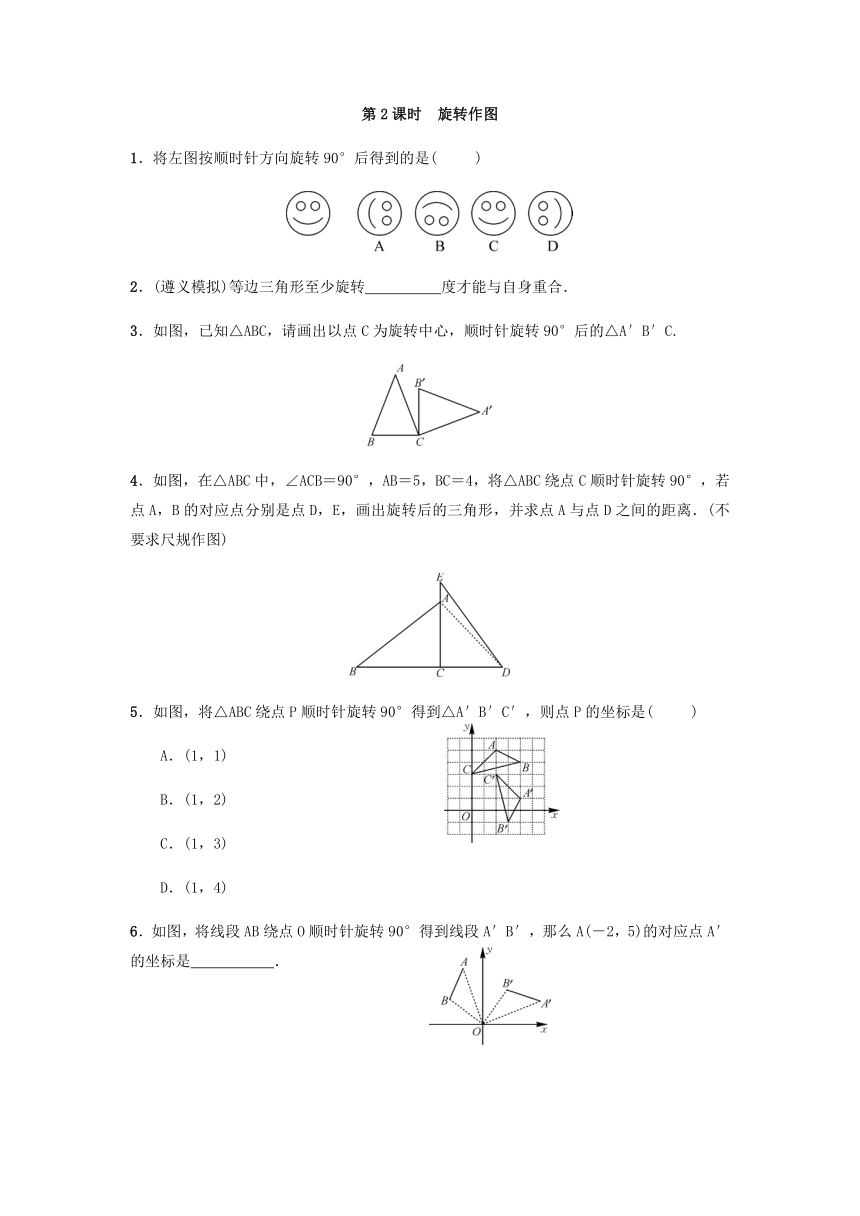
1.将左图按顺时针方向旋转90°后得到的是(
)
2.(遵义模拟)等边三角形至少旋转
度才能与自身重合.
3.如图,已知△ABC,请画出以点C为旋转中心,顺时针旋转90°后的△A′B′C.
4.如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
5.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是(
)
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
6.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是
.
7.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕原点O旋转180°后的△A2B2C2.
8.在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O旋转90°到OA′,则点A′的坐标是
.
9.
下列正多边形中,绕其中心旋转72°后,能和自身重合的是(
)
A.正方形
B.正五边形
C.正六边形
D.正八边形
10.如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为(
)
A.(2,2)
B.(-2,4)
C.(-2,2)
D.(-2,2)
11.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心一定是
.
12.如图,直线y=-x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A旋转90°后得到△AO′B′,则点B′的坐标是
.
13.如图,四边形ABCD绕点O旋转后,顶点A的对应点为点E,试确定B,C,D的对应点的位置并画出旋转后的四边形.
14.
如图,在平面直角坐标系中,点O为坐标原点,△AOB的顶点A,B的坐标分别为A(0,4),B(-3,0),按要求解答下列问题.
(1)在图中,先将△AOB向上平移6个单位长度,再向右平移3个单位长度,画出平移后的△A1O1B1;(其中点A,O,B的对应点分别为A1,O1,B1)
(2)在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1,B1的对应点分别为A2,B2)
(3)直接写出点A2,B2的坐标.
15.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
参考答案:
23.1 图形的旋转
第1课时 认识图形的旋转
1.C
2.
A
3.
①②.
4.C
5.A
6.
30°.
7.
4
.
8.解:(1)旋转角的度数为60°.
(2)证明:∵点A,B,C1在一条直线上,
∴∠ABC1=180°.
∵∠ABC=∠A1BC1=120°,
∴∠ABA1=∠CBC1=60°.
∴∠A1BC=60°.
又∵AB=A1B,∴△ABA1是等边三角形.
∴∠AA1B=∠A1BC=60°.
∴AA1∥BC.
∴∠A1AC=∠C.
∵△ABC≌△A1BC1,
∴∠C=∠C1.
∴∠A1AC=∠C1.
9.C
10.D
11.(1)
6,
90°;
(2)解:由旋转的性质,得A1B1=AB=6,OA1=OA=6,∠OA1B1=∠OAB=90°,∠AOA1=90°,
∴∠OA1B1=∠AOA1,A1B1=OA.
∴B1A1∥OA.
∴四边形OAA1B1是平行四边形.
12.解:(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM.
∴F,C,M三点共线.
∴DE=DM,∠EDM=90°.
∴∠EDF+∠FDM=90°.
∵∠EDF=45°,
∴∠FDM=∠EDF=45°.
在△DEF和△DMF中,
∵
∴△DEF≌△DMF(SAS).
∴EF=MF.
∴EF=CF+AE.
(2)设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8.
∴BF=BM-MF=BM-EF=8-x.
在Rt△EBF中,由勾股定理,得EB2+BF2=EF2,即42+(8-x)2=x2.
解得x=5.则EF=5.
-1.
第2课时 旋转作图
1.A
2.
120
.
3.
解:如图所示.
4.
解:如图,∵在△ABC中,∠ACB=90°,AB=5,BC=4,
∴AC==3.
∵将△ABC绕点C顺时针旋转90°,点A,B的对应点分别是点D,E,
∴AC=CD=3,∠ACD=90°.
∴AD==3.
5.B
6.
(5,2).
7.
解:(1)如图,△A1B1C1为所作.
(2)如图,△A2B2C2为所作.
8.
(-4,3)或(4,-3).
9.
B
10.D
11.
点B.
12.
(-1,-2)或(5,2).
13.
解:如图,B,C,D的对应点分别是F,G,H,四边形EFGH是四边形ABCD绕点O旋转后得到的四边形.
14.
解:(1)如图,△A1O1B1为所作.
(2)如图,Rt△A2O1B2为所作.
(3)点A2,B2的坐标分别为(7,6),(3,9).
15.
解:(1)△A1B1C如图所示,△A2B2C2如图所示.
(2)旋转中心坐标为(1.5,3).
(3)如图所示,点P的坐标为(-2,0).
第1课时 认识图形的旋转
1.下列运动形式属于旋转的是(
)
A.在空中上升的氢气球
B.飞驰的火车
C.拧开水龙头
D.运动员掷出的标枪
2.
如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为(
)
3.下列图案中能由其中一个图形通过旋转而构成的有
.
4.如图,四边形ABCD是正方形,△ADE绕着点A旋转90°后到达△ABF的位置,连接EF,则△AEF的形状是(
)
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
5.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为(
)
A.2
B.2
C.4
D.2
6.如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD.若∠AOB=15°,则∠AOD的度数是
.
7.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4
cm2,∠AOB=120°,则图中阴影部分的面积为
cm2.
8.如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
9.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为(
)
A.35°
B.40°
C.50°
D.65°
10.如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则BD的长为(
)
A.0.5
B.1.5
D.1
11.如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°得到△OA1B1.
(1)线段A1B1的长是
,∠AOA1的度数是
;
(2)连接AA1,求证:四边形OAA1B1是平行四边形.
12.如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
13.(遵义名校联考)如图,将正方形ABCD绕顶点A顺时针旋转得到正方形AB′C′D′,Q是AB的中点,P是对角线B′D′的中点,连接PQ,若AB=2,则线段PQ的最小值是
.
第2课时 旋转作图
1.将左图按顺时针方向旋转90°后得到的是(
)
2.(遵义模拟)等边三角形至少旋转
度才能与自身重合.
3.如图,已知△ABC,请画出以点C为旋转中心,顺时针旋转90°后的△A′B′C.
4.如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
5.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是(
)
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
6.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是
.
7.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕原点O旋转180°后的△A2B2C2.
8.在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O旋转90°到OA′,则点A′的坐标是
.
9.
下列正多边形中,绕其中心旋转72°后,能和自身重合的是(
)
A.正方形
B.正五边形
C.正六边形
D.正八边形
10.如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为(
)
A.(2,2)
B.(-2,4)
C.(-2,2)
D.(-2,2)
11.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心一定是
.
12.如图,直线y=-x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A旋转90°后得到△AO′B′,则点B′的坐标是
.
13.如图,四边形ABCD绕点O旋转后,顶点A的对应点为点E,试确定B,C,D的对应点的位置并画出旋转后的四边形.
14.
如图,在平面直角坐标系中,点O为坐标原点,△AOB的顶点A,B的坐标分别为A(0,4),B(-3,0),按要求解答下列问题.
(1)在图中,先将△AOB向上平移6个单位长度,再向右平移3个单位长度,画出平移后的△A1O1B1;(其中点A,O,B的对应点分别为A1,O1,B1)
(2)在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1,B1的对应点分别为A2,B2)
(3)直接写出点A2,B2的坐标.
15.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
参考答案:
23.1 图形的旋转
第1课时 认识图形的旋转
1.C
2.
A
3.
①②.
4.C
5.A
6.
30°.
7.
4
.
8.解:(1)旋转角的度数为60°.
(2)证明:∵点A,B,C1在一条直线上,
∴∠ABC1=180°.
∵∠ABC=∠A1BC1=120°,
∴∠ABA1=∠CBC1=60°.
∴∠A1BC=60°.
又∵AB=A1B,∴△ABA1是等边三角形.
∴∠AA1B=∠A1BC=60°.
∴AA1∥BC.
∴∠A1AC=∠C.
∵△ABC≌△A1BC1,
∴∠C=∠C1.
∴∠A1AC=∠C1.
9.C
10.D
11.(1)
6,
90°;
(2)解:由旋转的性质,得A1B1=AB=6,OA1=OA=6,∠OA1B1=∠OAB=90°,∠AOA1=90°,
∴∠OA1B1=∠AOA1,A1B1=OA.
∴B1A1∥OA.
∴四边形OAA1B1是平行四边形.
12.解:(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM.
∴F,C,M三点共线.
∴DE=DM,∠EDM=90°.
∴∠EDF+∠FDM=90°.
∵∠EDF=45°,
∴∠FDM=∠EDF=45°.
在△DEF和△DMF中,
∵
∴△DEF≌△DMF(SAS).
∴EF=MF.
∴EF=CF+AE.
(2)设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8.
∴BF=BM-MF=BM-EF=8-x.
在Rt△EBF中,由勾股定理,得EB2+BF2=EF2,即42+(8-x)2=x2.
解得x=5.则EF=5.
-1.
第2课时 旋转作图
1.A
2.
120
.
3.
解:如图所示.
4.
解:如图,∵在△ABC中,∠ACB=90°,AB=5,BC=4,
∴AC==3.
∵将△ABC绕点C顺时针旋转90°,点A,B的对应点分别是点D,E,
∴AC=CD=3,∠ACD=90°.
∴AD==3.
5.B
6.
(5,2).
7.
解:(1)如图,△A1B1C1为所作.
(2)如图,△A2B2C2为所作.
8.
(-4,3)或(4,-3).
9.
B
10.D
11.
点B.
12.
(-1,-2)或(5,2).
13.
解:如图,B,C,D的对应点分别是F,G,H,四边形EFGH是四边形ABCD绕点O旋转后得到的四边形.
14.
解:(1)如图,△A1O1B1为所作.
(2)如图,Rt△A2O1B2为所作.
(3)点A2,B2的坐标分别为(7,6),(3,9).
15.
解:(1)△A1B1C如图所示,△A2B2C2如图所示.
(2)旋转中心坐标为(1.5,3).
(3)如图所示,点P的坐标为(-2,0).
同课章节目录
