4.4一次函数的应用-北师大版八年级数学上册假期同步测试(Word版 含答案)
文档属性
| 名称 | 4.4一次函数的应用-北师大版八年级数学上册假期同步测试(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 00:00:00 | ||
图片预览


文档简介
北师大版八年级数学上册第四章4.4一次函数的应用
同步测试
一、选择题
1.(2020?嘉兴)一次函数y=2x﹣1的图象大致是( )
A.B.
C.
D.
2.(2020?内江)将直线y=﹣2x﹣1向上平移两个单位,平移后的直线所对应的函数关系式为( )
A.y=﹣2x﹣5
B.y=﹣2x﹣3
C.y=﹣2x+1
D.y=﹣2x+3
3.方程2x+12=0的解是直线y=2x+12( )
A.与y轴交点的横坐标
B.与y轴交点的纵坐标
C.与x轴交点的横坐标
D.与x轴交点的纵坐标
4.若正比例函数y=﹣2x的图象经过点O(a﹣1,4),则a的值为( )
A.﹣1
B.0
C.1
D.2
5.如图,反映了某公司的销售收入与销售量的关系,反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量(
)
A.小于3
t
B.大于3
t
C.小于4
t
D.大于4
t
6.如果函数y=kx+b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是( )
A.k≥0且b≤0
B.k>0且b≤0
C.k≥0且b<0
D.k>0且b<0
7.若直线y=-x+a与直线y=x+b的交点坐标为(m,6),则2(a+b)的结果为( )
A.8
B.16
C.24
D.32
8.(2020?安徽)已知一次函数y=kx+3的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )
A.(﹣1,2)
B.(1,﹣2)
C.(2,3)
D.(3,4)
9.在同一平面直角坐标系中,若一次函数y=-x+1与y=2x+4的图象交于点M,则点M的坐标为( )
A.(-1,-2)
B.(-1,2)
C.(2,1)
D.(-2,1)
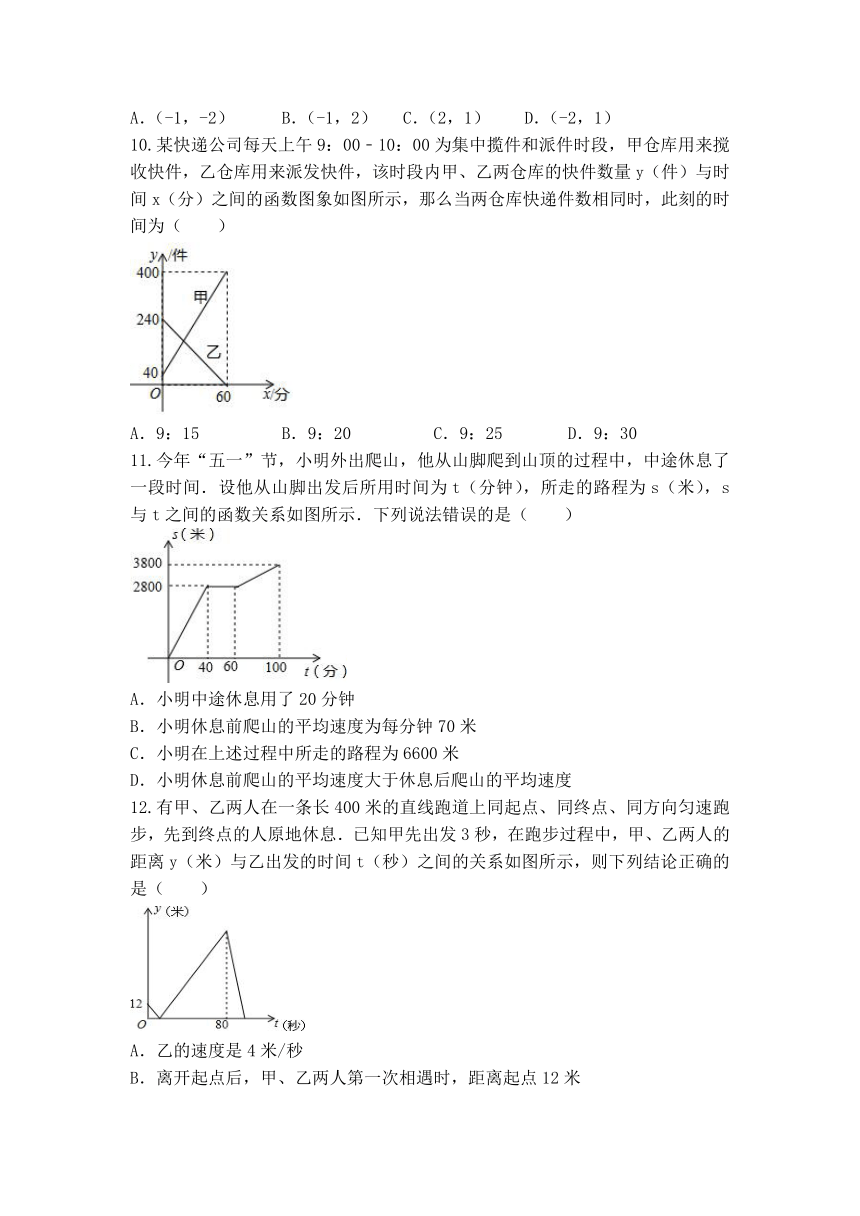
10.某快递公司每天上午9:00﹣10:00为集中揽件和派件时段,甲仓库用来搅收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.9:15
B.9:20
C.9:25
D.9:30
11.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
12.有甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的是( )
A.乙的速度是4米/秒
B.离开起点后,甲、乙两人第一次相遇时,距离起点12米
C.甲从起点到终点共用时83秒
D.乙到达终点时,甲、乙两人相距68米
二、填空题
13.已知直线y=kx+b与x轴的交点坐标是(2,0),则关于x的方程kx+b=0的解是x=
14.若正比例函数y=kx(k≠0),点(2,-3)在函数上,则随的增大
而
(增大或减小)
15.已知关于x的一元一次方程kx+b=0的解是x=-2,一次函数y=kx+b的图象与y轴交于点(0,2),则这个一次函数的表达式是
16.如图,射线OA,BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中,分别表示行驶距离和时间,则这两人骑自行车的速度相差
km/h.
17.(2020?临沂)点(,m)和点(2,n)在直线y=2x+b上,则m与n的大小关系是
.
18.直线y=kx+b与直线y=-3x+2平行,且经过点(1,6),则该函数关系式为
?
19.某食品厂向A市销售面包,如果从铁路托运,每千克需运费0.58元;如果从公路托运,每千克需运费0.28元,另需出差补助600元。(1)设该市向A市销售面包x千克,铁路运费y1元,公路运费y2元,则y1,y2与x之间的函数关系式分别为_______,_________;
(2)若厂家只出运费1500元,选用______运送,运送面包多;
(3)若厂家运送1500千克,选用______运送,所需运费少.
20.(2020?重庆)A,B两地相距240km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止.在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止.两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.其中点C的坐标是(0,240),点D的坐标是(2.4,0),则点E的坐标是
.
三.解答题
21.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(1)方程kx+b=0的解;
(2)式子k+b的值;
(3)方程kx+b=-3的解.
22.今年端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时的路程(米)与时间(分)之间的函数图象如图所示.请你根据图象回答下列问题:
(1)1.8分时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?提前多少时间到达?
23.在平面直角坐标系xOy中(如图),已知一次函数的图象平行于直线y=x,且经过点A(2,3),与x轴交于点B.
(1)求这个一次函数的解析式;
(2)设点C在y轴上,当AC=BC时,求点C的坐标.
24.(2020?陕西)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式;
(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?
答案提示
1.B.2.C.3.C.4.A.
5.D
6.A.
7.C.8.B.
9.B.
10.B.11.C.12.D.
13.
2.
14.减小
15.y=-x+2.
16.4
17.m<n.
18.y=-3x+9
19.(1),(2)铁路(3)公路
20.(4,160).
21.答案:(1)x=2;(2)-1(3)-1
解:(1)如图所示,当y=0时,x=2.
故方程kx+b=0的解是x=2;
(2)根据图示知,该直线经过点(2,0)和点(0,-2),则,
解得,
故k+b=1-2=-1,即k+b=-1;
(3)根据图示知,当y=-3时,x=-1.
故方程kx+b=-3的解是x=-1.
22.
解:(1)1.8分时,甲龙舟队处于领先位置
(2)在这次龙舟赛中,乙龙舟队先到达终点,提前0.5分到达
23.
解:(1)设一次函数的解析式为:y=kx+b,
∵一次函数的图象平行于直线y=x,
∴k=,
∵一次函数的图象经过点A(2,3),
∴3=+b,
∴b=2,
∴一次函数的解析式为y=x+2;
(2)由y=x+2,令y=0,得x+2=0,
∴x=﹣4,
∴一次函数的图形与x轴的解得为B(﹣4,0),
∵点C在y轴上,
∴设点C的坐标为(0,y),
∵AC=BC,
∴=,
∴y=﹣,
经检验:y=﹣是原方程的根,
∴点C的坐标是(0,﹣).
24.
解:(1)当0≤x≤15时,设y=kx(k≠0),
则:20=15k,
解得k,
∴y;
当15<x≤60时,设y=k′x+b(k≠0),
则:,
解得,
∴y,
∴;
(2)当y=80时,80,解得x=33,
33﹣15=18(天),
∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.
同步测试
一、选择题
1.(2020?嘉兴)一次函数y=2x﹣1的图象大致是( )
A.B.
C.
D.
2.(2020?内江)将直线y=﹣2x﹣1向上平移两个单位,平移后的直线所对应的函数关系式为( )
A.y=﹣2x﹣5
B.y=﹣2x﹣3
C.y=﹣2x+1
D.y=﹣2x+3
3.方程2x+12=0的解是直线y=2x+12( )
A.与y轴交点的横坐标
B.与y轴交点的纵坐标
C.与x轴交点的横坐标
D.与x轴交点的纵坐标
4.若正比例函数y=﹣2x的图象经过点O(a﹣1,4),则a的值为( )
A.﹣1
B.0
C.1
D.2
5.如图,反映了某公司的销售收入与销售量的关系,反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量(
)
A.小于3
t
B.大于3
t
C.小于4
t
D.大于4
t
6.如果函数y=kx+b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是( )
A.k≥0且b≤0
B.k>0且b≤0
C.k≥0且b<0
D.k>0且b<0
7.若直线y=-x+a与直线y=x+b的交点坐标为(m,6),则2(a+b)的结果为( )
A.8
B.16
C.24
D.32
8.(2020?安徽)已知一次函数y=kx+3的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )
A.(﹣1,2)
B.(1,﹣2)
C.(2,3)
D.(3,4)
9.在同一平面直角坐标系中,若一次函数y=-x+1与y=2x+4的图象交于点M,则点M的坐标为( )
A.(-1,-2)
B.(-1,2)
C.(2,1)
D.(-2,1)
10.某快递公司每天上午9:00﹣10:00为集中揽件和派件时段,甲仓库用来搅收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.9:15
B.9:20
C.9:25
D.9:30
11.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
12.有甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的是( )
A.乙的速度是4米/秒
B.离开起点后,甲、乙两人第一次相遇时,距离起点12米
C.甲从起点到终点共用时83秒
D.乙到达终点时,甲、乙两人相距68米
二、填空题
13.已知直线y=kx+b与x轴的交点坐标是(2,0),则关于x的方程kx+b=0的解是x=
14.若正比例函数y=kx(k≠0),点(2,-3)在函数上,则随的增大
而
(增大或减小)
15.已知关于x的一元一次方程kx+b=0的解是x=-2,一次函数y=kx+b的图象与y轴交于点(0,2),则这个一次函数的表达式是
16.如图,射线OA,BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中,分别表示行驶距离和时间,则这两人骑自行车的速度相差
km/h.
17.(2020?临沂)点(,m)和点(2,n)在直线y=2x+b上,则m与n的大小关系是
.
18.直线y=kx+b与直线y=-3x+2平行,且经过点(1,6),则该函数关系式为
?
19.某食品厂向A市销售面包,如果从铁路托运,每千克需运费0.58元;如果从公路托运,每千克需运费0.28元,另需出差补助600元。(1)设该市向A市销售面包x千克,铁路运费y1元,公路运费y2元,则y1,y2与x之间的函数关系式分别为_______,_________;
(2)若厂家只出运费1500元,选用______运送,运送面包多;
(3)若厂家运送1500千克,选用______运送,所需运费少.
20.(2020?重庆)A,B两地相距240km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止.在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止.两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.其中点C的坐标是(0,240),点D的坐标是(2.4,0),则点E的坐标是
.
三.解答题
21.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(1)方程kx+b=0的解;
(2)式子k+b的值;
(3)方程kx+b=-3的解.
22.今年端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时的路程(米)与时间(分)之间的函数图象如图所示.请你根据图象回答下列问题:
(1)1.8分时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?提前多少时间到达?
23.在平面直角坐标系xOy中(如图),已知一次函数的图象平行于直线y=x,且经过点A(2,3),与x轴交于点B.
(1)求这个一次函数的解析式;
(2)设点C在y轴上,当AC=BC时,求点C的坐标.
24.(2020?陕西)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.
(1)求y与x之间的函数关系式;
(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?
答案提示
1.B.2.C.3.C.4.A.
5.D
6.A.
7.C.8.B.
9.B.
10.B.11.C.12.D.
13.
2.
14.减小
15.y=-x+2.
16.4
17.m<n.
18.y=-3x+9
19.(1),(2)铁路(3)公路
20.(4,160).
21.答案:(1)x=2;(2)-1(3)-1
解:(1)如图所示,当y=0时,x=2.
故方程kx+b=0的解是x=2;
(2)根据图示知,该直线经过点(2,0)和点(0,-2),则,
解得,
故k+b=1-2=-1,即k+b=-1;
(3)根据图示知,当y=-3时,x=-1.
故方程kx+b=-3的解是x=-1.
22.
解:(1)1.8分时,甲龙舟队处于领先位置
(2)在这次龙舟赛中,乙龙舟队先到达终点,提前0.5分到达
23.
解:(1)设一次函数的解析式为:y=kx+b,
∵一次函数的图象平行于直线y=x,
∴k=,
∵一次函数的图象经过点A(2,3),
∴3=+b,
∴b=2,
∴一次函数的解析式为y=x+2;
(2)由y=x+2,令y=0,得x+2=0,
∴x=﹣4,
∴一次函数的图形与x轴的解得为B(﹣4,0),
∵点C在y轴上,
∴设点C的坐标为(0,y),
∵AC=BC,
∴=,
∴y=﹣,
经检验:y=﹣是原方程的根,
∴点C的坐标是(0,﹣).
24.
解:(1)当0≤x≤15时,设y=kx(k≠0),
则:20=15k,
解得k,
∴y;
当15<x≤60时,设y=k′x+b(k≠0),
则:,
解得,
∴y,
∴;
(2)当y=80时,80,解得x=33,
33﹣15=18(天),
∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
