北师大版数学九年级下册 3.2 圆的对称性 课件(32张ppt)
文档属性
| 名称 | 北师大版数学九年级下册 3.2 圆的对称性 课件(32张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 00:00:00 | ||
图片预览









文档简介
第三章 圆
第2节 圆的对称性
1
课堂讲解
圆的对称性
圆心角与所对的弧、弦之间的关系
相等圆心角、弧、弦之间的关系
2
课时流程
逐点
导讲练
课堂小结
作业提升
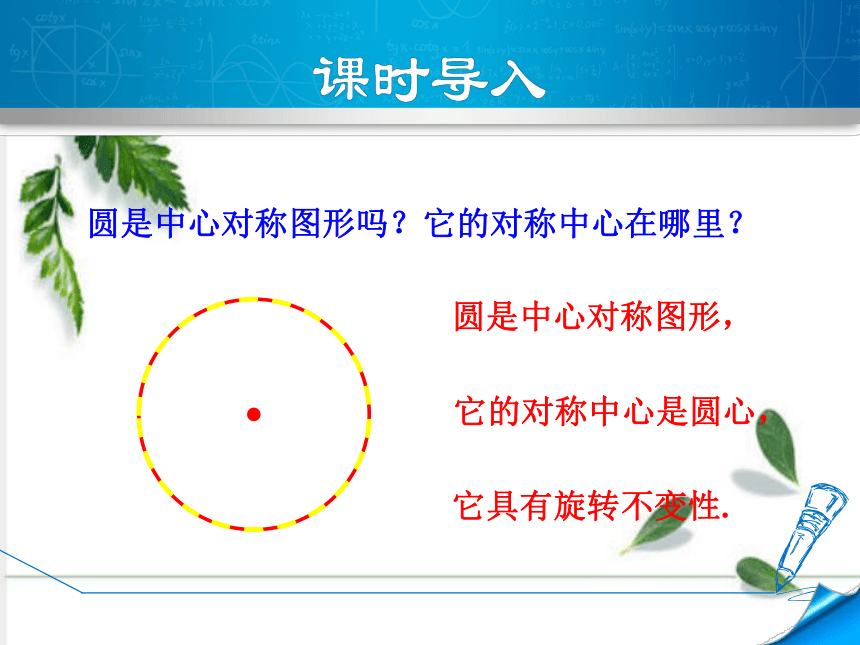
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
1
知识点
圆的对称性
1.一个圆绕着它的圆心旋转任意一个角度,都能与原来
的图形重合,这就是圆的旋转不变性.
2.把圆绕圆心旋转180°,所得的图形与原图形重合,
所以圆是中心对称图形,对称中心为圆心.
知1-讲
知1-讲
下列命题中,正确的是( )
A. 圆和正方形都既是轴对称图形,又是中心对称图形
B. 圆和正方形的对称轴都有无数条
C. 圆和正方形绕其对称中心旋转任意
例1
导引:
紧扣圆和正方形的轴对称性及中心对称性进行辨析.
解:圆和正方形都既是轴对称图形,又是中心对称图形,所以A 中命题正确;圆的对称轴有无数条,正方形的对称轴有4 条,所以B,D 中命题错误;圆绕其对称中心旋转任意一个角度都能与原来的图形重合,而正方形只有绕它的对称中心旋转90°或90°的整数倍才能与原图形重合,所以C 中命题错误. 故选A.
A
总 结
知1-讲
1. 圆有无数条对称轴,但只有一个对称中心.
2. 因为直径是弦,弦是线段,而对称轴是直线,所以说“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线”.
知1-练
日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
1
解:略.
知1-练
利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1) 是轴对称图形但不是中心对称图形;
(2) 是中心对称图形但不是轴对称图形;
(3) 既是轴对称图形又是中心对称图形.
2
解: (1)如图①②是轴对称图形但不是中心对称图形;
(2)如图③是中心对称图形但不是轴对称图形;
(3)如图④既是轴对称图形又是中心对称图形.
知1-练
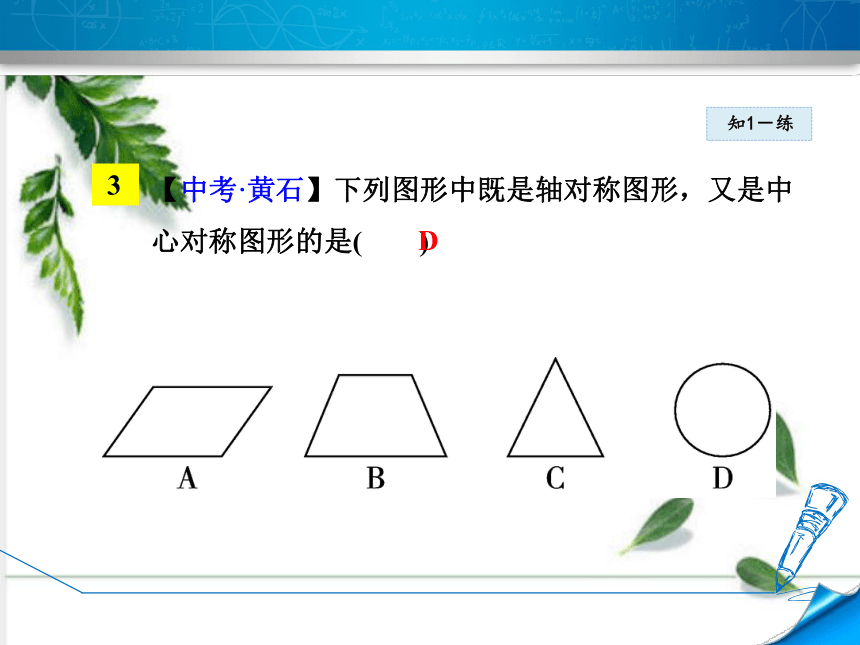
【中考·黄石】下列图形中既是轴对称图形,又是中心对称图形的是( )
3
D
知2-导
在同圆或等圆中,如果两个圆心角所对的弧相等,那
么它们所对的弦相等 吗?这两个圆心角相等吗?你是怎
么想的?
在同圆或等圆中,如果两条弦相等,你能得出什么
结论?
2
知识点
圆心角与所对的弧、弦之间的关系
归 纳
知2-导
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
知2-讲
例2如图所示,AB,CD 是⊙ O 的两条直径,弦CE ∥ AB,求证:?BC =?AE .
知2-讲
导引:
如图所示,连接OE.
∵ OE=OC,
∴∠ C= ∠ E.
∵ CE ∥ AB,
∴∠ C= ∠ BOC,∠ E= ∠ AOE.
∴∠ BOC= ∠ AOE.
∴?BC = ?AE .
总 结
知2-讲
由 结论可知,在同圆中,圆的两条平行弦所夹的弧相等.
知2-练
下面四个图形中的角,是圆心角的是( )
1
D
知2-练
如图,AB为⊙O的弦,∠A=40°,则AB所对的圆心角等于( )
A.40°
B.80°
C.100°
D.120°
2
︵
C
知2-练
如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则BD的度数为( )
A.25°
B.30°
C.50°
D.65°
3
︵
C
知2-练
【中考·台湾】如图,圆O过五边形OABCD的四个顶点.若AD=150°,∠A=65°,∠D=60°,则BC的度数为何?( )
A.25°
B.40°
C.50°
D.55°
4
︵
︵
B
知2-练
已知AB,CD是⊙O的直径,弦CE∥AB,∠COE=40°,则BD的度数是( )
A.70° B.110°
C.40° D.70°或110°
5
︵
D
3
知识点
相等圆心角、弧、弦之间的关系
知3-导
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的
位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
知3-导
如图,⊙O与⊙O1是等圆,∠AOB =∠A1OB1=60°,请问上述结论还成立吗?为什么?
·
O
A
B
A1
·
O1
B1
·
知3-导
归 纳
弧、弦、圆心角之间的关系.
在同圆或等圆中:
(1)相等的圆心角所对的弧相等,所对的弦也相等.
(2)相等的弧所对的圆心角相等,所对的弦也相等.
(3)相等的弦所对的圆心角相等,所对的弧也相等.
知3-讲
如图, AB,DE是⊙O的直径,C是⊙O上的一点,且
. BE与CE的大小有什么关系?为什么?
例3
解:
BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.
知3-练
已知A,B是⊙O上的两点,∠AOB= 120°,C是AB的中点. 试确定四边形 OACB的形状,并说明理由.
1
如图,四边形OACB是菱形.理由如下:连接OC.
∵C是AB的中点,
∴AC=BC. ∴∠AOC=∠BOC.
∵∠AOB=120°,∴∠AOC=∠BOC=60°.
又∵OB=OC,OA=OC,
∴△BOC和△AOC都是等边三角形.
∴OB=BC=CA=AO. ∴四边形OACB是菱形.
解:
︵
︵
︵
︵
知3-练
如图,AB是⊙O的直径,若∠COA=∠DOB=60°,则与线段AO的长度相等的线段有( )
A.3条
B.4条
C.5条
D.6条
2
D
知3-练
在⊙O中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
A. AB=2CD
B. AB>2CD
C. AB<2CD
D.不能确定
3
︵
︵
︵
︵
︵
︵
︵
︵
A
知3-练
在⊙O中,M,N分别为弦AB,CD的中点,如果OM=ON,那么在结论:①AB=CD;②AB=CD;③∠AOB=∠COD中,正确的是( )
A.①② B.①③
C.②③ D.①②③
4
︵
︵
D
知3-练
【中考·兰州】如图,在⊙O中,点C是AB的中点,∠A=50°,则∠BOC等于( )
A.40°
B.45°
C.50°
D.60°
5
︵
A
1. 圆的中心对称性:圆是中心对称图形,具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
1
知识小结
如图,在⊙O中,弦AB>CD,OM⊥AB,ON⊥CD,M,N分别为垂足,那么OM,ON的大小关系是( )
A.OM>ON
B.OM=ON
C.OMD.无法确定
易错点:对圆中的有关线段的关系运用不当而致错
2
易错小结
C
A或B
对于“在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都相等”这一性质中反映的各组量之间的关系判断不准,从而导致错误.
错解:
诊断:
谢谢!
第2节 圆的对称性
1
课堂讲解
圆的对称性
圆心角与所对的弧、弦之间的关系
相等圆心角、弧、弦之间的关系
2
课时流程
逐点
导讲练
课堂小结
作业提升
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
1
知识点
圆的对称性
1.一个圆绕着它的圆心旋转任意一个角度,都能与原来
的图形重合,这就是圆的旋转不变性.
2.把圆绕圆心旋转180°,所得的图形与原图形重合,
所以圆是中心对称图形,对称中心为圆心.
知1-讲
知1-讲
下列命题中,正确的是( )
A. 圆和正方形都既是轴对称图形,又是中心对称图形
B. 圆和正方形的对称轴都有无数条
C. 圆和正方形绕其对称中心旋转任意
例1
导引:
紧扣圆和正方形的轴对称性及中心对称性进行辨析.
解:圆和正方形都既是轴对称图形,又是中心对称图形,所以A 中命题正确;圆的对称轴有无数条,正方形的对称轴有4 条,所以B,D 中命题错误;圆绕其对称中心旋转任意一个角度都能与原来的图形重合,而正方形只有绕它的对称中心旋转90°或90°的整数倍才能与原图形重合,所以C 中命题错误. 故选A.
A
总 结
知1-讲
1. 圆有无数条对称轴,但只有一个对称中心.
2. 因为直径是弦,弦是线段,而对称轴是直线,所以说“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线”.
知1-练
日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
1
解:略.
知1-练
利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1) 是轴对称图形但不是中心对称图形;
(2) 是中心对称图形但不是轴对称图形;
(3) 既是轴对称图形又是中心对称图形.
2
解: (1)如图①②是轴对称图形但不是中心对称图形;
(2)如图③是中心对称图形但不是轴对称图形;
(3)如图④既是轴对称图形又是中心对称图形.
知1-练
【中考·黄石】下列图形中既是轴对称图形,又是中心对称图形的是( )
3
D
知2-导
在同圆或等圆中,如果两个圆心角所对的弧相等,那
么它们所对的弦相等 吗?这两个圆心角相等吗?你是怎
么想的?
在同圆或等圆中,如果两条弦相等,你能得出什么
结论?
2
知识点
圆心角与所对的弧、弦之间的关系
归 纳
知2-导
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
知2-讲
例2如图所示,AB,CD 是⊙ O 的两条直径,弦CE ∥ AB,求证:?BC =?AE .
知2-讲
导引:
如图所示,连接OE.
∵ OE=OC,
∴∠ C= ∠ E.
∵ CE ∥ AB,
∴∠ C= ∠ BOC,∠ E= ∠ AOE.
∴∠ BOC= ∠ AOE.
∴?BC = ?AE .
总 结
知2-讲
由 结论可知,在同圆中,圆的两条平行弦所夹的弧相等.
知2-练
下面四个图形中的角,是圆心角的是( )
1
D
知2-练
如图,AB为⊙O的弦,∠A=40°,则AB所对的圆心角等于( )
A.40°
B.80°
C.100°
D.120°
2
︵
C
知2-练
如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则BD的度数为( )
A.25°
B.30°
C.50°
D.65°
3
︵
C
知2-练
【中考·台湾】如图,圆O过五边形OABCD的四个顶点.若AD=150°,∠A=65°,∠D=60°,则BC的度数为何?( )
A.25°
B.40°
C.50°
D.55°
4
︵
︵
B
知2-练
已知AB,CD是⊙O的直径,弦CE∥AB,∠COE=40°,则BD的度数是( )
A.70° B.110°
C.40° D.70°或110°
5
︵
D
3
知识点
相等圆心角、弧、弦之间的关系
知3-导
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的
位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
知3-导
如图,⊙O与⊙O1是等圆,∠AOB =∠A1OB1=60°,请问上述结论还成立吗?为什么?
·
O
A
B
A1
·
O1
B1
·
知3-导
归 纳
弧、弦、圆心角之间的关系.
在同圆或等圆中:
(1)相等的圆心角所对的弧相等,所对的弦也相等.
(2)相等的弧所对的圆心角相等,所对的弦也相等.
(3)相等的弦所对的圆心角相等,所对的弧也相等.
知3-讲
如图, AB,DE是⊙O的直径,C是⊙O上的一点,且
. BE与CE的大小有什么关系?为什么?
例3
解:
BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.
知3-练
已知A,B是⊙O上的两点,∠AOB= 120°,C是AB的中点. 试确定四边形 OACB的形状,并说明理由.
1
如图,四边形OACB是菱形.理由如下:连接OC.
∵C是AB的中点,
∴AC=BC. ∴∠AOC=∠BOC.
∵∠AOB=120°,∴∠AOC=∠BOC=60°.
又∵OB=OC,OA=OC,
∴△BOC和△AOC都是等边三角形.
∴OB=BC=CA=AO. ∴四边形OACB是菱形.
解:
︵
︵
︵
︵
知3-练
如图,AB是⊙O的直径,若∠COA=∠DOB=60°,则与线段AO的长度相等的线段有( )
A.3条
B.4条
C.5条
D.6条
2
D
知3-练
在⊙O中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
A. AB=2CD
B. AB>2CD
C. AB<2CD
D.不能确定
3
︵
︵
︵
︵
︵
︵
︵
︵
A
知3-练
在⊙O中,M,N分别为弦AB,CD的中点,如果OM=ON,那么在结论:①AB=CD;②AB=CD;③∠AOB=∠COD中,正确的是( )
A.①② B.①③
C.②③ D.①②③
4
︵
︵
D
知3-练
【中考·兰州】如图,在⊙O中,点C是AB的中点,∠A=50°,则∠BOC等于( )
A.40°
B.45°
C.50°
D.60°
5
︵
A
1. 圆的中心对称性:圆是中心对称图形,具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
1
知识小结
如图,在⊙O中,弦AB>CD,OM⊥AB,ON⊥CD,M,N分别为垂足,那么OM,ON的大小关系是( )
A.OM>ON
B.OM=ON
C.OM
易错点:对圆中的有关线段的关系运用不当而致错
2
易错小结
C
A或B
对于“在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都相等”这一性质中反映的各组量之间的关系判断不准,从而导致错误.
错解:
诊断:
谢谢!
