北师大版数学九年级下册 3.7 切线长定理 课件(25张ppt)
文档属性
| 名称 | 北师大版数学九年级下册 3.7 切线长定理 课件(25张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 23:24:02 | ||
图片预览




文档简介
第三章 圆
第7节 切线长定理
1
课堂讲解
切线长定理
2
课时流程
逐点
导讲练
课堂小结
作业提升
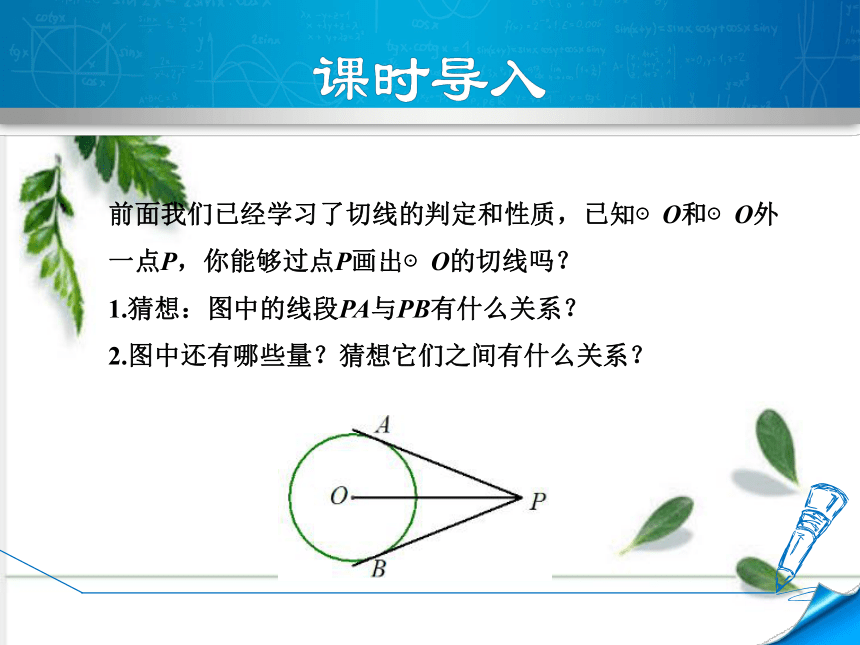
前面我们已经学习了切线的判定和性质,已知⊙O和⊙O外一点P,你能够过点P画出⊙O的切线吗?
1.猜想:图中的线段PA与PB有什么关系?
2.图中还有哪些量?猜想它们之间有什么关系?
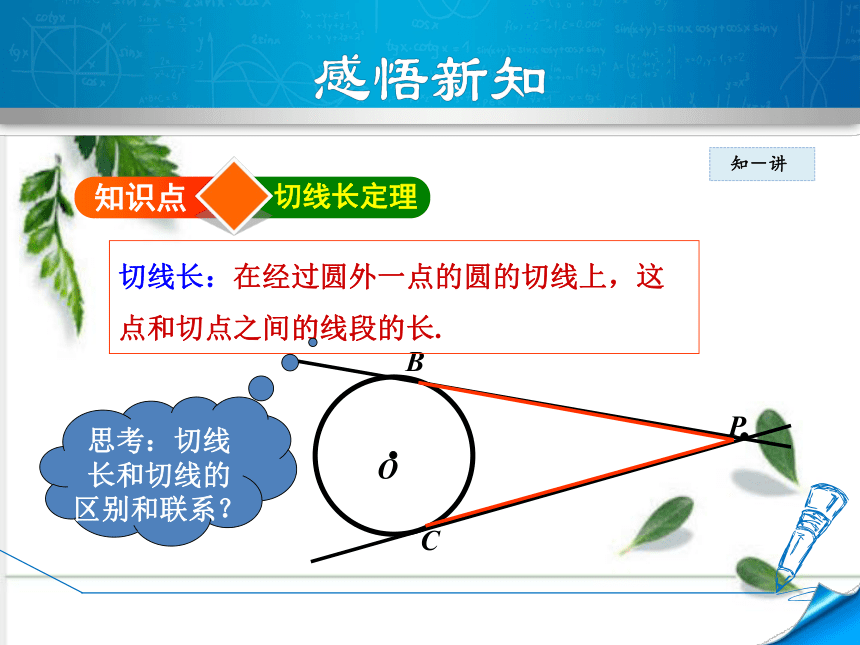
知识点
切线长定理
知-讲
P
B
C
O
切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长.
思考:切线长和切线的区别和联系?
归 纳
知-讲
切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量.
知-讲
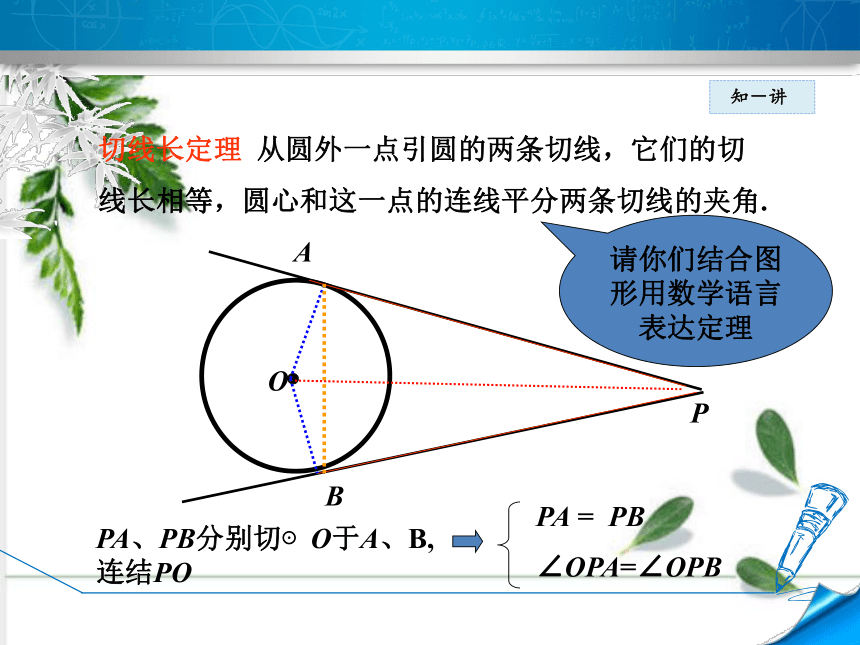
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
P
A
B
O
请你们结合图形用数学语言表达定理
PA、PB分别切⊙O于A、B,连结PO
PA = PB
∠OPA=∠OPB
知-讲
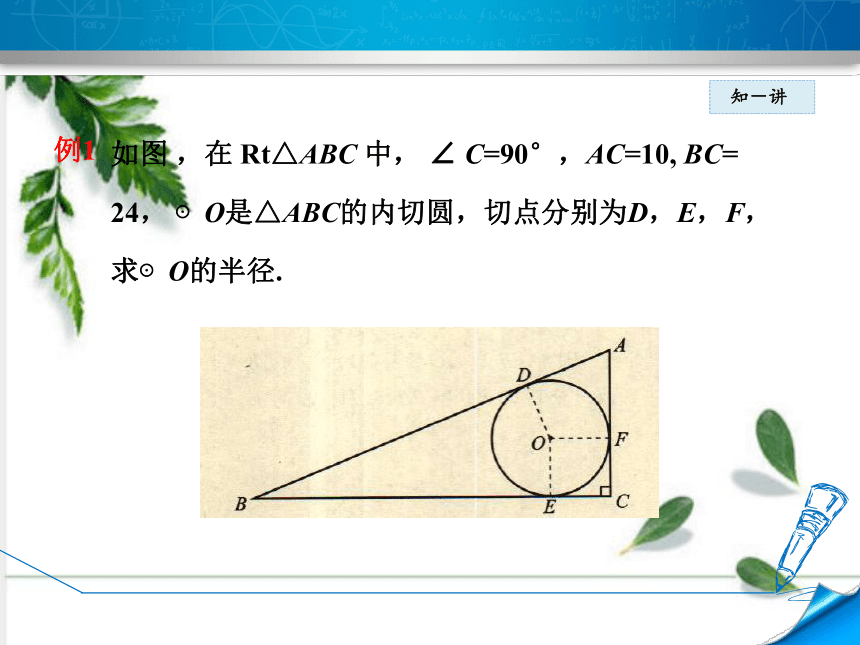
如图 ,在 Rt△ABC 中, ∠ C=90°,AC=10, BC=
24, ⊙O是△ABC的内切圆,切点分别为D,E,F,
求⊙O的半径.
例1
知-讲
解:
连接OD,OE,OF,则OD=OE=OF,设OD=r.
在 △ABC中,AC=10, BC=24,
∴AB = = 26.
∵ ⊙O分别与AB,BC, AC相切于点D,E,F,
∴OD⊥AB,OE ⊥ BC, OF ⊥ AC,BD = BE,
AD = AF,CE=CF.
知-讲
又∵ ∠ C=90°,
∴四边形OECF为正方形.
∴ CE=CF=r.
∴ BE = 24-r, AF=10-r.
∴ AB = BD + AD = BE+AF =24-r+ 10-r= 34-2r.
而AB = 26,
∴ 34 -2r = 26.
∴ r = 4,
即 ⊙O 的半径为4.
已知⊙O的半径为3 cm,点P和圆心O的距离为
6 cm. 过点P画⊙O的两条切线,
求这两条切线的切线长.
知-练
如图,PA,PB为⊙O的切线.
由题意可知OA=3 cm,PO=6 cm,OA⊥PA,∴PA= (cm).
又由切线长定理知PA=PB,
∴PB=33 cm.
解:
2 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
知-练
C
【中考·南充】如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°
知-练
3
C
如图,PA,PB是⊙O的切线,且∠APB=50°,下列结论不正确的是( )
A.PA=PB
B.∠APO=25°
C.∠OBP=65°
D.∠AOP=65°
知1-练
4
C
知-讲
如图,PA,PB是⊙O的切线,切点分别为A,B,BC为⊙O的直径,连接AB,AC,OP.
求证:(1)∠APB=2∠ABC;
(2)AC∥OP.
例2
知-讲
(1)由切线长定理知∠BPO=∠APO= ∠APB,
而要证∠APB=2∠ABC,即证明∠ABC=
∠APB=∠BPO,利用同角的余角相等可证;
(2)证明AC∥OP,可用AC⊥AB,OP⊥AB,也
可用同位角相等来证.
导引:
知-讲
(1)∵PA,PB分别切⊙O于点A,B,
∴由切线长定理知∠BPO=∠APO= ∠APB,
PA=PB,
∴PO⊥AB,∴∠ABP+∠BPO=90°.
又∵PB是⊙O的切线,∴OB⊥PB.
∴∠ABP+∠ABC=90°.
∴∠ABC=∠BPO= ∠APB,
即∠APB=2∠ABC.
证明:
知-讲
(2)∵BC是⊙O的直径,
∴∠BAC=90°,即AC⊥AB.
由(1)知OP⊥AB,∴AC∥OP.
知-讲
总 结
切线长定理的内容揭示两个方面,
一是切线长相等,揭示线段之间的数量关系;
二是与圆心的连线平分两切线的夹角.
这两个方面的内容为证明线段之间的关系或者角之间的关系提供了大量的条件.
为了测量一个圆形铁环的半径,某同学采用如下方法:将铁环平放在水平桌面上,用一个含有30°角的三角尺和一把刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若P为切点,测得PA=5 cm,则铁环的半径是________.
知-练
1
【中考·荆州】如图,过⊙O外一点P引⊙O的两条切线PA,PB,切点分别是A,B,OP交⊙O于点C,点D是优弧AC上不与点A、点C重合的一个动点,连接AD,CD.若∠APB=80°,则∠ADC的度数是( )
A.15°
B.20°
C.25°
D.30°
知-练
2
C
如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别为A,B,点C是劣弧AB上一点,过点C的切线分别交PA,PB于点M,N,若⊙O 的半径为2,∠P=60°,则△PMN的周长为( )
A.4
B.6
C.4
D.6
知-练
3
C
如图,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,AD与CD相交于点D,BC与CD相交于点C,连接OD,OC,对于下列结论:①OD2=DE·CD;②AD+BC=CD;③OD=OC;④S梯形ABCD= CD·OA;⑤∠DOC=90°.其中正确的结论是( )
A.①②⑤
B.②③④
C.③④⑤
D.①④⑤
知-练
4
A
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
1
知识小结
既有外接圆,又有内切圆的平行四边形是( )
A.矩形 B.菱形
C.正方形 D.矩形或菱形
2
易错小结
C
易错点:变式应用切线长定理时因考虑不全而致错.
谢谢!
第7节 切线长定理
1
课堂讲解
切线长定理
2
课时流程
逐点
导讲练
课堂小结
作业提升
前面我们已经学习了切线的判定和性质,已知⊙O和⊙O外一点P,你能够过点P画出⊙O的切线吗?
1.猜想:图中的线段PA与PB有什么关系?
2.图中还有哪些量?猜想它们之间有什么关系?
知识点
切线长定理
知-讲
P
B
C
O
切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长.
思考:切线长和切线的区别和联系?
归 纳
知-讲
切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量.
知-讲
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
P
A
B
O
请你们结合图形用数学语言表达定理
PA、PB分别切⊙O于A、B,连结PO
PA = PB
∠OPA=∠OPB
知-讲
如图 ,在 Rt△ABC 中, ∠ C=90°,AC=10, BC=
24, ⊙O是△ABC的内切圆,切点分别为D,E,F,
求⊙O的半径.
例1
知-讲
解:
连接OD,OE,OF,则OD=OE=OF,设OD=r.
在 △ABC中,AC=10, BC=24,
∴AB = = 26.
∵ ⊙O分别与AB,BC, AC相切于点D,E,F,
∴OD⊥AB,OE ⊥ BC, OF ⊥ AC,BD = BE,
AD = AF,CE=CF.
知-讲
又∵ ∠ C=90°,
∴四边形OECF为正方形.
∴ CE=CF=r.
∴ BE = 24-r, AF=10-r.
∴ AB = BD + AD = BE+AF =24-r+ 10-r= 34-2r.
而AB = 26,
∴ 34 -2r = 26.
∴ r = 4,
即 ⊙O 的半径为4.
已知⊙O的半径为3 cm,点P和圆心O的距离为
6 cm. 过点P画⊙O的两条切线,
求这两条切线的切线长.
知-练
如图,PA,PB为⊙O的切线.
由题意可知OA=3 cm,PO=6 cm,OA⊥PA,∴PA= (cm).
又由切线长定理知PA=PB,
∴PB=33 cm.
解:
2 下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
知-练
C
【中考·南充】如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60°
B.65°
C.70°
D.75°
知-练
3
C
如图,PA,PB是⊙O的切线,且∠APB=50°,下列结论不正确的是( )
A.PA=PB
B.∠APO=25°
C.∠OBP=65°
D.∠AOP=65°
知1-练
4
C
知-讲
如图,PA,PB是⊙O的切线,切点分别为A,B,BC为⊙O的直径,连接AB,AC,OP.
求证:(1)∠APB=2∠ABC;
(2)AC∥OP.
例2
知-讲
(1)由切线长定理知∠BPO=∠APO= ∠APB,
而要证∠APB=2∠ABC,即证明∠ABC=
∠APB=∠BPO,利用同角的余角相等可证;
(2)证明AC∥OP,可用AC⊥AB,OP⊥AB,也
可用同位角相等来证.
导引:
知-讲
(1)∵PA,PB分别切⊙O于点A,B,
∴由切线长定理知∠BPO=∠APO= ∠APB,
PA=PB,
∴PO⊥AB,∴∠ABP+∠BPO=90°.
又∵PB是⊙O的切线,∴OB⊥PB.
∴∠ABP+∠ABC=90°.
∴∠ABC=∠BPO= ∠APB,
即∠APB=2∠ABC.
证明:
知-讲
(2)∵BC是⊙O的直径,
∴∠BAC=90°,即AC⊥AB.
由(1)知OP⊥AB,∴AC∥OP.
知-讲
总 结
切线长定理的内容揭示两个方面,
一是切线长相等,揭示线段之间的数量关系;
二是与圆心的连线平分两切线的夹角.
这两个方面的内容为证明线段之间的关系或者角之间的关系提供了大量的条件.
为了测量一个圆形铁环的半径,某同学采用如下方法:将铁环平放在水平桌面上,用一个含有30°角的三角尺和一把刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若P为切点,测得PA=5 cm,则铁环的半径是________.
知-练
1
【中考·荆州】如图,过⊙O外一点P引⊙O的两条切线PA,PB,切点分别是A,B,OP交⊙O于点C,点D是优弧AC上不与点A、点C重合的一个动点,连接AD,CD.若∠APB=80°,则∠ADC的度数是( )
A.15°
B.20°
C.25°
D.30°
知-练
2
C
如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别为A,B,点C是劣弧AB上一点,过点C的切线分别交PA,PB于点M,N,若⊙O 的半径为2,∠P=60°,则△PMN的周长为( )
A.4
B.6
C.4
D.6
知-练
3
C
如图,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,AD与CD相交于点D,BC与CD相交于点C,连接OD,OC,对于下列结论:①OD2=DE·CD;②AD+BC=CD;③OD=OC;④S梯形ABCD= CD·OA;⑤∠DOC=90°.其中正确的结论是( )
A.①②⑤
B.②③④
C.③④⑤
D.①④⑤
知-练
4
A
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
1
知识小结
既有外接圆,又有内切圆的平行四边形是( )
A.矩形 B.菱形
C.正方形 D.矩形或菱形
2
易错小结
C
易错点:变式应用切线长定理时因考虑不全而致错.
谢谢!
