北师大版数学九年级下册 3.8 圆内接正多边形 课件(31张ppt)
文档属性
| 名称 | 北师大版数学九年级下册 3.8 圆内接正多边形 课件(31张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 23:23:49 | ||
图片预览








文档简介
第三章 圆
第8节 圆内接正多边形
1
课堂讲解
圆内接正多边形
圆内接正多边形的有关概念
正多边形的作图
2
课时流程
逐点
导讲练
课堂小结
作业提升
1.观察下面的三幅图片,说说图片中各包含哪些多边形.
2.日常生活中我们经常看到哪些多边形形状的物体?
1
知识点
圆内接正多边形
顶点都在同一圆上的正多边形叫做圆内接正多边形.
这个圆叫做该正多边 形的外接圆.
知1-导
知1-讲
正n边形的各角相等,且每个内角为:
每个外角为:
知1-讲
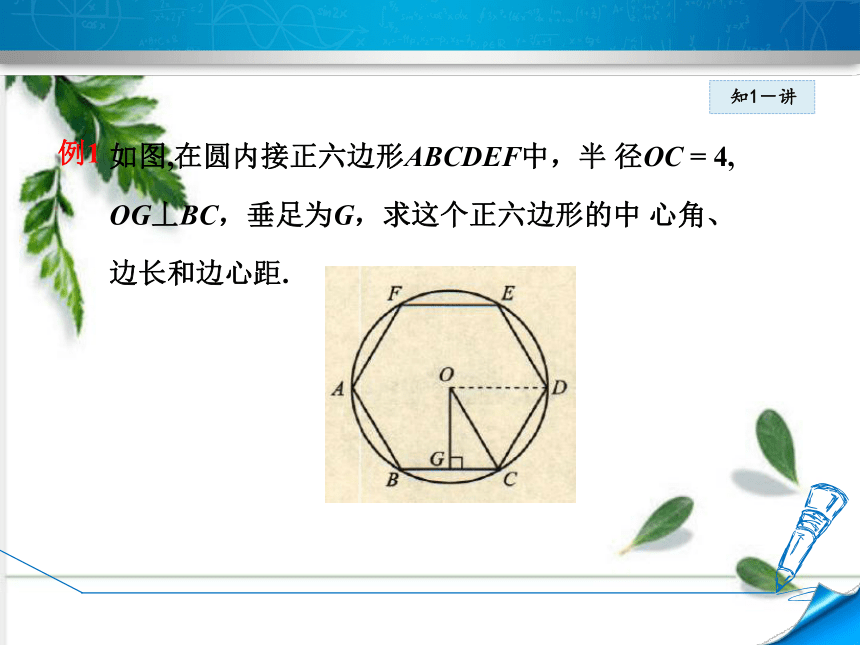
如图,在圆内接正六边形ABCDEF中,半 径OC = 4,
OG丄BC,垂足为G,求这个正六边形的中 心角、
边长和边心距.
例1
知1-讲
解:
连接OD.∵六边形ABCDEF为正六边形,
∴ ∠ COD = = 60°
∴ △COD为等边三角形.
∴ CD = OC = 4.
在 Rt △ COG中,OC = 4,CG= BC= ×4=2,
∴ OG =
∴正六边形的中心角为60°,边长为4,边心距为
知1-讲
如图所示,三角形AOB 是正三角形,以点O 为圆心,
OA 为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O于点D,E,求证:六边形ABCDEF 为圆内接正六边形.
例2
导引:
紧扣正多边形的定义,结合同圆中弧、圆心角的
关系证明.
知1-讲
解:
∵三角形AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°,OB=OA.
∴点B 在⊙ O 上.
∵ FC ∥ AB,∴∠ FOA= ∠ OAB=60°,∠ COB=
∠ OBA=60°.
∴∠ AOB= ∠ BOC= ∠ COD= ∠ DOE= ∠ EOF=
∠ FOA=60° .
∴六边形ABCDEF 为圆内接正六边形.
知1-讲
下列说法不正确的是( )
A.等边三角形是正多边形
B.各边相等,各角也相等的多边形是正多边形
C.菱形不一定是正多边形
D.各角相等的多边形是正多边形
例3
导引:
等边三角形是正三角形;各边相等,各角也相等的多边形是正多边形;当菱形的四个角相等时才是正多边形(正方形),所以菱形不一定是正多边形;D说法不正确. 答案:D
D
总 结
知1-讲
正多边形的识别要从两个角度去看,
一是边都相等;
二是内角都相等.
知1-练
分别求出半径为6 cm的圆内接正三角形的边长和边心距.
1
解:
设正六边形DFHKGE的中心为O,连接OH,OK,则△OHK为等边三角形.
由题意可得OH=HK= BC=2,∠OHK=60°,∴S△OHK= HK·OHsin 60°
= ×2×2× = .
又∵S正六边形=6S△OHK,∴S正六边形=6× =6 .
知1-练
【中考·株洲】下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
正多边形的一边所对的中心角与该多边形的一个内角的关系为( )
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
2
3
A
B
知1-练
一个圆的内接正四边形和外切正四边形的面积的比是( )
A.1∶ B.1∶2
C.2∶3 D.2∶π
4
B
知1-练
【中考·青岛】如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB等
于( )
A.30°
B.45°
C.150°
D.30°或150°
5
A
知1-练
(中考·泸州)以半径为1的圆的内接正三角形、正方
形、正六边形的边心距为三边作三角形,则该三
角形的面积是( )
A. B. C. D.
6
D
知1-练
(中考·泸州)以半径为1的圆的内接正三角形、正方
形、正六边形的边心距为三边作三角形,则该三
角形的面积是( )
A. B. C. D.
6
D
知1-练
(中考·随州)如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2-r2=a2
B.a=2Rsin 36°
C.a=2rtan 36°
D.r=Rcos 36°
7
A
3
知识点
正多边形的作图
知3-导
利用尺规作一个已知圆的内接正六边形.
由于正六边形的中心角为60°,因此它的边长就是其外接圆
的半径R.所 以,在半径为R的圆上,依次截取等于R的弦,
就可以六等分圆,进而作出 圆内接正六边形.
知3-讲
作一个正三角形,使其半径为0.9 cm.
例4
导引:
用量角器画,先求出其中心角;用尺规画,则先考虑等分圆周.
知3-讲
解:
作法一:
(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°;
(3)连接 AB,BC,CA.则△ABC为所求作的正三角
形,如图所示.
知3-讲
作法二:
(1)作半径为0.9 cm的⊙O;
(2)作⊙O的任一直径AB;
(3)分别以A,B为圆心,以0.9 cm为半径作弧,交
⊙O于点C,F和D,E;(4)连接AD,DE,EA.
则△ADE为所求作的正三角形,如图所示.
总 结
知3-讲
1. 画圆的内接正n 边形,实质是找圆的n 等分点.
2. 用量角器等分圆是一种简单常用的方法,但边数很大时,容易产生较大误差.
3. 尺规作图是一种比较准确的等分圆的方法,但只限于作一些特殊的正多边形.
知3-讲
用尺规作圆的内接正方形.
已知:如图,⊙O.
求作:正方形ABCD内接于⊙O.
例5
知3-讲
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
知3-练
如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两
点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
1
C
知3-练
在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).
2
解:
如图所示.
(答案不唯一)
正多边形:各边相等、各角也相等的多边形叫做
正多边形.
把一个圆n(n≥3)等分,顺次连接各等分点,就得
到一个正n边形. 我们把这个正n边形叫做圆的内
接正n边形.
1
知识小结
一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
A.2 B. C.1 D.
2
易错小结
A
易错点:误认为正多边形的边心距是正多边形的半径.
错解:B
诊断:设正多边形的边数为n. 因为正多边形的内角
和为(n-2)·180°,正多边形的外角和为360°,根
据题意得(n-2)·180°=360°×2,解得n=6,故正
多边形为正六边形.边长为2的正六边形可以分成六
个边长为2的正三角形,所以正多边形的半径等于2.
产生错误的原因是认为正多边形的边心距是正多边
形的半径,计算得出错误的结果 ,最后导致错
选B.
谢谢!
第8节 圆内接正多边形
1
课堂讲解
圆内接正多边形
圆内接正多边形的有关概念
正多边形的作图
2
课时流程
逐点
导讲练
课堂小结
作业提升
1.观察下面的三幅图片,说说图片中各包含哪些多边形.
2.日常生活中我们经常看到哪些多边形形状的物体?
1
知识点
圆内接正多边形
顶点都在同一圆上的正多边形叫做圆内接正多边形.
这个圆叫做该正多边 形的外接圆.
知1-导
知1-讲
正n边形的各角相等,且每个内角为:
每个外角为:
知1-讲
如图,在圆内接正六边形ABCDEF中,半 径OC = 4,
OG丄BC,垂足为G,求这个正六边形的中 心角、
边长和边心距.
例1
知1-讲
解:
连接OD.∵六边形ABCDEF为正六边形,
∴ ∠ COD = = 60°
∴ △COD为等边三角形.
∴ CD = OC = 4.
在 Rt △ COG中,OC = 4,CG= BC= ×4=2,
∴ OG =
∴正六边形的中心角为60°,边长为4,边心距为
知1-讲
如图所示,三角形AOB 是正三角形,以点O 为圆心,
OA 为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O于点D,E,求证:六边形ABCDEF 为圆内接正六边形.
例2
导引:
紧扣正多边形的定义,结合同圆中弧、圆心角的
关系证明.
知1-讲
解:
∵三角形AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°,OB=OA.
∴点B 在⊙ O 上.
∵ FC ∥ AB,∴∠ FOA= ∠ OAB=60°,∠ COB=
∠ OBA=60°.
∴∠ AOB= ∠ BOC= ∠ COD= ∠ DOE= ∠ EOF=
∠ FOA=60° .
∴六边形ABCDEF 为圆内接正六边形.
知1-讲
下列说法不正确的是( )
A.等边三角形是正多边形
B.各边相等,各角也相等的多边形是正多边形
C.菱形不一定是正多边形
D.各角相等的多边形是正多边形
例3
导引:
等边三角形是正三角形;各边相等,各角也相等的多边形是正多边形;当菱形的四个角相等时才是正多边形(正方形),所以菱形不一定是正多边形;D说法不正确. 答案:D
D
总 结
知1-讲
正多边形的识别要从两个角度去看,
一是边都相等;
二是内角都相等.
知1-练
分别求出半径为6 cm的圆内接正三角形的边长和边心距.
1
解:
设正六边形DFHKGE的中心为O,连接OH,OK,则△OHK为等边三角形.
由题意可得OH=HK= BC=2,∠OHK=60°,∴S△OHK= HK·OHsin 60°
= ×2×2× = .
又∵S正六边形=6S△OHK,∴S正六边形=6× =6 .
知1-练
【中考·株洲】下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
正多边形的一边所对的中心角与该多边形的一个内角的关系为( )
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
2
3
A
B
知1-练
一个圆的内接正四边形和外切正四边形的面积的比是( )
A.1∶ B.1∶2
C.2∶3 D.2∶π
4
B
知1-练
【中考·青岛】如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB等
于( )
A.30°
B.45°
C.150°
D.30°或150°
5
A
知1-练
(中考·泸州)以半径为1的圆的内接正三角形、正方
形、正六边形的边心距为三边作三角形,则该三
角形的面积是( )
A. B. C. D.
6
D
知1-练
(中考·泸州)以半径为1的圆的内接正三角形、正方
形、正六边形的边心距为三边作三角形,则该三
角形的面积是( )
A. B. C. D.
6
D
知1-练
(中考·随州)如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2-r2=a2
B.a=2Rsin 36°
C.a=2rtan 36°
D.r=Rcos 36°
7
A
3
知识点
正多边形的作图
知3-导
利用尺规作一个已知圆的内接正六边形.
由于正六边形的中心角为60°,因此它的边长就是其外接圆
的半径R.所 以,在半径为R的圆上,依次截取等于R的弦,
就可以六等分圆,进而作出 圆内接正六边形.
知3-讲
作一个正三角形,使其半径为0.9 cm.
例4
导引:
用量角器画,先求出其中心角;用尺规画,则先考虑等分圆周.
知3-讲
解:
作法一:
(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°;
(3)连接 AB,BC,CA.则△ABC为所求作的正三角
形,如图所示.
知3-讲
作法二:
(1)作半径为0.9 cm的⊙O;
(2)作⊙O的任一直径AB;
(3)分别以A,B为圆心,以0.9 cm为半径作弧,交
⊙O于点C,F和D,E;(4)连接AD,DE,EA.
则△ADE为所求作的正三角形,如图所示.
总 结
知3-讲
1. 画圆的内接正n 边形,实质是找圆的n 等分点.
2. 用量角器等分圆是一种简单常用的方法,但边数很大时,容易产生较大误差.
3. 尺规作图是一种比较准确的等分圆的方法,但只限于作一些特殊的正多边形.
知3-讲
用尺规作圆的内接正方形.
已知:如图,⊙O.
求作:正方形ABCD内接于⊙O.
例5
知3-讲
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
知3-练
如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两
点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
1
C
知3-练
在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).
2
解:
如图所示.
(答案不唯一)
正多边形:各边相等、各角也相等的多边形叫做
正多边形.
把一个圆n(n≥3)等分,顺次连接各等分点,就得
到一个正n边形. 我们把这个正n边形叫做圆的内
接正n边形.
1
知识小结
一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
A.2 B. C.1 D.
2
易错小结
A
易错点:误认为正多边形的边心距是正多边形的半径.
错解:B
诊断:设正多边形的边数为n. 因为正多边形的内角
和为(n-2)·180°,正多边形的外角和为360°,根
据题意得(n-2)·180°=360°×2,解得n=6,故正
多边形为正六边形.边长为2的正六边形可以分成六
个边长为2的正三角形,所以正多边形的半径等于2.
产生错误的原因是认为正多边形的边心距是正多边
形的半径,计算得出错误的结果 ,最后导致错
选B.
谢谢!
