华师大版 八年级数学下册 第18章 平行四边形 单元检测卷(Word版 含答案)
文档属性
| 名称 | 华师大版 八年级数学下册 第18章 平行四边形 单元检测卷(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 00:00:00 | ||
图片预览



文档简介
第18章 单元检测卷
(考试时间:45分钟 总分:100分)
姓名:________________ 班级:________________
一、选择题(每小题4分,共32分)
1.在?ABCD中,若∠A=50°,则下列各式中,不能成立的是( )
A.∠B=130°
B.∠B+∠C=180°
C.∠C=50°
D.∠B+∠D=180°
2.四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.OA=OC,OB=OD
B.AD∥BC,AB∥DC
C.AB=DC,AD=BC
D.AB∥DC,AD=BC
3.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD的周长是( )
A.22
B.20
C.22或20
D.18
4.如图,在?ABCD中,已知AB=5,AD=2,DE平分∠ADC交AB于E,则BE的值为( )
A.3
B.2.5
C.3.5
D.2
5.如图所示,在平面直角坐标系中,原点O恰好是?ABCD对角线的交点.若A点的坐标为(2,3),则C点的坐标为( )
A.(-3,-2)
B.(-2,3)
C.(-2,-3)
D.(2,-3)
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE=( )
A.2
B.4
C.4
D.8
7.如图所示,P是平行四边形ABCD内部任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
A.S1+S2>S3+S4
B.S1+S2=S3+S4
C.S1+S2D.S1+S3=S2+S4
8.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;
④PF=PC.
其中正确结论的个数为( )
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共24分)
9.在四边形ABCD中,AB=CD,AD=BC,若∠A+∠C=160°,则∠D=____°.
10.已知平行四边形的面积是144
cm2,相邻两边上的高分别为8
cm和9
cm,则这个平行四边形的周长为____.
11.如图所示,?ABCD的对角线AC,BD相交于点O,若△AOB的面积为6
cm2,则?ABCD的面积为____.
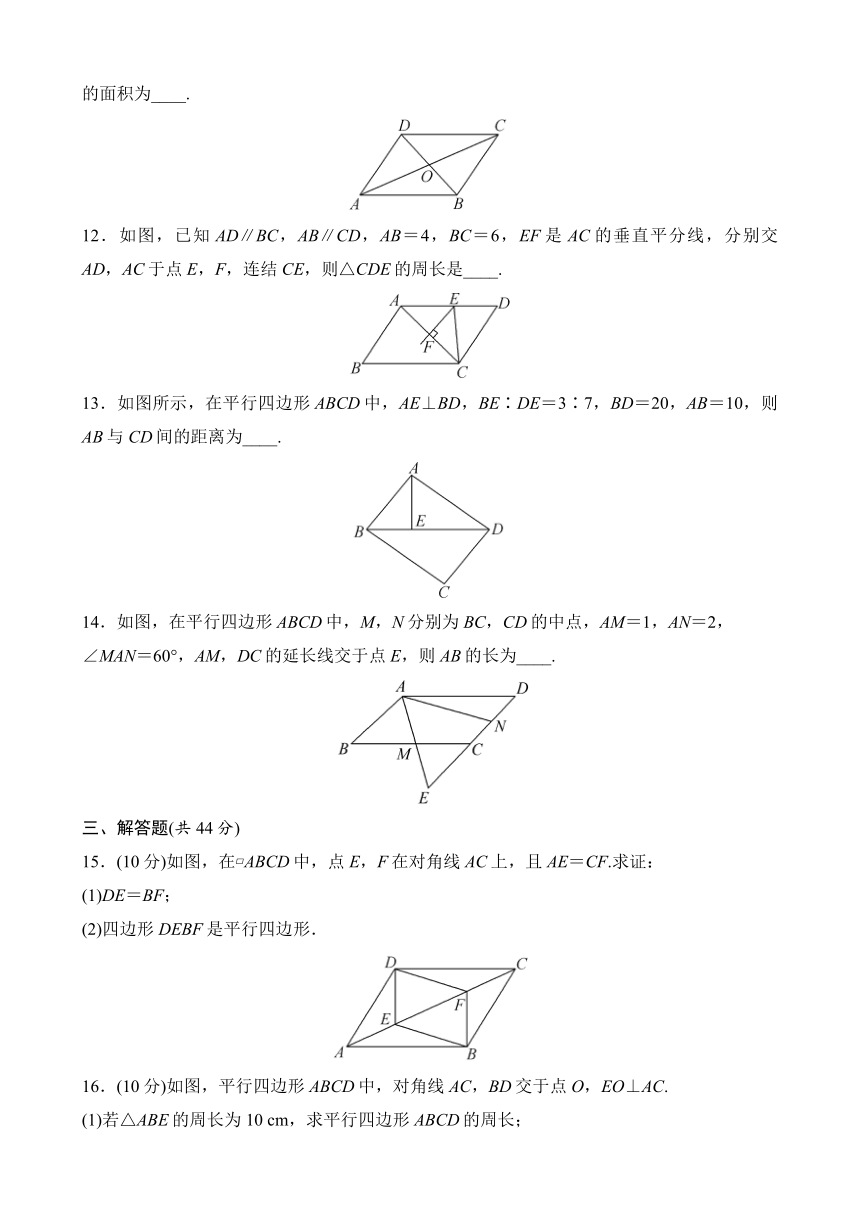
12.如图,已知AD∥BC,AB∥CD,AB=4,BC=6,EF是AC的垂直平分线,分别交AD,AC于点E,F,连结CE,则△CDE的周长是____.
13.如图所示,在平行四边形ABCD中,AE⊥BD,BE∶DE=3∶7,BD=20,AB=10,则AB与CD间的距离为____.
14.如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM,DC的延长线交于点E,则AB的长为____.
三、解答题(共44分)
15.(10分)如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
16.(10分)如图,平行四边形ABCD中,对角线AC,BD交于点O,EO⊥AC.
(1)若△ABE的周长为10
cm,求平行四边形ABCD的周长;
(2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数.
17.(12分)如图所示,在平行四边形ABCD中,AE,BF分别平分∠DAB和∠ABC,交CD于点E,F,AE,BF相交于点M.
(1)试证明:△BCF为等腰三角形;
(2)若AB=5,DF=1,求EF的长.
18.(12分)已知:如图所示,在?ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG=DH.
(1)若AC=6,BD=8,试求AD的取值范围;
(2)若AC=AD,∠CAD=50°,试求∠ABC的度数;
(3)求证:四边形EHFG是平行四边形.
第18章 单元检测卷
(考试时间:45分钟 总分:100分)
姓名:________________ 班级:________________
一、选择题(每小题4分,共32分)
1.在?ABCD中,若∠A=50°,则下列各式中,不能成立的是( D )
A.∠B=130°
B.∠B+∠C=180°
C.∠C=50°
D.∠B+∠D=180°
2.四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( D )
A.OA=OC,OB=OD
B.AD∥BC,AB∥DC
C.AB=DC,AD=BC
D.AB∥DC,AD=BC
3.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD的周长是( C )
A.22
B.20
C.22或20
D.18
4.如图,在?ABCD中,已知AB=5,AD=2,DE平分∠ADC交AB于E,则BE的值为( A )
A.3
B.2.5
C.3.5
D.2
5.如图所示,在平面直角坐标系中,原点O恰好是?ABCD对角线的交点.若A点的坐标为(2,3),则C点的坐标为( C )
A.(-3,-2)
B.(-2,3)
C.(-2,-3)
D.(2,-3)
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE=( B )
A.2
B.4
C.4
D.8
7.如图所示,P是平行四边形ABCD内部任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( D )
A.S1+S2>S3+S4
B.S1+S2=S3+S4
C.S1+S2D.S1+S3=S2+S4
8.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;
④PF=PC.
其中正确结论的个数为( D )
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共24分)
9.在四边形ABCD中,AB=CD,AD=BC,若∠A+∠C=160°,则∠D=__100__°.
10.已知平行四边形的面积是144
cm2,相邻两边上的高分别为8
cm和9
cm,则这个平行四边形的周长为__68__cm__.
11.如图所示,?ABCD的对角线AC,BD相交于点O,若△AOB的面积为6
cm2,则?ABCD的面积为__24__cm2__.
12.如图,已知AD∥BC,AB∥CD,AB=4,BC=6,EF是AC的垂直平分线,分别交AD,AC于点E,F,连结CE,则△CDE的周长是__10__.
13.如图所示,在平行四边形ABCD中,AE⊥BD,BE∶DE=3∶7,BD=20,AB=10,则AB与CD间的距离为__16__.
14.如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM,DC的延长线交于点E,则AB的长为____.
三、解答题(共44分)
15.(10分)如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,∴∠DAE=∠BCF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),∴DE=BF.
(2)由(1)可得△ADE≌△CBF,∴∠ADE=∠CBF.
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE,∴DE∥BF.又∵DE=BF,
∴四边形DEBF是平行四边形.
16.(10分)如图,平行四边形ABCD中,对角线AC,BD交于点O,EO⊥AC.
(1)若△ABE的周长为10
cm,求平行四边形ABCD的周长;
(2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数.
解:(1)∵四边形ABCD是平行四边形,∴OA=OC.
∵OE⊥AC,∴AE=CE,
∴△ABE的周长为AB+BE+AE=AB+BC=10
cm,
∴平行四边形ABCD的周长为2×10=20(cm).
(2)由(1)知AE=CE,∴∠EAC=∠ECA.
∵AE平分∠BAC,∴∠BAE=∠EAC=∠ECA.
又∵在△ABC中,∠ABC=78°,
∴3∠ECA+78°=180°,∴∠ECA=34°.
∵AD∥BC,∴∠DAC=∠ECA=34°.
17.(12分)如图所示,在平行四边形ABCD中,AE,BF分别平分∠DAB和∠ABC,交CD于点E,F,AE,BF相交于点M.
(1)试证明:△BCF为等腰三角形;
(2)若AB=5,DF=1,求EF的长.
解:(1)证明:在?ABCD中,AB∥CD,
∴∠ABF=∠CFB.
∵BF平分∠ABC,∴∠ABF=∠CBF,
∴∠CBF=∠CFB,∴CF=CB,
∴△BCF是等腰三角形.
(2)∵在平行四边形ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又AE平分∠DAB,∴∠DAE=∠EAB,
∴∠DEA=∠DAE,∴DE=AD.
同理可得CF=BC.
又∵AD=BC,∴DE=CF,
∴DE-EF=CF-EF,即DF=CE=1,
∴EF=3.
18.(12分)已知:如图所示,在?ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG=DH.
(1)若AC=6,BD=8,试求AD的取值范围;
(2)若AC=AD,∠CAD=50°,试求∠ABC的度数;
(3)求证:四边形EHFG是平行四边形.
解:(1)在?ABCD中,OA=OC,OB=OD,
∴OA=AC=3,OD=BD=4.
在△AOD中,4-3(2)∵AC=AD,∴∠ACD=∠ADC.
又∵∠CAD=50°,∴∠ADC==65°.
在?ABCD中,∠ABC=∠ADC=65°.
(3)证明:在?ABCD中,OA=OC,OB=OD,
∵AE=CF,∴OA-AE=OC-CF,即OE=OF.
∵BG=DH,∴OB-BG=OD-DH,即OG=OH.
∴四边形EHFG是平行四边形.
(考试时间:45分钟 总分:100分)
姓名:________________ 班级:________________
一、选择题(每小题4分,共32分)
1.在?ABCD中,若∠A=50°,则下列各式中,不能成立的是( )
A.∠B=130°
B.∠B+∠C=180°
C.∠C=50°
D.∠B+∠D=180°
2.四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.OA=OC,OB=OD
B.AD∥BC,AB∥DC
C.AB=DC,AD=BC
D.AB∥DC,AD=BC
3.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD的周长是( )
A.22
B.20
C.22或20
D.18
4.如图,在?ABCD中,已知AB=5,AD=2,DE平分∠ADC交AB于E,则BE的值为( )
A.3
B.2.5
C.3.5
D.2
5.如图所示,在平面直角坐标系中,原点O恰好是?ABCD对角线的交点.若A点的坐标为(2,3),则C点的坐标为( )
A.(-3,-2)
B.(-2,3)
C.(-2,-3)
D.(2,-3)
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE=( )
A.2
B.4
C.4
D.8
7.如图所示,P是平行四边形ABCD内部任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
A.S1+S2>S3+S4
B.S1+S2=S3+S4
C.S1+S2
8.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;
④PF=PC.
其中正确结论的个数为( )
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共24分)
9.在四边形ABCD中,AB=CD,AD=BC,若∠A+∠C=160°,则∠D=____°.
10.已知平行四边形的面积是144
cm2,相邻两边上的高分别为8
cm和9
cm,则这个平行四边形的周长为____.
11.如图所示,?ABCD的对角线AC,BD相交于点O,若△AOB的面积为6
cm2,则?ABCD的面积为____.
12.如图,已知AD∥BC,AB∥CD,AB=4,BC=6,EF是AC的垂直平分线,分别交AD,AC于点E,F,连结CE,则△CDE的周长是____.
13.如图所示,在平行四边形ABCD中,AE⊥BD,BE∶DE=3∶7,BD=20,AB=10,则AB与CD间的距离为____.
14.如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM,DC的延长线交于点E,则AB的长为____.
三、解答题(共44分)
15.(10分)如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
16.(10分)如图,平行四边形ABCD中,对角线AC,BD交于点O,EO⊥AC.
(1)若△ABE的周长为10
cm,求平行四边形ABCD的周长;
(2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数.
17.(12分)如图所示,在平行四边形ABCD中,AE,BF分别平分∠DAB和∠ABC,交CD于点E,F,AE,BF相交于点M.
(1)试证明:△BCF为等腰三角形;
(2)若AB=5,DF=1,求EF的长.
18.(12分)已知:如图所示,在?ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG=DH.
(1)若AC=6,BD=8,试求AD的取值范围;
(2)若AC=AD,∠CAD=50°,试求∠ABC的度数;
(3)求证:四边形EHFG是平行四边形.
第18章 单元检测卷
(考试时间:45分钟 总分:100分)
姓名:________________ 班级:________________
一、选择题(每小题4分,共32分)
1.在?ABCD中,若∠A=50°,则下列各式中,不能成立的是( D )
A.∠B=130°
B.∠B+∠C=180°
C.∠C=50°
D.∠B+∠D=180°
2.四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( D )
A.OA=OC,OB=OD
B.AD∥BC,AB∥DC
C.AB=DC,AD=BC
D.AB∥DC,AD=BC
3.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD的周长是( C )
A.22
B.20
C.22或20
D.18
4.如图,在?ABCD中,已知AB=5,AD=2,DE平分∠ADC交AB于E,则BE的值为( A )
A.3
B.2.5
C.3.5
D.2
5.如图所示,在平面直角坐标系中,原点O恰好是?ABCD对角线的交点.若A点的坐标为(2,3),则C点的坐标为( C )
A.(-3,-2)
B.(-2,3)
C.(-2,-3)
D.(2,-3)
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE=( B )
A.2
B.4
C.4
D.8
7.如图所示,P是平行四边形ABCD内部任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( D )
A.S1+S2>S3+S4
B.S1+S2=S3+S4
C.S1+S2
8.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;
④PF=PC.
其中正确结论的个数为( D )
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共24分)
9.在四边形ABCD中,AB=CD,AD=BC,若∠A+∠C=160°,则∠D=__100__°.
10.已知平行四边形的面积是144
cm2,相邻两边上的高分别为8
cm和9
cm,则这个平行四边形的周长为__68__cm__.
11.如图所示,?ABCD的对角线AC,BD相交于点O,若△AOB的面积为6
cm2,则?ABCD的面积为__24__cm2__.
12.如图,已知AD∥BC,AB∥CD,AB=4,BC=6,EF是AC的垂直平分线,分别交AD,AC于点E,F,连结CE,则△CDE的周长是__10__.
13.如图所示,在平行四边形ABCD中,AE⊥BD,BE∶DE=3∶7,BD=20,AB=10,则AB与CD间的距离为__16__.
14.如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM,DC的延长线交于点E,则AB的长为____.
三、解答题(共44分)
15.(10分)如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,∴∠DAE=∠BCF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),∴DE=BF.
(2)由(1)可得△ADE≌△CBF,∴∠ADE=∠CBF.
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE,∴DE∥BF.又∵DE=BF,
∴四边形DEBF是平行四边形.
16.(10分)如图,平行四边形ABCD中,对角线AC,BD交于点O,EO⊥AC.
(1)若△ABE的周长为10
cm,求平行四边形ABCD的周长;
(2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数.
解:(1)∵四边形ABCD是平行四边形,∴OA=OC.
∵OE⊥AC,∴AE=CE,
∴△ABE的周长为AB+BE+AE=AB+BC=10
cm,
∴平行四边形ABCD的周长为2×10=20(cm).
(2)由(1)知AE=CE,∴∠EAC=∠ECA.
∵AE平分∠BAC,∴∠BAE=∠EAC=∠ECA.
又∵在△ABC中,∠ABC=78°,
∴3∠ECA+78°=180°,∴∠ECA=34°.
∵AD∥BC,∴∠DAC=∠ECA=34°.
17.(12分)如图所示,在平行四边形ABCD中,AE,BF分别平分∠DAB和∠ABC,交CD于点E,F,AE,BF相交于点M.
(1)试证明:△BCF为等腰三角形;
(2)若AB=5,DF=1,求EF的长.
解:(1)证明:在?ABCD中,AB∥CD,
∴∠ABF=∠CFB.
∵BF平分∠ABC,∴∠ABF=∠CBF,
∴∠CBF=∠CFB,∴CF=CB,
∴△BCF是等腰三角形.
(2)∵在平行四边形ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又AE平分∠DAB,∴∠DAE=∠EAB,
∴∠DEA=∠DAE,∴DE=AD.
同理可得CF=BC.
又∵AD=BC,∴DE=CF,
∴DE-EF=CF-EF,即DF=CE=1,
∴EF=3.
18.(12分)已知:如图所示,在?ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG=DH.
(1)若AC=6,BD=8,试求AD的取值范围;
(2)若AC=AD,∠CAD=50°,试求∠ABC的度数;
(3)求证:四边形EHFG是平行四边形.
解:(1)在?ABCD中,OA=OC,OB=OD,
∴OA=AC=3,OD=BD=4.
在△AOD中,4-3
又∵∠CAD=50°,∴∠ADC==65°.
在?ABCD中,∠ABC=∠ADC=65°.
(3)证明:在?ABCD中,OA=OC,OB=OD,
∵AE=CF,∴OA-AE=OC-CF,即OE=OF.
∵BG=DH,∴OB-BG=OD-DH,即OG=OH.
∴四边形EHFG是平行四边形.
