人教版七年级上册数学随堂精炼4.4 课题学习 设计制作长方体形状的包装纸盒(word版,含答案)
文档属性
| 名称 | 人教版七年级上册数学随堂精炼4.4 课题学习 设计制作长方体形状的包装纸盒(word版,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 00:00:00 | ||
图片预览


文档简介
4.4 课题学习 设计制作长方体形状的包装纸盒
一、选择题(共15小题;共75分)
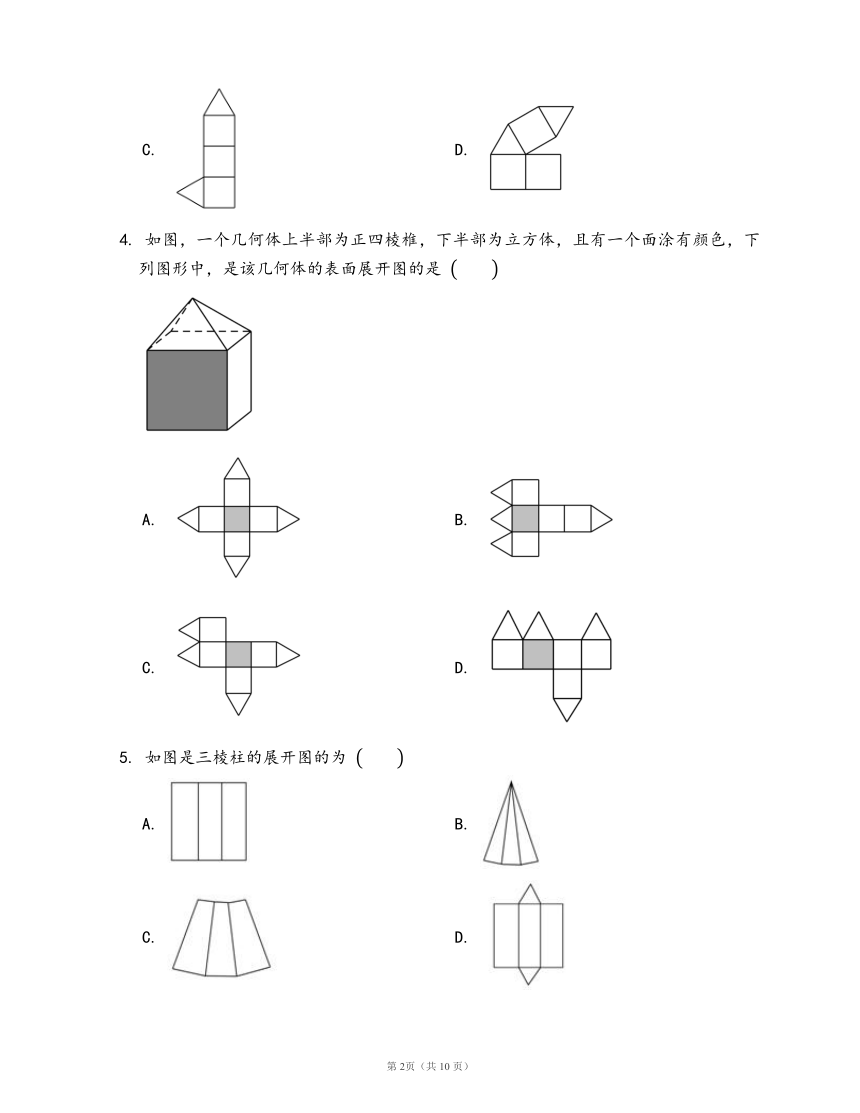
1. 如图,一个几何体上半部为正四棱锥,下半部为正方体,且只有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是 ??
A. B.
C. D.
2. 下列平面图形经过折叠不能围成棱柱的是 ??
A. B.
C. D.
3. 把下图中的三棱柱展开,所得到的展开图是 ??
A. B.
C. D.
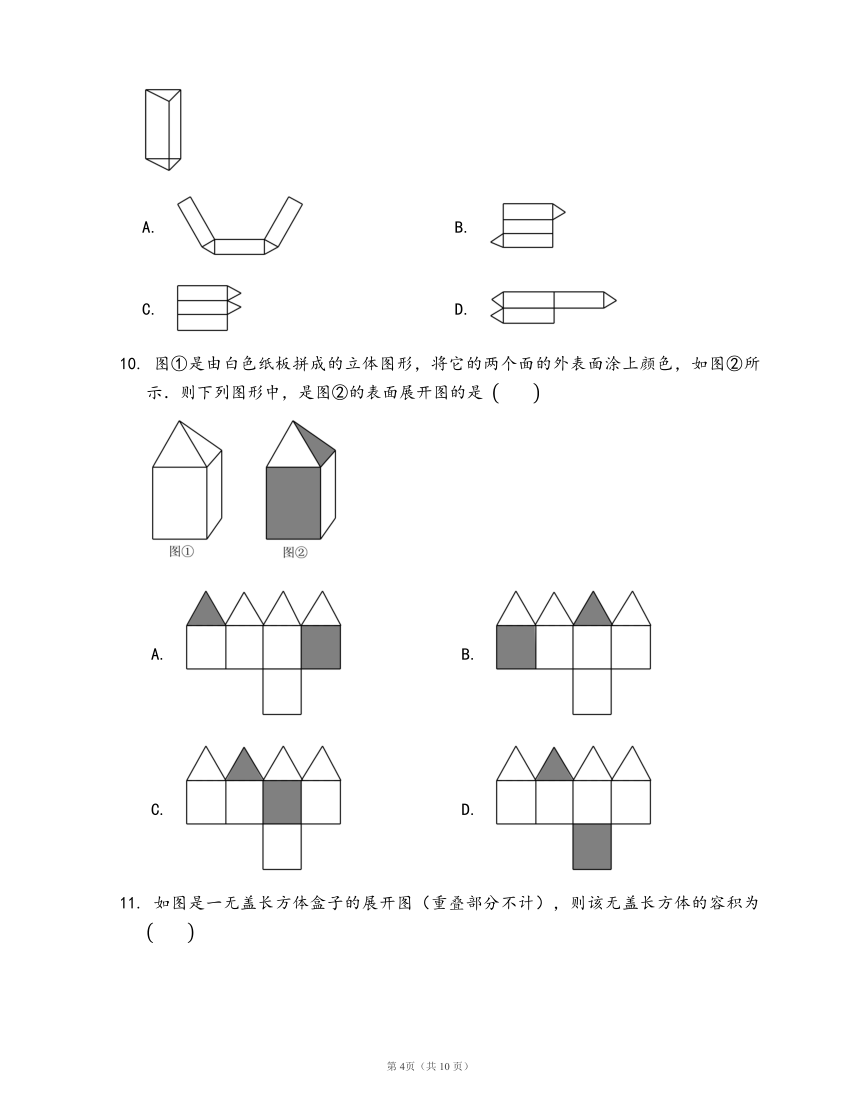
4. 如图,一个几何体上半部为正四棱椎,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是 ??
A. B.
C. D.
5. 如图是三棱柱的展开图的为 ??
A. B.
C. D.
6. 已知 BC 是圆柱底面的直径,AB 是圆柱的高,在圆柱的侧面上,过点 A,C 嵌有一圈路径最短的金属丝,现将圆柱侧面沿 AB 剪开,所得的圆柱的侧面展开图是 ??
A. B.
C. D.
7. 已知 AB 是圆锥(如图1)底面的直径,P 是圆锥的顶点,此圆锥的侧面展开图如图2所示. 一只蚂蚁从 A 点出发,沿着圆锥侧面经过 PB 上一点,最后回到 A 点. 若此蚂蚁所走的路线最短,那么 M , N , S , T ( M , N , S , T 均在 PB 上)四个点中,它最有可能经过的点是 ??
A. M B. N C. S D. T
8. 下面四个图形中,是三棱锥的平面展开图的是 ??
A. B.
C. D.
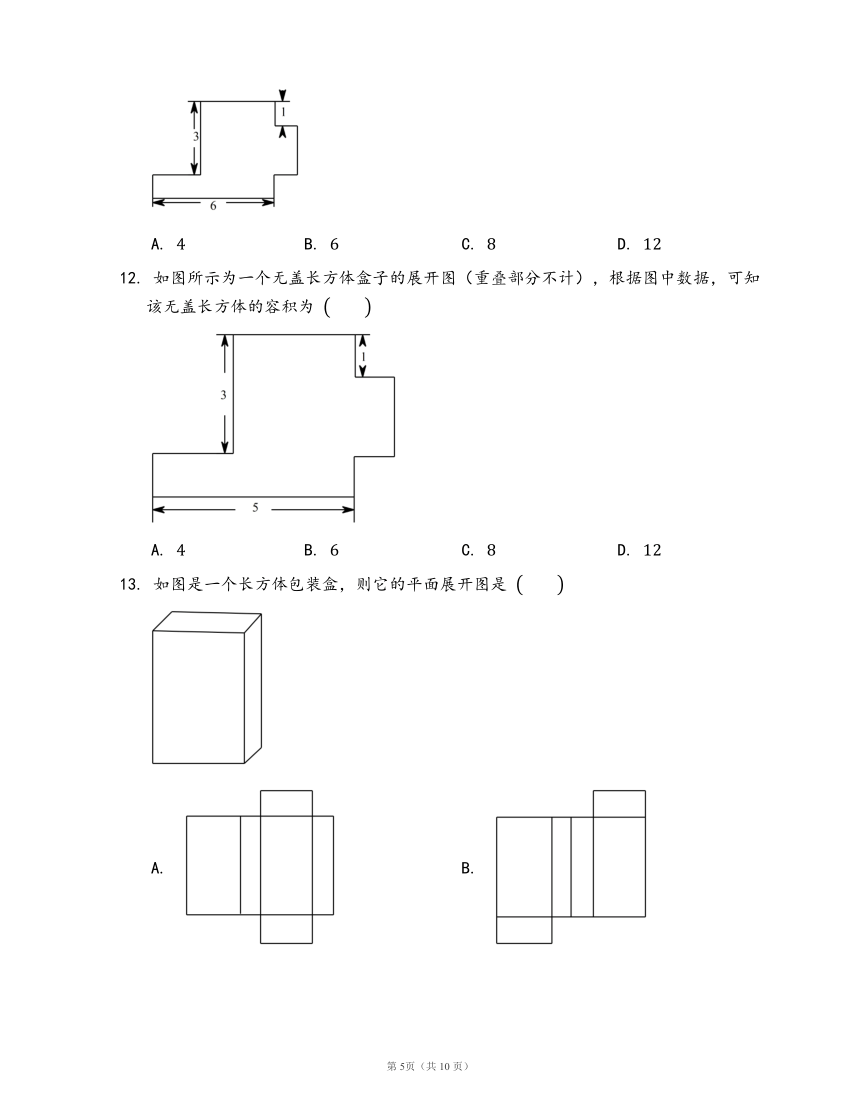
9. 如图是一个三棱柱,下列图形中,能通过折叠围成一个三棱柱的是 ??
A. B.
C. D.
10. 图①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②所示.则下列图形中,是图②的表面展开图的是 ??
A. B.
C. D.
11. 如图是一无盖长方体盒子的展开图(重叠部分不计),则该无盖长方体的容积为 ??
A. 4 B. 6 C. 8 D. 12
12. 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为 ??
A. 4 B. 6 C. 8 D. 12
13. 如图是一个长方体包装盒,则它的平面展开图是 ??
A. B.
C. D.
14. 把如图中的三棱柱展开,所得到的展开图是 ??
A. B.
C. D.
15. 如图是一个长方体纸盒,它的展开图可能是 ??
A. B.
C. D.
二、填空题(共5小题;共30分)
16. 如图是某几何体的展开图,那么这个几何体是 ? .
17. 通过设计和制作长方体的包装纸盒的实践活动,可以进一步体会 ? 图形和 ? 图形之间的相互转化.
18. 把下图折叠一下,它能折成 ?.
19. 设计长方体的包装盒,要先绘制长方体的 ?,再把它剪出并折叠成长方体.此外,还会用到 ? 知识、 ? 知识、 ? 等.
20. 长方体的表面沿某些棱剪开,展开成平面图形,共有 ? 个 ? 形,其中剪的过程中,需要剪 ? 条棱.
三、解答题(共3小题;共45分)
21. 如图是一个食品包装盒的表面展开图.
(1)请写出该包装盒的几何体名称;
(2)根据图中所标尺寸,用 a , b 表示这个几何体的全面积( 侧面积与底面积之和 ),并计算当 a=1 , b=4 时,S 的值.
22. 一个多面体每个面上都标注了字母,如图所示是这个多面体的展开图,请你根据要求回答问题.
(1)如果 A 面在多面体的底部,那么哪一个面在上面?
(2)如果 F 面在前面,B 面在左面,那么哪一个面在上面?
(3)如果 C 面在右面,D 面在后面,那么哪一个面在上面?
23. 下面的两个图形通过折叠,能围成什么几何体?
答案
第一部分
1. D
2. D
3. B
4. B
5. D
6. C
7. B
8. B
9. B
10. A
11. C
12. B
13. A
14. B 【解析】根据两个全等的三角形,在侧面三个长方形的两侧,这样的图形围成的是三棱柱.
把图中的三棱柱展开,所得到的展开图是 B.
15. A
第二部分
16. 圆柱
17. 立体,平面
18. 长方体
19. 展开图,美术,语言,生产常识
20. 6,长方,7
第三部分
21. (1) 长方体;
??????(2) S=2ab×2+2×2a×a+2×a×b=4ab+4a2+2ab=6ab+4a2.
当 a=1 , b=4 时,S=6×1×4+4×12=28.
22. (1) F
??????(2) C
??????(3) A
23. 长方体盒子.
一、选择题(共15小题;共75分)
1. 如图,一个几何体上半部为正四棱锥,下半部为正方体,且只有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是 ??
A. B.
C. D.
2. 下列平面图形经过折叠不能围成棱柱的是 ??
A. B.
C. D.
3. 把下图中的三棱柱展开,所得到的展开图是 ??
A. B.
C. D.
4. 如图,一个几何体上半部为正四棱椎,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是 ??
A. B.
C. D.
5. 如图是三棱柱的展开图的为 ??
A. B.
C. D.
6. 已知 BC 是圆柱底面的直径,AB 是圆柱的高,在圆柱的侧面上,过点 A,C 嵌有一圈路径最短的金属丝,现将圆柱侧面沿 AB 剪开,所得的圆柱的侧面展开图是 ??
A. B.
C. D.
7. 已知 AB 是圆锥(如图1)底面的直径,P 是圆锥的顶点,此圆锥的侧面展开图如图2所示. 一只蚂蚁从 A 点出发,沿着圆锥侧面经过 PB 上一点,最后回到 A 点. 若此蚂蚁所走的路线最短,那么 M , N , S , T ( M , N , S , T 均在 PB 上)四个点中,它最有可能经过的点是 ??
A. M B. N C. S D. T
8. 下面四个图形中,是三棱锥的平面展开图的是 ??
A. B.
C. D.
9. 如图是一个三棱柱,下列图形中,能通过折叠围成一个三棱柱的是 ??
A. B.
C. D.
10. 图①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②所示.则下列图形中,是图②的表面展开图的是 ??
A. B.
C. D.
11. 如图是一无盖长方体盒子的展开图(重叠部分不计),则该无盖长方体的容积为 ??
A. 4 B. 6 C. 8 D. 12
12. 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为 ??
A. 4 B. 6 C. 8 D. 12
13. 如图是一个长方体包装盒,则它的平面展开图是 ??
A. B.
C. D.
14. 把如图中的三棱柱展开,所得到的展开图是 ??
A. B.
C. D.
15. 如图是一个长方体纸盒,它的展开图可能是 ??
A. B.
C. D.
二、填空题(共5小题;共30分)
16. 如图是某几何体的展开图,那么这个几何体是 ? .
17. 通过设计和制作长方体的包装纸盒的实践活动,可以进一步体会 ? 图形和 ? 图形之间的相互转化.
18. 把下图折叠一下,它能折成 ?.
19. 设计长方体的包装盒,要先绘制长方体的 ?,再把它剪出并折叠成长方体.此外,还会用到 ? 知识、 ? 知识、 ? 等.
20. 长方体的表面沿某些棱剪开,展开成平面图形,共有 ? 个 ? 形,其中剪的过程中,需要剪 ? 条棱.
三、解答题(共3小题;共45分)
21. 如图是一个食品包装盒的表面展开图.
(1)请写出该包装盒的几何体名称;
(2)根据图中所标尺寸,用 a , b 表示这个几何体的全面积( 侧面积与底面积之和 ),并计算当 a=1 , b=4 时,S 的值.
22. 一个多面体每个面上都标注了字母,如图所示是这个多面体的展开图,请你根据要求回答问题.
(1)如果 A 面在多面体的底部,那么哪一个面在上面?
(2)如果 F 面在前面,B 面在左面,那么哪一个面在上面?
(3)如果 C 面在右面,D 面在后面,那么哪一个面在上面?
23. 下面的两个图形通过折叠,能围成什么几何体?
答案
第一部分
1. D
2. D
3. B
4. B
5. D
6. C
7. B
8. B
9. B
10. A
11. C
12. B
13. A
14. B 【解析】根据两个全等的三角形,在侧面三个长方形的两侧,这样的图形围成的是三棱柱.
把图中的三棱柱展开,所得到的展开图是 B.
15. A
第二部分
16. 圆柱
17. 立体,平面
18. 长方体
19. 展开图,美术,语言,生产常识
20. 6,长方,7
第三部分
21. (1) 长方体;
??????(2) S=2ab×2+2×2a×a+2×a×b=4ab+4a2+2ab=6ab+4a2.
当 a=1 , b=4 时,S=6×1×4+4×12=28.
22. (1) F
??????(2) C
??????(3) A
23. 长方体盒子.
