人教版七年级上册数学一课一练 4.1 几何图形(word版,含答案)
文档属性
| 名称 | 人教版七年级上册数学一课一练 4.1 几何图形(word版,含答案) | 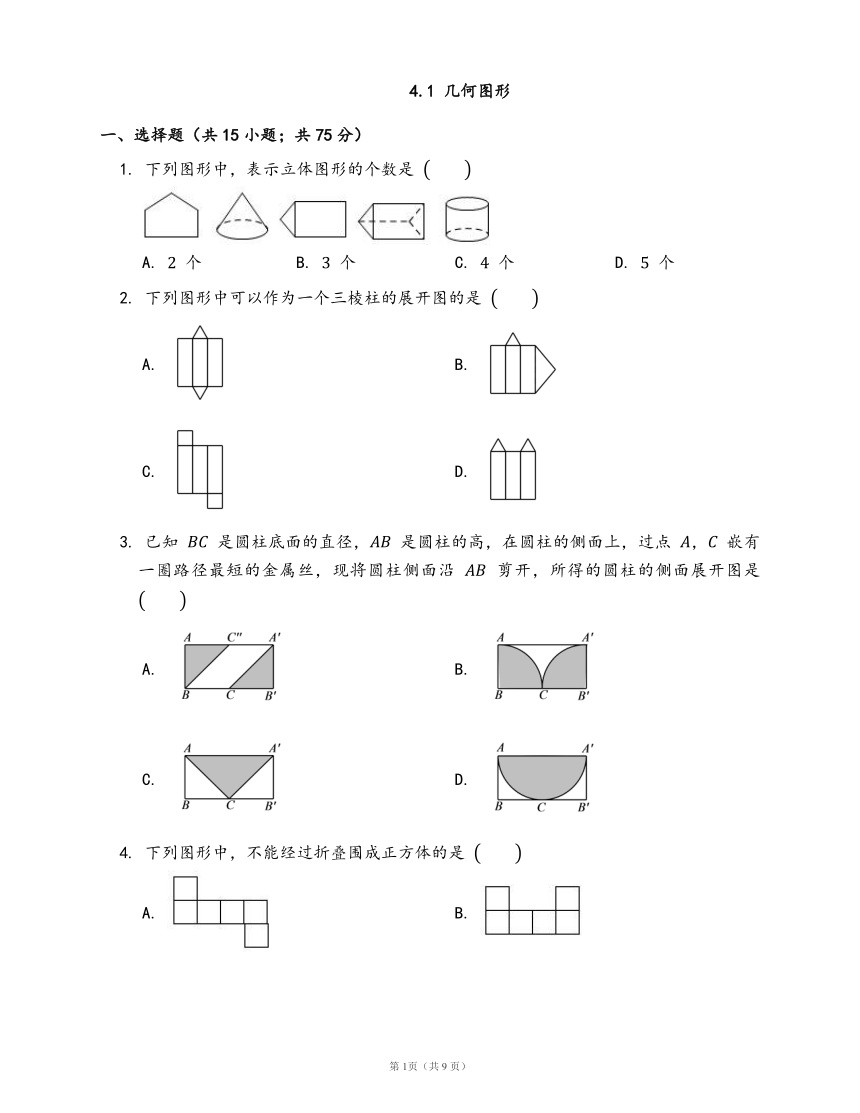 | |
| 格式 | docx | ||
| 文件大小 | 777.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 21:30:40 | ||
图片预览



文档简介
4.1 几何图形
一、选择题(共15小题;共75分)
1. 下列图形中,表示立体图形的个数是 ??
A. 2 个 B. 3 个 C. 4 个 D. 5 个
2. 下列图形中可以作为一个三棱柱的展开图的是 ??
A. B.
C. D.
3. 已知 BC 是圆柱底面的直径,AB 是圆柱的高,在圆柱的侧面上,过点 A,C 嵌有一圈路径最短的金属丝,现将圆柱侧面沿 AB 剪开,所得的圆柱的侧面展开图是 ??
A. B.
C. D.
4. 下列图形中,不能经过折叠围成正方体的是 ??
A. B.
C. D.
5. 把右图中的三棱柱展开,所得到的展开图是 ??
A. B.
C. D.
6. 某几何体由一些大小相同的小正方体组成,如图分别是它的主视图和俯视图,那么要组成该几何体,至少需要多少个这样的小正方体 ??
A. 3 B. 4 C. 5 D. 6
7. 小亮将考试时自勉的话"沉稳、细心、规范"写在一个正方体的六个面上,其平面展开图如图所示,那么该正方体中和"稳"字相对的字是 ??
A. 细 B. 心 C. 规 D. 范
8. 小明用如图所示的胶滚从左到右的方向将图案涂到墙上,符合图示胶滚涂出的图案是 ??
A. B.
C. D.
9. 如图,是一个几何体的三视图,则该几何体的展开图为 ??
A. B.
C. D.
10. 如图,是正方体的平面展开图,每个面上都标有一个汉字,与“爱”字对应的面上的字为 ??
A. 顺 B. 义 C. 家 D. 乡
11. 如图,S 是圆锥的顶点,AB 是圆锥底面的直径,M 是 SA 的中点.在圆锥的侧面上过点 B,M 嵌有一圈路径最短的金属丝,现将圆锥侧面沿 SA 剪开,所得圆锥的侧面展开图可能是 ??
A. B.
C. D.
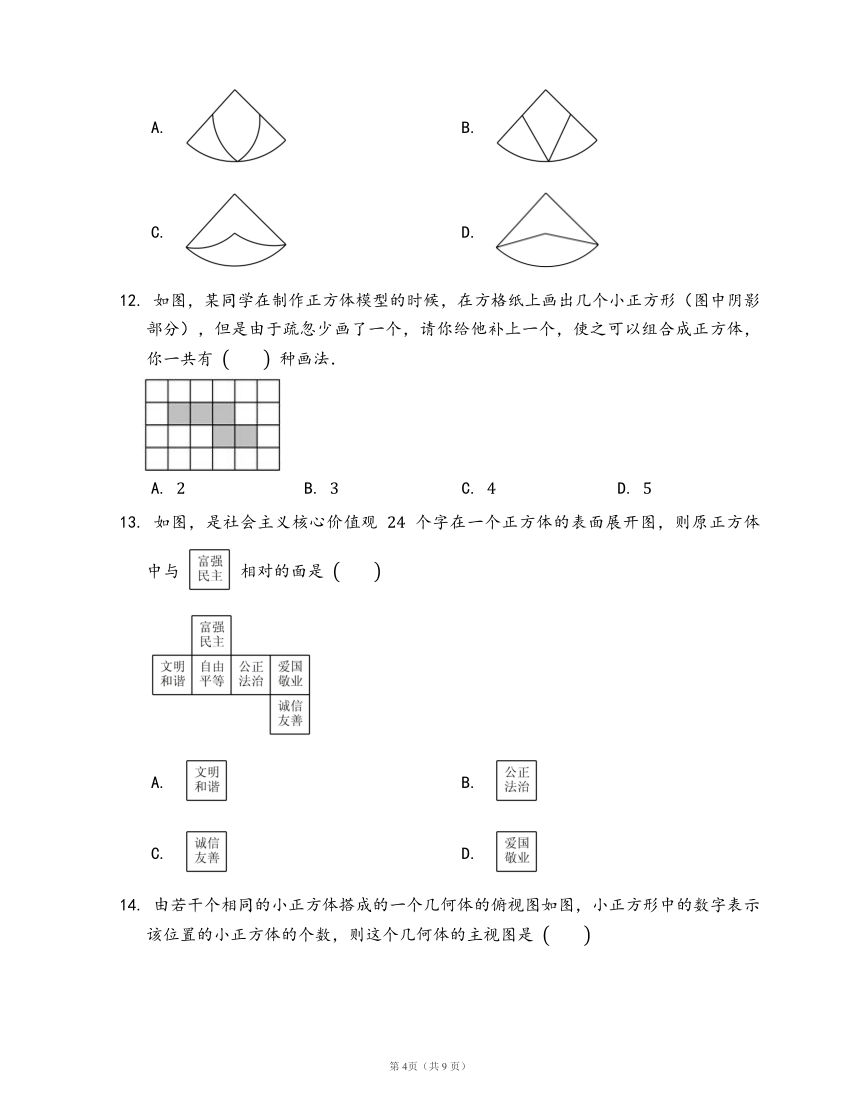
12. 如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有 ?? 种画法.
A. 2 B. 3 C. 4 D. 5
13. 如图,是社会主义核心价值观 24 个字在一个正方体的表面展开图,则原正方体中与相对的面是 ??
A. B.
C. D.
14. 由若干个相同的小正方体搭成的一个几何体的俯视图如图,小正方形中的数字表示该位置的小正方体的个数,则这个几何体的主视图是 ??
A. B.
C. D.
15. 下列图形中,是圆锥的侧面展开图的为 ??
A. B.
C. D.
二、填空题(共5小题;共30分)
16. 如图所示图形是立体图形的表面展开图,说出这些立体图形的名称.
① ?;② ?;③ ?;④ ?.
17. 如图为某几何体的展开图,该几何体的名称是 ?.
18. 设计长方体的包装盒,要先绘制长方体的 ?,再把它剪出并折叠成长方体.此外,还会用到 ? 知识、 ? 知识、 ? 等.
19. 一个几何体的三视图如图所示,其中主视图和俯视图都是矩形,则它的表面积是 ?.
20. 如图,它是一个正方体六个面的展开图,那么原正方体中与平面 B 互相平行的平面是 ?.(用图中字母表示)
三、解答题(共3小题;共45分)
21. 某奶制品厂生产了一批瓶装牛奶(瓶底为圆形),为了便于销售和运输,需要将其按固定数量装入如图 所示的正方体包装箱中.现已在包装箱内装入了 6 瓶牛奶,那么要把包装箱装满还要再装多少瓶?
22. 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
23. 如图所示是一个正方体的表面展开图,把 0,1,2,3,4,5 分别填入 6 个小正方形内,使得按虚线折成正方体后相对的两个面上的数字之和为 5,尝试不同的填法,并与同学交流.
答案
第一部分
1. B
2. A
3. C
4. B
5. B
6. B 【解析】从俯视图可得最底层有 3 个小正方体,
由主视图可得上面一层至少有 1 个小正方体,
所以至少需要 4 个这样的小正方体.
7. D
8. A 【解析】题意分析可知,胶滚上第一行中间为小黑长方形,胶滚从左到右将图案涂到墙上,故第一行应该中间为小黑长方形,所以只有A满足条件.
9. A
10. B
11. B
12. C 【解析】如图所示,共有 4 种画法.
13. C
14. A 【解析】由俯视图中的数字可得:主视图有 4 列,从左到右分别是 1,2,2,1 个正方形.
15. A
【解析】圆锥的侧面展开图是光滑的曲面,没有棱,只是扇形.
第二部分
16. ①长方体(四棱柱)
②三棱柱
③三棱锥
④圆锥
17. 圆柱
18. 展开图,美术,语言,生产常识
19. 108
【解析】几何体为直三菱柱,底为直角三角形.
20. D
第三部分
21. 由图可得 5×5×2-6=44(瓶),
即要把包装箱装满还要再装 44 瓶.
22.
23. (答案不唯一)
一、选择题(共15小题;共75分)
1. 下列图形中,表示立体图形的个数是 ??
A. 2 个 B. 3 个 C. 4 个 D. 5 个
2. 下列图形中可以作为一个三棱柱的展开图的是 ??
A. B.
C. D.
3. 已知 BC 是圆柱底面的直径,AB 是圆柱的高,在圆柱的侧面上,过点 A,C 嵌有一圈路径最短的金属丝,现将圆柱侧面沿 AB 剪开,所得的圆柱的侧面展开图是 ??
A. B.
C. D.
4. 下列图形中,不能经过折叠围成正方体的是 ??
A. B.
C. D.
5. 把右图中的三棱柱展开,所得到的展开图是 ??
A. B.
C. D.
6. 某几何体由一些大小相同的小正方体组成,如图分别是它的主视图和俯视图,那么要组成该几何体,至少需要多少个这样的小正方体 ??
A. 3 B. 4 C. 5 D. 6
7. 小亮将考试时自勉的话"沉稳、细心、规范"写在一个正方体的六个面上,其平面展开图如图所示,那么该正方体中和"稳"字相对的字是 ??
A. 细 B. 心 C. 规 D. 范
8. 小明用如图所示的胶滚从左到右的方向将图案涂到墙上,符合图示胶滚涂出的图案是 ??
A. B.
C. D.
9. 如图,是一个几何体的三视图,则该几何体的展开图为 ??
A. B.
C. D.
10. 如图,是正方体的平面展开图,每个面上都标有一个汉字,与“爱”字对应的面上的字为 ??
A. 顺 B. 义 C. 家 D. 乡
11. 如图,S 是圆锥的顶点,AB 是圆锥底面的直径,M 是 SA 的中点.在圆锥的侧面上过点 B,M 嵌有一圈路径最短的金属丝,现将圆锥侧面沿 SA 剪开,所得圆锥的侧面展开图可能是 ??
A. B.
C. D.
12. 如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有 ?? 种画法.
A. 2 B. 3 C. 4 D. 5
13. 如图,是社会主义核心价值观 24 个字在一个正方体的表面展开图,则原正方体中与相对的面是 ??
A. B.
C. D.
14. 由若干个相同的小正方体搭成的一个几何体的俯视图如图,小正方形中的数字表示该位置的小正方体的个数,则这个几何体的主视图是 ??
A. B.
C. D.
15. 下列图形中,是圆锥的侧面展开图的为 ??
A. B.
C. D.
二、填空题(共5小题;共30分)
16. 如图所示图形是立体图形的表面展开图,说出这些立体图形的名称.
① ?;② ?;③ ?;④ ?.
17. 如图为某几何体的展开图,该几何体的名称是 ?.
18. 设计长方体的包装盒,要先绘制长方体的 ?,再把它剪出并折叠成长方体.此外,还会用到 ? 知识、 ? 知识、 ? 等.
19. 一个几何体的三视图如图所示,其中主视图和俯视图都是矩形,则它的表面积是 ?.
20. 如图,它是一个正方体六个面的展开图,那么原正方体中与平面 B 互相平行的平面是 ?.(用图中字母表示)
三、解答题(共3小题;共45分)
21. 某奶制品厂生产了一批瓶装牛奶(瓶底为圆形),为了便于销售和运输,需要将其按固定数量装入如图 所示的正方体包装箱中.现已在包装箱内装入了 6 瓶牛奶,那么要把包装箱装满还要再装多少瓶?
22. 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
23. 如图所示是一个正方体的表面展开图,把 0,1,2,3,4,5 分别填入 6 个小正方形内,使得按虚线折成正方体后相对的两个面上的数字之和为 5,尝试不同的填法,并与同学交流.
答案
第一部分
1. B
2. A
3. C
4. B
5. B
6. B 【解析】从俯视图可得最底层有 3 个小正方体,
由主视图可得上面一层至少有 1 个小正方体,
所以至少需要 4 个这样的小正方体.
7. D
8. A 【解析】题意分析可知,胶滚上第一行中间为小黑长方形,胶滚从左到右将图案涂到墙上,故第一行应该中间为小黑长方形,所以只有A满足条件.
9. A
10. B
11. B
12. C 【解析】如图所示,共有 4 种画法.
13. C
14. A 【解析】由俯视图中的数字可得:主视图有 4 列,从左到右分别是 1,2,2,1 个正方形.
15. A
【解析】圆锥的侧面展开图是光滑的曲面,没有棱,只是扇形.
第二部分
16. ①长方体(四棱柱)
②三棱柱
③三棱锥
④圆锥
17. 圆柱
18. 展开图,美术,语言,生产常识
19. 108
【解析】几何体为直三菱柱,底为直角三角形.
20. D
第三部分
21. 由图可得 5×5×2-6=44(瓶),
即要把包装箱装满还要再装 44 瓶.
22.
23. (答案不唯一)
