人教版小学数学六年级上册讲义 几何图形的周长和面积(含答案)
文档属性
| 名称 | 人教版小学数学六年级上册讲义 几何图形的周长和面积(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 141.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 00:00:00 | ||
图片预览



文档简介
第十三讲 几何图形的周长+面积
第一部分 【部分面试试题(真题)/ 模拟题展示】考点一:长方形和正方形。
长方形的面积=长×宽,正方形的面积=边长×边长。掌握并能运用这两个面积公式,就能计算它们的面 积。
但是,在平时的学习过程中,我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出面积的题目。这就需要我们切实掌握有关概念,利用“割补”、“平移”、“旋转”等方法, 使复杂的问题转化为普通的求长方形、正方形面积的问题,从而正确解答。
【例 1】把长 130 厘米的铁丝围成一个长方形,接头处重合 2 厘米,要使长比宽多 18 厘米,长和宽各是多少厘米?
1257300643890【例 2】已知大正方形比小正方形边长多 2 厘米,大正方形比小正方形的面积大 40 平方厘米。求大、小正方形的面积各是多少平方厘米?
1287780734060【例 3】把 20 分米长的线段分成两段,并且在每一段上作一正方形,已知两个正方形的面积相差 40 平方分米,大正方形的面积是多少平方分米?
941705541655【例 4】下图是一块长方形草地,长方形的长是 16,宽是 10,中间有两条道路,一条是长方形,一条是平行四边形,那么,有草部分(阴影部分)的面积有多大?(单位:米)
考点二:三角形、梯形的面积
【例 5】一个三角形的底为 5m,如果底延长 1m,那么三角形的面积就增加 1.5 m 2 ,求原来三角形的面积。
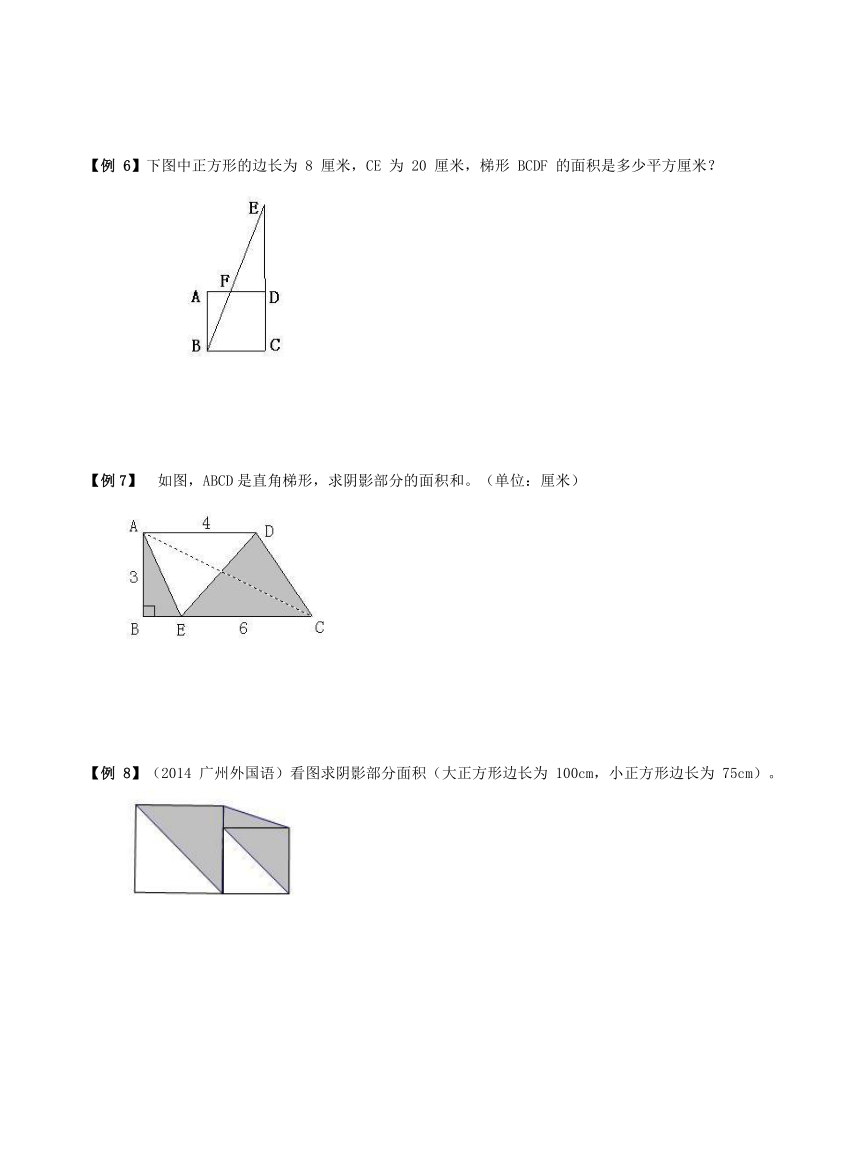
【例 6】下图中正方形的边长为 8 厘米,CE 为 20 厘米,梯形 BCDF 的面积是多少平方厘米?
1587500121920
【例 7】 如图,ABCD 是直角梯形,求阴影部分的面积和。(单位:厘米)
1054100133985
1054100244475【例 8】(2014 广州外国语)看图求阴影部分面积(大正方形边长为 100cm,小正方形边长为 75cm)。
考点三:圆的周长与面积
1587500730885【例 9】一个直径为 20 厘米的大圆内有许多小圆,这些小圆的圆心都在大圆的一个直径上.则小圆的周长之和为 厘米.
1054100541020【例 10】(广州第二外国语学校) 如下图所示,圆形面积是 18.84 平方厘米,圆形内最大的正方形的面积为多少?
考点四:长方体和正方体
【例 11】有一个长方体容器,从里面量长 5 分米、宽 4 分米、高 6 分米,里面注有水,水深 3 分米。如
果把一块边长 2 分米的正方体铁块浸入水中,水面上升多少分米?
【例 12】一个正方体木块,棱长是 3 厘米。如果在这个木块的六个面的中心位置各挖去一个边长为 1 厘米的正方形孔,直透对面。所得立体图形的体积是多少?
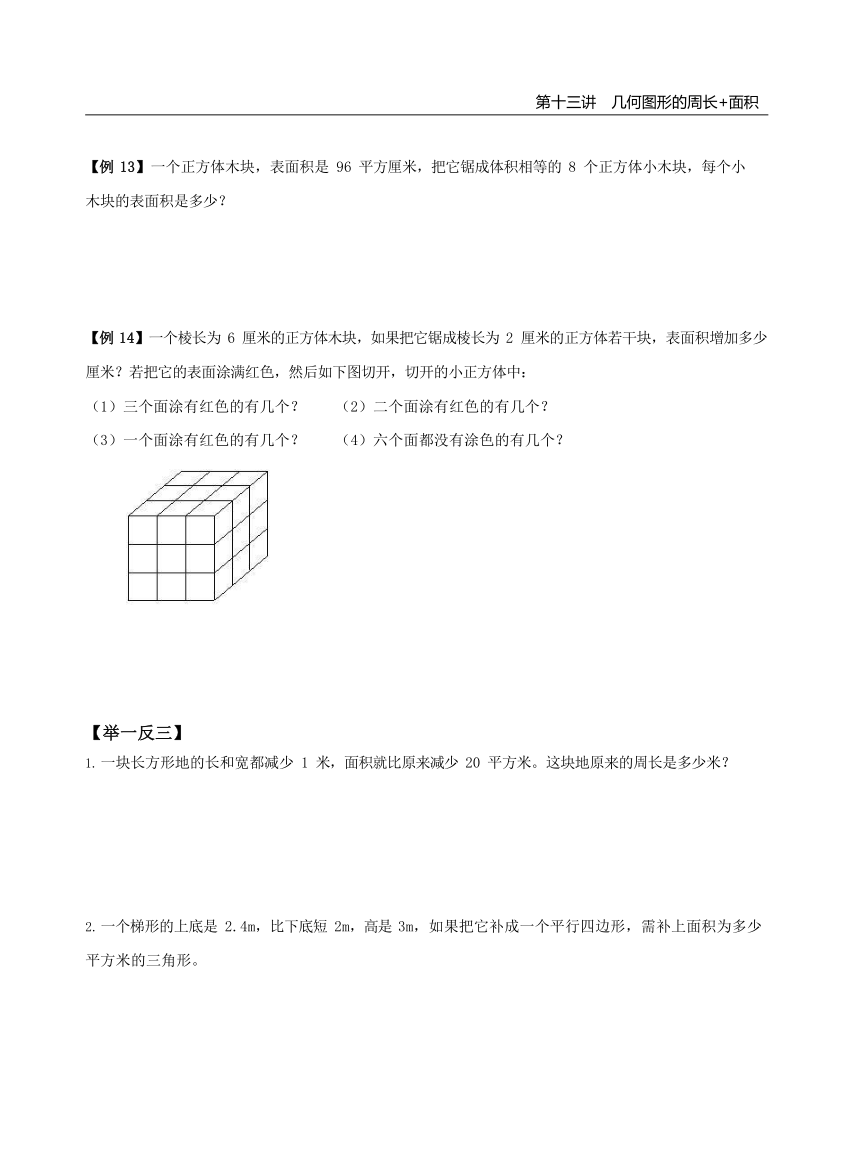
【例 13】一个正方体木块,表面积是 96 平方厘米,把它锯成体积相等的 8 个正方体小木块,每个小木块的表面积是多少?
【例 14】一个棱长为 6 厘米的正方体木块,如果把它锯成棱长为 2 厘米的正方体若干块,表面积增加多少厘米?若把它的表面涂满红色,然后如下图切开,切开的小正方体中:
(1)三个面涂有红色的有几个? (2)二个面涂有红色的有几个?
(3)一个面涂有红色的有几个? (4)六个面都没有涂色的有几个?
1054100109855
【举一反三】
一块长方形地的长和宽都减少 1 米,面积就比原来减少 20 平方米。这块地原来的周长是多少米?
一个梯形的上底是 2.4m,比下底短 2m,高是 3m,如果把它补成一个平行四边形,需补上面积为多少平方米的三角形。
一个长方体的木块,长 8 分米,宽 4 分米,高 2 分米。把它锯成若干个小正方体,然后再拼成一个大正方体。这个大正方体的表面积是多少平方分米
求下图长方形 ABCD 的面积(单位:厘米)。
1054100101600
如下图,正方形 ABCD 中,AB=4 厘米,EC=10 厘米,求阴影部分的面积。
132080099060
1054100615950下图中,三角形 ABC 的面积是 36 平方厘米,三角形 ABE 与三角形 AEC 的面积相等,如果 AB=9 厘米, FB=FE,求三角形 AFE 的面积。
两条对角线把梯形 ABCD 分割成四个三角形。已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)
有两种自然的放法将正方形内接于等腰直角三角形。已知等腰直角三角形的面积是 36 平方厘米,两个正方形的面积分别是多少?
1148715624205下图是一块长方形草地,长方形长为 16,宽为 12,中间有一条宽为 2 的道路,求草地(阴影部分) 的面积。
882015579120右图中三角形 ABC 为等边三角形,D 为 AB 边上的中点。已知三角形 BDE 的面积为 5 平方厘米。求等边三角形 ABC 的面积。
882015636270下图表示一个正方体,它的棱长为 4cm,在它的上下、前后、左右的正中位置各挖去一个棱长为 1cm 的正方体,问:此图的表面积是多少?
1016000484505如右图所示,圆锥形容器中装有 5 升水,水面高度正好是圆锥高度的一半,这个容器还能装多少升水?
第十三讲 【答案】
考点一:长方形和正方形。
长方形的面积=长×宽,正方形的面积=边长×边长。掌握并能运用这两个面积公式,就能计算它们的面 积。
但是,在平时的学习过程中,我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出面积的题目。这就需要我们切实掌握有关概念,利用“割补”、“平移”、“旋转”等方法, 使复杂的问题转化为普通的求长方形、正方形面积的问题,从而正确解答。
【例 1】把长 130 厘米的铁丝围成一个长方形,接头处重合 2 厘米,要使长比宽多 18 厘米,长和宽各是多少厘米?
【知识点】长方形的周长,和差问题。
【答案】长为 41 厘米,宽为 23 厘米。
【解析】围成的长方形周长为 130-2=128 厘米,长与宽的和为 64 厘米,根据和差问题的公式,长为(64+18)
÷2=41 厘米,宽为(64-18)÷2=2 厘米。
【点评】文字题,空间想象力是关键。
1257300741045【例 2】已知大正方形比小正方形边长多 2 厘米,大正方形比小正方形的面积大 40 平方厘米。求大、小正方形的面积各是多少平方厘米?
【知识点】正方形的面积公式。
【答案】小正方形的面积为 81 平方厘米,大正方形面积为 121 平方厘米。
【解析】从图中可以看出,大正方形的面积比小正方形的面积大出的 40 平方厘米,可以分成三部分,其中 A 和 B 的面积相等。因此,用 40 平方厘米减去阴影部分的面积,再除以 2 就能得到长方形 A 和 B 的面积,再用 A 或 B 的面积除以 2 就是小正方形的边长。求出了小正方形的边长,计算大、小正方形的面积就非常简单了。
【点评】这类题目要求对正方形的面积公式非常熟练并能灵活运用。
1238885719455【例 3】把 20 分米长的线段分成两段,并且在每一段上作一正方形,已知两个正方形的面积相差 40 平方分米,大正方形的面积是多少平方分米?
【知识点】 正方形、长方形的面积公式及和差问题的公式。
【答案】大正方形面积为 121 平方分米。
【解析】我们可以把小正方形移至大正方形里面进行分析。两个正方形的面积差 40 平方分米就是图中的A 和 B 两部分,如图。如果把 B 移到原来小正方形的上面,不难看出,A 和 B 正好组成一个长方形,此长方形的面积是 40 平方分米,长 20 分米,宽是 40÷20=2(分米),即大、小两个正方形的边长相差 2 分米。因此,大正方形的边长就是(20+2)÷2=11(分米),面积是 11×11=121(平方分米)。
【点评】这类题目是正方形、长方形的面积公式及和差问题的综合应用题,难度较大,作为面试题,可用试数法。
975360544195【例 4】下图是一块长方形草地,长方形的长是 16,宽是 10,中间有两条道路,一条是长方形,一条是平行四边形,那么,有草部分(阴影部分)的面积有多大?(单位:米)
【知识点】平行四边形的面积,等面积转化法。
【答案】阴影部分的面积为 112 平方米。
【解析】把长方形进行平移,平行四边形变成等底等高的长方形,然后平移,阴影部分变为一个长 14
米,宽 8 米的长方形。所以 14×8=112 平方米。
【点评】这类题目重点考察转化法,计算很简单。
考点二:三角形、梯形的面积
【例 5】一个三角形的底为 5m,如果底延长 1m,那么三角形的面积就增加 1.5 m 2 ,求原来三角形的面积。
【知识点】三角形的面积。
【答案】原来三角形的面积为 7.5 平方米。
【解析】底为 5 厘米和底为 1 厘米的三角形同高,所以原来三角形的面积是 1.5 的 5 倍,即 7.5 平方米。
【点评】能想象出图形是关键。
【例 6】下图中正方形的边长为 8 厘米,CE 为 20 厘米,梯形 BCDF 的面积是多少平方厘米?
1587500118745
【知识点】三角形、梯形、正方形组合图形题
【答案】梯形的面积为 51.2 平方厘米。
【解析】要求梯形的面积,关键是要求出上底 FD 的长度。
连接FC 后就能得到一个三角形 EFC,用三角形 EBC 的面积减去三角形 FBC 的面积就能得到三角形 EFC 的面积:8×20÷2-8×8÷2=48 平方厘米。
FD=48×2÷20=4.8 厘米,
所求梯形的面积就是(4.8+8)×8÷2=51.2 平方厘米。
【点评】本题的难点是作辅助线 FC 从而才能求出 FD 的长度。
【例 7】 如图,ABCD 是直角梯形,求阴影部分的面积和。(单位:厘米)
【知识点】三角形的面积巧算题
【答案】阴影部分面积和为 9 平方厘米。
【解析】按照一般解法,首先要求出梯形的面积,然后减去空白部分的面积即得所求面积。其实,只要连接AC,显然三角形 AEC 与三角形 DEC 同底等高其面积相等,这样,我们把两个阴影部分合成了一个三角形 ABC。面积是:6×3÷2=9 平方厘米。
【点评】本题的难点是灵活运用等底等高的两个三角形的面积相等。
1054100338455【例 8】(2014 广州外国语)看图求阴影部分面积(大正方形边长为 100cm,小正方形边长为 75cm)。
【知识点】长方形面积。
【答案】面积是 3750cm?.
949325240665【解析】如下图:左边是正方形面积的一半为 5000cm?,右边底为 100cm,高是 75cm,面积是 3750cm?。
【点评】一半模型要牢记,面积的巧算。
考点三:圆的周长与面积
1520825614045【例 9】一个直径为 20 厘米的大圆内有许多小圆,这些小圆的圆心都在大圆的一个直径上.则小圆的周长之和为 厘米.
【知识点】圆的周长的计算
【答案】62.8 厘米。
【解析】小圆的周长之和等于大圆的周长,所以直接计算大圆的周长即可。3.14×20=62.8 厘米。
【点评】本题属于较复杂的圆的周长的计算问题。解决本题的关键是所有小圆的直径都在大圆的直径上, 即所有小圆的直径之和等于大圆的直径,理解这一点,问题就解决了。
1054100541020【例 10】(广州第二外国语学校) 如下图所示,圆形面积是 18.84 平方厘米,圆形内最大的正方形的面积为多少?
【知识点】圆中最大正方形面积与圆面积之比。
【解析】S 圆:S 正=π:2
S 正=18.84÷3.14×2=12 平方厘米。
【点评】圆中最大正方形面积与圆面积之比是π:2。
考点四:长方体和正方体
【例 11】有一个长方体容器,从里面量长 5 分米、宽 4 分米、高 6 分米,里面注有水,水深 3 分米。如
果把一块边长 2 分米的正方体铁块浸入水中,水面上升多少分米?
【知识点】长方体和正方体的体积。
【答案】水面上升了 0.4 分米。
【解析】(铁块的体积是 2×2×2=8(立方分米),把它浸入水中后,它就占了 8 立方分米的空间,因此,水上升的体积也就是 8 立方分米,用这个体积除以底面积(5×4)就能得到水上升的高度了。
【点评】这类问题要能够掌握长方体和正方体的体积=底面积×高这个公式。
【例 12】一个正方体木块,棱长是 3 厘米。如果在这个木块的六个面的中心位置各挖去一个边长为 1 厘米的正方形孔,直透对面。所得立体图形的体积是多少?
【知识点】长方体和正方体的体积。
【答案】所得立体图形的体积为 20 立方厘米。
【解析】原来正方体体积为 3×3×3=27 立方厘米,挖去的体积为 3×1×3-2=7 立方厘米,剩下 27-7=20 立方厘米。
【点评】想象出图形是关键。
【例 13】一个正方体木块,表面积是 96 平方厘米,把它锯成体积相等的 8 个正方体小木块,每个小木块的表面积是多少?
【知识点】正方体的表面积.
【答案】每个小木块的表面积为 24 平方厘米。
【解析】据成 8 个小正方体木块,即二阶魔方。所以小正方块每个面的面积为 96÷6÷4=4 平方厘米,表
面积为 4×6=24 平方厘米。
【点评】解决这个问题关键想象出如何切的,要有整体思想,不必求棱长。
【例 14】一个棱长为 6 厘米的正方体木块,如果把它锯成棱长为 2 厘米的正方体若干块,表面积增加多少厘米?若把它的表面涂满红色,然后如下图切开,切开的小正方体中:
(1)三个面涂有红色的有几个? (2)二个面涂有红色的有几个?
一个面涂有红色的有几个? (4)六个面都没有涂色的有几个?
【知识点】正方体的表面积;
【答案】表面积增加 432 平方厘米。
【解析】把棱长为 6 厘米的正方体锯成棱长为 2 厘米的正方体,可以按下图中的线共锯 6 次,每锯一次
就增加两个 6×6=36 平方厘米的面,锯 6 次共增加 36×2×6=432 平方厘米的面积。因此,锯好后表面积
增加 432 平方厘米。
按题中的要求切,切成的小正方体一共有 3×3×3=27 个。
三个面涂有红色的小正方体在大正方体的顶点处,共有 8 个;
二个面涂有红色的小正方体在大正方体的棱上,共有 1×12=12 个;
一个面涂有红色的小正方体在大正方体的六个面上,共有 1×6=6 个;
六个面都没有涂色的在大正方体的中间,有 27-(8+12+6)=1 个。
【点评】这类问题要掌握好切割正方体表面积增加的规律,要有整体思想。
【举一反三】答案:
1、 42 米。 2、3 平方米 3、96 平方分米
4、48 平方厘米。 5、 3.2 平方厘米。 6、 10 平方厘米。
7、 因为三角形 ABD 与三角形 ACD 等底等高,所以面积相等。因此,三角形 ABO 的面积和三角形 DOC 的面积相等,也是 6 平方厘米。因为三角形 BOC 的面积是三角形 DOC 面积的 2 倍,所以 BO 的长度是 OD 的2 倍,即三角形 ABO 的面积也是三角形 AOD 的 2 倍。所以,三角形 AOD 的面积是 6÷2=3 平方厘米。
8、 分别为 18 平方厘米和 16 平方厘米。
9、140 平方米。
10、40 平方厘米。
11、120 平方厘米。
12、35 升
第一部分 【部分面试试题(真题)/ 模拟题展示】考点一:长方形和正方形。
长方形的面积=长×宽,正方形的面积=边长×边长。掌握并能运用这两个面积公式,就能计算它们的面 积。
但是,在平时的学习过程中,我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出面积的题目。这就需要我们切实掌握有关概念,利用“割补”、“平移”、“旋转”等方法, 使复杂的问题转化为普通的求长方形、正方形面积的问题,从而正确解答。
【例 1】把长 130 厘米的铁丝围成一个长方形,接头处重合 2 厘米,要使长比宽多 18 厘米,长和宽各是多少厘米?
1257300643890【例 2】已知大正方形比小正方形边长多 2 厘米,大正方形比小正方形的面积大 40 平方厘米。求大、小正方形的面积各是多少平方厘米?
1287780734060【例 3】把 20 分米长的线段分成两段,并且在每一段上作一正方形,已知两个正方形的面积相差 40 平方分米,大正方形的面积是多少平方分米?
941705541655【例 4】下图是一块长方形草地,长方形的长是 16,宽是 10,中间有两条道路,一条是长方形,一条是平行四边形,那么,有草部分(阴影部分)的面积有多大?(单位:米)
考点二:三角形、梯形的面积
【例 5】一个三角形的底为 5m,如果底延长 1m,那么三角形的面积就增加 1.5 m 2 ,求原来三角形的面积。
【例 6】下图中正方形的边长为 8 厘米,CE 为 20 厘米,梯形 BCDF 的面积是多少平方厘米?
1587500121920
【例 7】 如图,ABCD 是直角梯形,求阴影部分的面积和。(单位:厘米)
1054100133985
1054100244475【例 8】(2014 广州外国语)看图求阴影部分面积(大正方形边长为 100cm,小正方形边长为 75cm)。
考点三:圆的周长与面积
1587500730885【例 9】一个直径为 20 厘米的大圆内有许多小圆,这些小圆的圆心都在大圆的一个直径上.则小圆的周长之和为 厘米.
1054100541020【例 10】(广州第二外国语学校) 如下图所示,圆形面积是 18.84 平方厘米,圆形内最大的正方形的面积为多少?
考点四:长方体和正方体
【例 11】有一个长方体容器,从里面量长 5 分米、宽 4 分米、高 6 分米,里面注有水,水深 3 分米。如
果把一块边长 2 分米的正方体铁块浸入水中,水面上升多少分米?
【例 12】一个正方体木块,棱长是 3 厘米。如果在这个木块的六个面的中心位置各挖去一个边长为 1 厘米的正方形孔,直透对面。所得立体图形的体积是多少?
【例 13】一个正方体木块,表面积是 96 平方厘米,把它锯成体积相等的 8 个正方体小木块,每个小木块的表面积是多少?
【例 14】一个棱长为 6 厘米的正方体木块,如果把它锯成棱长为 2 厘米的正方体若干块,表面积增加多少厘米?若把它的表面涂满红色,然后如下图切开,切开的小正方体中:
(1)三个面涂有红色的有几个? (2)二个面涂有红色的有几个?
(3)一个面涂有红色的有几个? (4)六个面都没有涂色的有几个?
1054100109855
【举一反三】
一块长方形地的长和宽都减少 1 米,面积就比原来减少 20 平方米。这块地原来的周长是多少米?
一个梯形的上底是 2.4m,比下底短 2m,高是 3m,如果把它补成一个平行四边形,需补上面积为多少平方米的三角形。
一个长方体的木块,长 8 分米,宽 4 分米,高 2 分米。把它锯成若干个小正方体,然后再拼成一个大正方体。这个大正方体的表面积是多少平方分米
求下图长方形 ABCD 的面积(单位:厘米)。
1054100101600
如下图,正方形 ABCD 中,AB=4 厘米,EC=10 厘米,求阴影部分的面积。
132080099060
1054100615950下图中,三角形 ABC 的面积是 36 平方厘米,三角形 ABE 与三角形 AEC 的面积相等,如果 AB=9 厘米, FB=FE,求三角形 AFE 的面积。
两条对角线把梯形 ABCD 分割成四个三角形。已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)
有两种自然的放法将正方形内接于等腰直角三角形。已知等腰直角三角形的面积是 36 平方厘米,两个正方形的面积分别是多少?
1148715624205下图是一块长方形草地,长方形长为 16,宽为 12,中间有一条宽为 2 的道路,求草地(阴影部分) 的面积。
882015579120右图中三角形 ABC 为等边三角形,D 为 AB 边上的中点。已知三角形 BDE 的面积为 5 平方厘米。求等边三角形 ABC 的面积。
882015636270下图表示一个正方体,它的棱长为 4cm,在它的上下、前后、左右的正中位置各挖去一个棱长为 1cm 的正方体,问:此图的表面积是多少?
1016000484505如右图所示,圆锥形容器中装有 5 升水,水面高度正好是圆锥高度的一半,这个容器还能装多少升水?
第十三讲 【答案】
考点一:长方形和正方形。
长方形的面积=长×宽,正方形的面积=边长×边长。掌握并能运用这两个面积公式,就能计算它们的面 积。
但是,在平时的学习过程中,我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出面积的题目。这就需要我们切实掌握有关概念,利用“割补”、“平移”、“旋转”等方法, 使复杂的问题转化为普通的求长方形、正方形面积的问题,从而正确解答。
【例 1】把长 130 厘米的铁丝围成一个长方形,接头处重合 2 厘米,要使长比宽多 18 厘米,长和宽各是多少厘米?
【知识点】长方形的周长,和差问题。
【答案】长为 41 厘米,宽为 23 厘米。
【解析】围成的长方形周长为 130-2=128 厘米,长与宽的和为 64 厘米,根据和差问题的公式,长为(64+18)
÷2=41 厘米,宽为(64-18)÷2=2 厘米。
【点评】文字题,空间想象力是关键。
1257300741045【例 2】已知大正方形比小正方形边长多 2 厘米,大正方形比小正方形的面积大 40 平方厘米。求大、小正方形的面积各是多少平方厘米?
【知识点】正方形的面积公式。
【答案】小正方形的面积为 81 平方厘米,大正方形面积为 121 平方厘米。
【解析】从图中可以看出,大正方形的面积比小正方形的面积大出的 40 平方厘米,可以分成三部分,其中 A 和 B 的面积相等。因此,用 40 平方厘米减去阴影部分的面积,再除以 2 就能得到长方形 A 和 B 的面积,再用 A 或 B 的面积除以 2 就是小正方形的边长。求出了小正方形的边长,计算大、小正方形的面积就非常简单了。
【点评】这类题目要求对正方形的面积公式非常熟练并能灵活运用。
1238885719455【例 3】把 20 分米长的线段分成两段,并且在每一段上作一正方形,已知两个正方形的面积相差 40 平方分米,大正方形的面积是多少平方分米?
【知识点】 正方形、长方形的面积公式及和差问题的公式。
【答案】大正方形面积为 121 平方分米。
【解析】我们可以把小正方形移至大正方形里面进行分析。两个正方形的面积差 40 平方分米就是图中的A 和 B 两部分,如图。如果把 B 移到原来小正方形的上面,不难看出,A 和 B 正好组成一个长方形,此长方形的面积是 40 平方分米,长 20 分米,宽是 40÷20=2(分米),即大、小两个正方形的边长相差 2 分米。因此,大正方形的边长就是(20+2)÷2=11(分米),面积是 11×11=121(平方分米)。
【点评】这类题目是正方形、长方形的面积公式及和差问题的综合应用题,难度较大,作为面试题,可用试数法。
975360544195【例 4】下图是一块长方形草地,长方形的长是 16,宽是 10,中间有两条道路,一条是长方形,一条是平行四边形,那么,有草部分(阴影部分)的面积有多大?(单位:米)
【知识点】平行四边形的面积,等面积转化法。
【答案】阴影部分的面积为 112 平方米。
【解析】把长方形进行平移,平行四边形变成等底等高的长方形,然后平移,阴影部分变为一个长 14
米,宽 8 米的长方形。所以 14×8=112 平方米。
【点评】这类题目重点考察转化法,计算很简单。
考点二:三角形、梯形的面积
【例 5】一个三角形的底为 5m,如果底延长 1m,那么三角形的面积就增加 1.5 m 2 ,求原来三角形的面积。
【知识点】三角形的面积。
【答案】原来三角形的面积为 7.5 平方米。
【解析】底为 5 厘米和底为 1 厘米的三角形同高,所以原来三角形的面积是 1.5 的 5 倍,即 7.5 平方米。
【点评】能想象出图形是关键。
【例 6】下图中正方形的边长为 8 厘米,CE 为 20 厘米,梯形 BCDF 的面积是多少平方厘米?
1587500118745
【知识点】三角形、梯形、正方形组合图形题
【答案】梯形的面积为 51.2 平方厘米。
【解析】要求梯形的面积,关键是要求出上底 FD 的长度。
连接FC 后就能得到一个三角形 EFC,用三角形 EBC 的面积减去三角形 FBC 的面积就能得到三角形 EFC 的面积:8×20÷2-8×8÷2=48 平方厘米。
FD=48×2÷20=4.8 厘米,
所求梯形的面积就是(4.8+8)×8÷2=51.2 平方厘米。
【点评】本题的难点是作辅助线 FC 从而才能求出 FD 的长度。
【例 7】 如图,ABCD 是直角梯形,求阴影部分的面积和。(单位:厘米)
【知识点】三角形的面积巧算题
【答案】阴影部分面积和为 9 平方厘米。
【解析】按照一般解法,首先要求出梯形的面积,然后减去空白部分的面积即得所求面积。其实,只要连接AC,显然三角形 AEC 与三角形 DEC 同底等高其面积相等,这样,我们把两个阴影部分合成了一个三角形 ABC。面积是:6×3÷2=9 平方厘米。
【点评】本题的难点是灵活运用等底等高的两个三角形的面积相等。
1054100338455【例 8】(2014 广州外国语)看图求阴影部分面积(大正方形边长为 100cm,小正方形边长为 75cm)。
【知识点】长方形面积。
【答案】面积是 3750cm?.
949325240665【解析】如下图:左边是正方形面积的一半为 5000cm?,右边底为 100cm,高是 75cm,面积是 3750cm?。
【点评】一半模型要牢记,面积的巧算。
考点三:圆的周长与面积
1520825614045【例 9】一个直径为 20 厘米的大圆内有许多小圆,这些小圆的圆心都在大圆的一个直径上.则小圆的周长之和为 厘米.
【知识点】圆的周长的计算
【答案】62.8 厘米。
【解析】小圆的周长之和等于大圆的周长,所以直接计算大圆的周长即可。3.14×20=62.8 厘米。
【点评】本题属于较复杂的圆的周长的计算问题。解决本题的关键是所有小圆的直径都在大圆的直径上, 即所有小圆的直径之和等于大圆的直径,理解这一点,问题就解决了。
1054100541020【例 10】(广州第二外国语学校) 如下图所示,圆形面积是 18.84 平方厘米,圆形内最大的正方形的面积为多少?
【知识点】圆中最大正方形面积与圆面积之比。
【解析】S 圆:S 正=π:2
S 正=18.84÷3.14×2=12 平方厘米。
【点评】圆中最大正方形面积与圆面积之比是π:2。
考点四:长方体和正方体
【例 11】有一个长方体容器,从里面量长 5 分米、宽 4 分米、高 6 分米,里面注有水,水深 3 分米。如
果把一块边长 2 分米的正方体铁块浸入水中,水面上升多少分米?
【知识点】长方体和正方体的体积。
【答案】水面上升了 0.4 分米。
【解析】(铁块的体积是 2×2×2=8(立方分米),把它浸入水中后,它就占了 8 立方分米的空间,因此,水上升的体积也就是 8 立方分米,用这个体积除以底面积(5×4)就能得到水上升的高度了。
【点评】这类问题要能够掌握长方体和正方体的体积=底面积×高这个公式。
【例 12】一个正方体木块,棱长是 3 厘米。如果在这个木块的六个面的中心位置各挖去一个边长为 1 厘米的正方形孔,直透对面。所得立体图形的体积是多少?
【知识点】长方体和正方体的体积。
【答案】所得立体图形的体积为 20 立方厘米。
【解析】原来正方体体积为 3×3×3=27 立方厘米,挖去的体积为 3×1×3-2=7 立方厘米,剩下 27-7=20 立方厘米。
【点评】想象出图形是关键。
【例 13】一个正方体木块,表面积是 96 平方厘米,把它锯成体积相等的 8 个正方体小木块,每个小木块的表面积是多少?
【知识点】正方体的表面积.
【答案】每个小木块的表面积为 24 平方厘米。
【解析】据成 8 个小正方体木块,即二阶魔方。所以小正方块每个面的面积为 96÷6÷4=4 平方厘米,表
面积为 4×6=24 平方厘米。
【点评】解决这个问题关键想象出如何切的,要有整体思想,不必求棱长。
【例 14】一个棱长为 6 厘米的正方体木块,如果把它锯成棱长为 2 厘米的正方体若干块,表面积增加多少厘米?若把它的表面涂满红色,然后如下图切开,切开的小正方体中:
(1)三个面涂有红色的有几个? (2)二个面涂有红色的有几个?
一个面涂有红色的有几个? (4)六个面都没有涂色的有几个?
【知识点】正方体的表面积;
【答案】表面积增加 432 平方厘米。
【解析】把棱长为 6 厘米的正方体锯成棱长为 2 厘米的正方体,可以按下图中的线共锯 6 次,每锯一次
就增加两个 6×6=36 平方厘米的面,锯 6 次共增加 36×2×6=432 平方厘米的面积。因此,锯好后表面积
增加 432 平方厘米。
按题中的要求切,切成的小正方体一共有 3×3×3=27 个。
三个面涂有红色的小正方体在大正方体的顶点处,共有 8 个;
二个面涂有红色的小正方体在大正方体的棱上,共有 1×12=12 个;
一个面涂有红色的小正方体在大正方体的六个面上,共有 1×6=6 个;
六个面都没有涂色的在大正方体的中间,有 27-(8+12+6)=1 个。
【点评】这类问题要掌握好切割正方体表面积增加的规律,要有整体思想。
【举一反三】答案:
1、 42 米。 2、3 平方米 3、96 平方分米
4、48 平方厘米。 5、 3.2 平方厘米。 6、 10 平方厘米。
7、 因为三角形 ABD 与三角形 ACD 等底等高,所以面积相等。因此,三角形 ABO 的面积和三角形 DOC 的面积相等,也是 6 平方厘米。因为三角形 BOC 的面积是三角形 DOC 面积的 2 倍,所以 BO 的长度是 OD 的2 倍,即三角形 ABO 的面积也是三角形 AOD 的 2 倍。所以,三角形 AOD 的面积是 6÷2=3 平方厘米。
8、 分别为 18 平方厘米和 16 平方厘米。
9、140 平方米。
10、40 平方厘米。
11、120 平方厘米。
12、35 升
