江苏省扬州市邗江区蒋王中学2021届高三上学期学情检测数学试卷 Word版含答案
文档属性
| 名称 | 江苏省扬州市邗江区蒋王中学2021届高三上学期学情检测数学试卷 Word版含答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 00:00:00 | ||
图片预览





文档简介
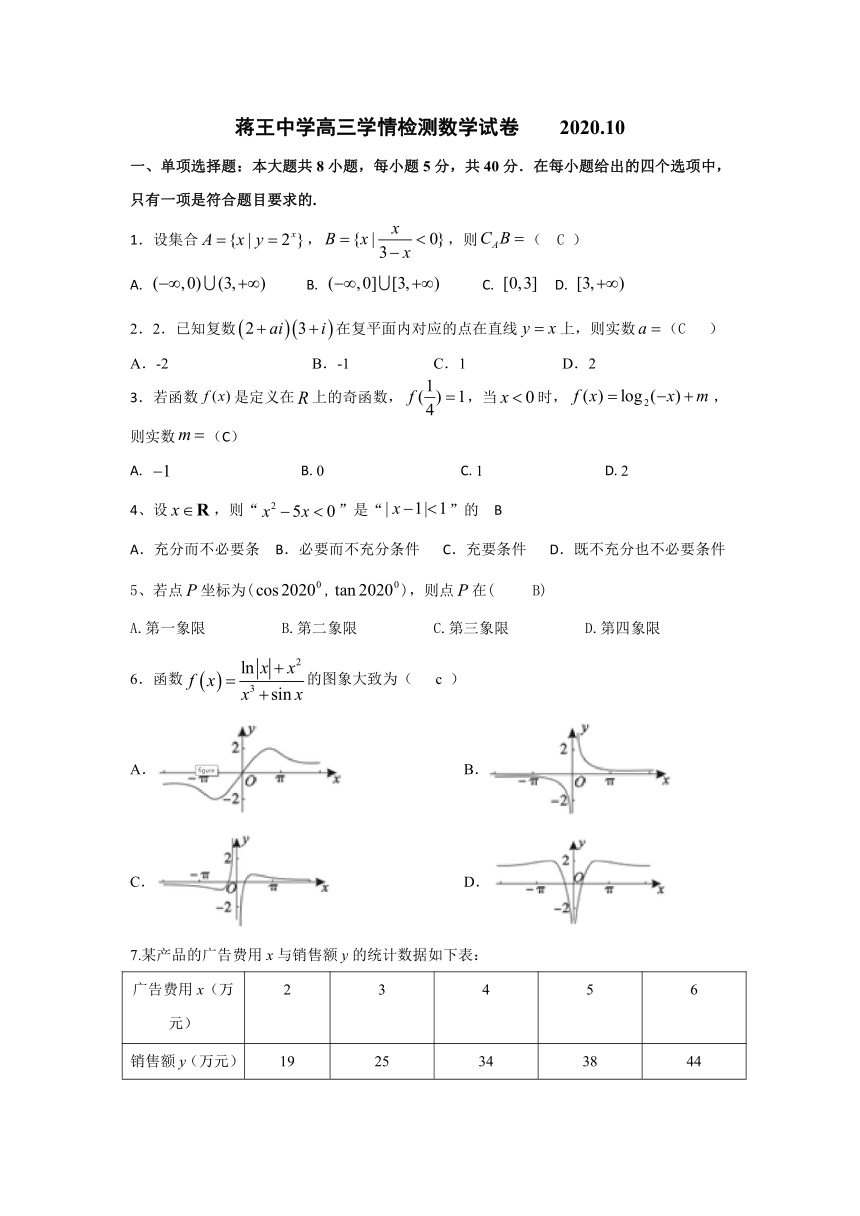
蒋王中学高三学情检测数学试卷 2020.10
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( C )
A. B. C. D.
2.2.已知复数在复平面内对应的点在直线上,则实数(C )
A.-2 B.-1 C.1 D.2
3.若函数是定义在上的奇函数,,当时,,则实数(C)
A. B. 0 C. 1 D. 2
4、设,则“”是“”的 B
A.充分而不必要条 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
5、若点坐标为(,),则点在(? ?B)
A.第一象限?????B.第二象限?????C.第三象限?????D.第四象限
6.函数的图象大致为( c )
A. B.
C. D.
7.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) 2 3 4 5 6
销售额y(万元) 19 25 34 38 44
根据上表可得回归直线方程为,下列说法正确的是( D )
A.回归直线必经过样本点、
B.这组数据的样本中心点未必在回归直线上
C.回归系数6.3的含义是广告费用每增加1万元,销售额实际增加6.3万元
D.据此模型预报广告费用为7万元时销售额为50.9万元
8.已知函数f(x)=-x2+,g(x)=x2ex,若对任意的x2∈[-1,1],存在唯一的x1∈,使得f(x1)=g(x2),则实数a的取值范围是(B)
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.
9.若,,且,则下列不等式恒成立的是( )CD.
A. B. C. D.
10.下列判断正确的是( )BCD
A.已知直线平面,直线平面,则“”是“”的必要不充分条件;
B.若随机变量服从正态分布,,则;
C.若随机变量服从二项分布:,则;
D.是的充分不必要条件.
11.如图是2018年10月—2019年10月中国钢铁同比增速及日均产量统计图,则下列陈述中正确的是( )ABD
A.2019年6月同比增速最大;
B.2019年3月—5月同比增速平稳;
C.2019年8月钢材总产量比2019年9月钢材总产量低;
D.2019年10月钢材总产量约10264万吨。
12.设函数,,给定下列命题,其中是正确命题的是( )ACD
A.不等式的解集为;
B.函数在单调递增,在单调递减;
C.若,则当时,有;
D.若函数有两个极值点,则实数
三、填空题:本题共4小题,每小题5分,共20分.
13.函数在点处的切线与直线垂直,则 .
14.如果的展开式中各项系数之和为4096,则展开式中x的系数为____1215____.
15.函数(,且)的图象恒过定点,且点在角的终边上,则=
16.一圆柱形封闭容器内有一个棱长为2的正四面体,若该正四面体可以绕其中心在容器内任意转动(正四面体顶点恰好触碰到容器内壁可视为可以转动),则容器体积的最小值为
答案
一、选择题答案:
C;2、C;3、C;4、B;5、B;6、C;7、D;8、B
CD;10、BCD;11、ABD;12、ACD
填空题答案:
13、;14、1215;15、;16、
解答题答案:
17、【本题满分10分】
在①AB=A,②AB≠,③BA这三个条件中任选一个,补充在下面问题中,若问题中的实数a存在,求a的取值范围;若不存在,说明理由.
问题:已知集合A=,B=,是否存在实数a,使得 ?
注:如果选择多个条件分别解答,按第一个解答计分.
18.【本题满分12分,】
设函数
(1)若函数y=f(x)的图象关于原点对称,求函数的零点;
(2)若函数在的最大值为-2,求实数a的值.
19、【本题满分12分,】
销售甲种商品所得利润是P万元,它与投入资金t万元的关系有经验公式P=,销售乙种商品所得利润是Q万元,它与投入资金t万元的关系有经验公式Q=bt,其中a,b为常数.现将3万元资金全部投入甲、乙两种商品的销售:若全部投入甲种商品,所得利润为万元;若全部投入乙种商品,所得利润为1万元.若将3万元资金中的x万元投入甲种商品的销售,余下的投入乙种商品的销售,则所得利润总和为f (x)万元.
(1)求函数f (x) 的解析式;
(2)怎样将3万元资金分配给甲、乙两种商品,才能使所得利润总和最大,并求最大值.
2、解:(1)由题意,P=,Q=bt,
故当t=3时,P==,Q=3b=1. …………………… 3分
解得 a=3,b=. …………………… 5分
所以 P=,Q=t.
从而 f(x)=+,x∈[0,3]. ……………………6分
(2)由(1)可得:f(x)=+=-(+).
…………………… 8分
因为x∈[0,3],所以x+1∈[1,4],
故 +≥2,
从而 f(x)≤-2=. …………………… 10分
当且仅当=,即x=2时取等号.
所以f(x)的最大值为 .
答:分别投入2万元、1万元销售甲、乙两种商品时,所得利润总和最大,最大利润是万元. …………………… 12分
20.【本题满分12分,】
如图,在四棱锥中,底面,,,,,是的中点.
(1)求证:平面;
(2)求二面角的余弦值.
20.解:(1)如图,取的中点,连接,.
∵,分别为,的中点,∴,
又且,∴,∴四边形为平行四边形,
∴,又平面,平面,∴平面.
(2)由题意知:,,两两垂直,以为坐标原点,,,所在的直线分别为轴、轴、轴建立如图所示的空间直角坐标系:
∵,分别为,的中点,∴,
又且,∴,∴四边形为平行四边形,
∴,又平面,平面,∴平面.
(2)由题意知:,,两两垂直,以为坐标原点,,,所在的直线分别为轴、轴、轴建立如图所示的空间直角坐标系:
则,,,,,
∴,,,
设平面的法向量,
则,令,则,,∴.
∵平面,∴为平面的一个法向量,
∴,
∵二面角为锐二面角,∴二面角的余弦值为.
21.(12分)《中国制造2025》是经国务院总理李克强签批,由国务院于2015年5月印发的部署全面推进实施制造强国的战略文件,是中国实施制造强国战略第一个十年的行动纲领。制造业是国民经济的主体,是立国之本、兴国之器、强国之基。发展制造业的基本方针为质量为先,坚持把质量作为建设制造强国的生命线。某制造企业根据长期检测结果,发现生产的产品质量与生产标准的质量差都服从正态分布,并把质量差在内的产品为优等品,质量差在内的产品为一等品,其余范围内的产品作为废品处理.优等品与一等品统称为正品.现分别从该企业生产的正品中随机抽取1000件,测得产品质量差的样本数据统计如下:
(1)根据频率分布直方图,求样本平均数
(2)根据大量的产品检测数据,检查样本数据的方差的近似值为100,用样本平均数作为的近似值,用样本标准差作为的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表)
[参考数据:若随机变量服从正态分布,则:,,
假如企业包装时要求把3件优等品球和5件一等品装在同一个箱子中,质检员每次从箱子中摸出三件产品进行检验,记摸出三件产品中优等品球的件数为X,求X的分布列以及期望值.
本小题满分12分)
【解析】(1)
.(3分)
(2)由题意样本方差,故.
所以,
由题意,该厂生产的产品为正品的概率
.(6分)
(3)X所有可能为0,1,2,3.
.(10分)
X的分布列为
X 0 1 2 3
P
.(12分)
22.【本题满分12分,】
已知函数,为的导函数.
(Ⅰ)当时,
(i)求曲线在点处的切线方程;
(ii)求函数的单调区间和极值;
(Ⅱ)当时,
求证:对任意,,且,有
22.【详解】(Ⅰ)(i)当时,,.可得,,
所以曲线在点处的切线方程为,即.
(ii)依题意,,.
从而可得,整理可得:,
令,解得.
当变化时,,的变化情况如下表:
0
单调递减 极小值 单调递增
所以,函数的单调递减区间为,单调递增区间为;
的极小值为,无极大值.
(Ⅱ)证明:由,得.
对任意的,,且,令,则
.①
令,.
当时,,
由此可得在单调递增,所以当时,,即
因为,,,
所以
.②
由(Ⅰ)(ii)可知,当时,,即,
故③
由①②③可得.
所以,当时,任意的,,且,有.
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( C )
A. B. C. D.
2.2.已知复数在复平面内对应的点在直线上,则实数(C )
A.-2 B.-1 C.1 D.2
3.若函数是定义在上的奇函数,,当时,,则实数(C)
A. B. 0 C. 1 D. 2
4、设,则“”是“”的 B
A.充分而不必要条 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
5、若点坐标为(,),则点在(? ?B)
A.第一象限?????B.第二象限?????C.第三象限?????D.第四象限
6.函数的图象大致为( c )
A. B.
C. D.
7.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) 2 3 4 5 6
销售额y(万元) 19 25 34 38 44
根据上表可得回归直线方程为,下列说法正确的是( D )
A.回归直线必经过样本点、
B.这组数据的样本中心点未必在回归直线上
C.回归系数6.3的含义是广告费用每增加1万元,销售额实际增加6.3万元
D.据此模型预报广告费用为7万元时销售额为50.9万元
8.已知函数f(x)=-x2+,g(x)=x2ex,若对任意的x2∈[-1,1],存在唯一的x1∈,使得f(x1)=g(x2),则实数a的取值范围是(B)
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.
9.若,,且,则下列不等式恒成立的是( )CD.
A. B. C. D.
10.下列判断正确的是( )BCD
A.已知直线平面,直线平面,则“”是“”的必要不充分条件;
B.若随机变量服从正态分布,,则;
C.若随机变量服从二项分布:,则;
D.是的充分不必要条件.
11.如图是2018年10月—2019年10月中国钢铁同比增速及日均产量统计图,则下列陈述中正确的是( )ABD
A.2019年6月同比增速最大;
B.2019年3月—5月同比增速平稳;
C.2019年8月钢材总产量比2019年9月钢材总产量低;
D.2019年10月钢材总产量约10264万吨。
12.设函数,,给定下列命题,其中是正确命题的是( )ACD
A.不等式的解集为;
B.函数在单调递增,在单调递减;
C.若,则当时,有;
D.若函数有两个极值点,则实数
三、填空题:本题共4小题,每小题5分,共20分.
13.函数在点处的切线与直线垂直,则 .
14.如果的展开式中各项系数之和为4096,则展开式中x的系数为____1215____.
15.函数(,且)的图象恒过定点,且点在角的终边上,则=
16.一圆柱形封闭容器内有一个棱长为2的正四面体,若该正四面体可以绕其中心在容器内任意转动(正四面体顶点恰好触碰到容器内壁可视为可以转动),则容器体积的最小值为
答案
一、选择题答案:
C;2、C;3、C;4、B;5、B;6、C;7、D;8、B
CD;10、BCD;11、ABD;12、ACD
填空题答案:
13、;14、1215;15、;16、
解答题答案:
17、【本题满分10分】
在①AB=A,②AB≠,③BA这三个条件中任选一个,补充在下面问题中,若问题中的实数a存在,求a的取值范围;若不存在,说明理由.
问题:已知集合A=,B=,是否存在实数a,使得 ?
注:如果选择多个条件分别解答,按第一个解答计分.
18.【本题满分12分,】
设函数
(1)若函数y=f(x)的图象关于原点对称,求函数的零点;
(2)若函数在的最大值为-2,求实数a的值.
19、【本题满分12分,】
销售甲种商品所得利润是P万元,它与投入资金t万元的关系有经验公式P=,销售乙种商品所得利润是Q万元,它与投入资金t万元的关系有经验公式Q=bt,其中a,b为常数.现将3万元资金全部投入甲、乙两种商品的销售:若全部投入甲种商品,所得利润为万元;若全部投入乙种商品,所得利润为1万元.若将3万元资金中的x万元投入甲种商品的销售,余下的投入乙种商品的销售,则所得利润总和为f (x)万元.
(1)求函数f (x) 的解析式;
(2)怎样将3万元资金分配给甲、乙两种商品,才能使所得利润总和最大,并求最大值.
2、解:(1)由题意,P=,Q=bt,
故当t=3时,P==,Q=3b=1. …………………… 3分
解得 a=3,b=. …………………… 5分
所以 P=,Q=t.
从而 f(x)=+,x∈[0,3]. ……………………6分
(2)由(1)可得:f(x)=+=-(+).
…………………… 8分
因为x∈[0,3],所以x+1∈[1,4],
故 +≥2,
从而 f(x)≤-2=. …………………… 10分
当且仅当=,即x=2时取等号.
所以f(x)的最大值为 .
答:分别投入2万元、1万元销售甲、乙两种商品时,所得利润总和最大,最大利润是万元. …………………… 12分
20.【本题满分12分,】
如图,在四棱锥中,底面,,,,,是的中点.
(1)求证:平面;
(2)求二面角的余弦值.
20.解:(1)如图,取的中点,连接,.
∵,分别为,的中点,∴,
又且,∴,∴四边形为平行四边形,
∴,又平面,平面,∴平面.
(2)由题意知:,,两两垂直,以为坐标原点,,,所在的直线分别为轴、轴、轴建立如图所示的空间直角坐标系:
∵,分别为,的中点,∴,
又且,∴,∴四边形为平行四边形,
∴,又平面,平面,∴平面.
(2)由题意知:,,两两垂直,以为坐标原点,,,所在的直线分别为轴、轴、轴建立如图所示的空间直角坐标系:
则,,,,,
∴,,,
设平面的法向量,
则,令,则,,∴.
∵平面,∴为平面的一个法向量,
∴,
∵二面角为锐二面角,∴二面角的余弦值为.
21.(12分)《中国制造2025》是经国务院总理李克强签批,由国务院于2015年5月印发的部署全面推进实施制造强国的战略文件,是中国实施制造强国战略第一个十年的行动纲领。制造业是国民经济的主体,是立国之本、兴国之器、强国之基。发展制造业的基本方针为质量为先,坚持把质量作为建设制造强国的生命线。某制造企业根据长期检测结果,发现生产的产品质量与生产标准的质量差都服从正态分布,并把质量差在内的产品为优等品,质量差在内的产品为一等品,其余范围内的产品作为废品处理.优等品与一等品统称为正品.现分别从该企业生产的正品中随机抽取1000件,测得产品质量差的样本数据统计如下:
(1)根据频率分布直方图,求样本平均数
(2)根据大量的产品检测数据,检查样本数据的方差的近似值为100,用样本平均数作为的近似值,用样本标准差作为的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表)
[参考数据:若随机变量服从正态分布,则:,,
假如企业包装时要求把3件优等品球和5件一等品装在同一个箱子中,质检员每次从箱子中摸出三件产品进行检验,记摸出三件产品中优等品球的件数为X,求X的分布列以及期望值.
本小题满分12分)
【解析】(1)
.(3分)
(2)由题意样本方差,故.
所以,
由题意,该厂生产的产品为正品的概率
.(6分)
(3)X所有可能为0,1,2,3.
.(10分)
X的分布列为
X 0 1 2 3
P
.(12分)
22.【本题满分12分,】
已知函数,为的导函数.
(Ⅰ)当时,
(i)求曲线在点处的切线方程;
(ii)求函数的单调区间和极值;
(Ⅱ)当时,
求证:对任意,,且,有
22.【详解】(Ⅰ)(i)当时,,.可得,,
所以曲线在点处的切线方程为,即.
(ii)依题意,,.
从而可得,整理可得:,
令,解得.
当变化时,,的变化情况如下表:
0
单调递减 极小值 单调递增
所以,函数的单调递减区间为,单调递增区间为;
的极小值为,无极大值.
(Ⅱ)证明:由,得.
对任意的,,且,令,则
.①
令,.
当时,,
由此可得在单调递增,所以当时,,即
因为,,,
所以
.②
由(Ⅰ)(ii)可知,当时,,即,
故③
由①②③可得.
所以,当时,任意的,,且,有.
同课章节目录
