高中物理人教版选修3-5 作业题 17-2 光的粒子性 Word版含解析
文档属性
| 名称 | 高中物理人教版选修3-5 作业题 17-2 光的粒子性 Word版含解析 |

|
|
| 格式 | DOC | ||
| 文件大小 | 125.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-16 13:57:00 | ||
图片预览


文档简介
光的粒子性
时间:45分钟
一、选择题(1~6为单选,7~9为多选)
1.光电效应中,从同一金属逸出的电子的动能的最大值( A )
A.只跟入射光的频率有关
B.只跟入射光的强度有关
C.跟入射光的频率和强度都有关
D.除跟入射光的频率和强度有关外,还和光照时间有关
解析:根据光电效应的规律知,光电子的最大初动能Ek只取决于入射光的频率ν,故A正确.
2.关于光电效应的规律,下列说法中正确的是( D )
A.只有入射光的波长大于该金属的极限波长,光电效应才能发生
B.光电子的最大初动能跟入射光的强度成正比
C.发生光电效应的时间一般都大于10-7 s
D.发生光电效应时,单位时间内从金属内逸出的光电子数与入射光的强度成正比
解析:由ε=hν=h知,当入射光波长大于极限波长时,不能发生光电效应,故A错.由Ek=hν-W0知,最大初动能由入射光频率决定,与入射光的强度无关,故B错.发生光电效应的时间一般不超过10-9 s,故C错.
3.对于任何一种金属,能发生光电效应的条件是( D )
A.入射光的强度大于某一极限强度
B.入射光的波长大于某一极限波长
C.入射光照射时间大于某一极限时间
D.入射光的频率不低于某一极限频率
4.关于光电效应现象,下列说法正确的是( D )
A.只有入射光的波长大于使该金属发生光电效应的极限波长,才能发生光电效应现象
B.在光电效应现象中,产生的光电子的最大初动能跟入射光的频率成正比
C.产生的光电子最大初动能与入射光的强度成正比
D.在入射光频率一定时,单位时间内从金属中逸出的光电子个数与入射光的强度成正比
解析:当入射光频率不低于极限频率时才能发生光电效应,设此时波长为λ0,极限频率为νc,则光速c=λ0νc,可知当入射光的波长大于极限波长λ0时,其频率将小于极限频率νc,所以大于极限波长的光不能使金属发生光电效应,因此选项A错误.由光电效应方程Ek=hν-W0可知,光电子的最大初动能随入射光频率的增大而增大,但并不与入射光频率成正比,因此选项B错误.由于光电子的最大初动能与入射光的强度无关,显然选项C错误.若入射光强度增大到原来的n倍,则单位时间内入射光的能量就增大到原来的n倍.在入射光频率一定时,单个光子的能量不变,则单位时间内入射的光子数将增大到原来的n倍,因此选项D正确.
5.2017年年初,我国研制的“大连光源”——极紫外自由电子激光装置,发出了波长在100 nm(1 nm=10-9 m)附近连续可调的世界上最强的极紫外激光脉冲.大连光源因其光子的能量大、密度高,可在能源利用、光刻技术、雾霾治理等领域的研究中发挥重要作用.一个处于极紫外波段的光子所具有的能量可以电离一个分子,但又不会把分子打碎.据此判断,能够电离一个分子的能量约为(取普朗克常量h=6.6×10-34 J·s,真空光速c=3×108 m/s)( B )
A.10-21 J B.10-18 J
C.10-15 J D.10-12 J
解析:本题考查光子能量.由题意知,电离一个分子的能量等于照射分子的光子能量,E=hν=h=2×10-18 J,故选项B正确.
6.下表是按照密立根的方法进行光电效应实验时得到的某金属的遏止电压Uc和入射光的频率ν的几组数据:
Uc/V 0.541 0.637 0.714 0.809 0.878
ν/1014 Hz 5.644 5.888 6.098 6.303 6.501
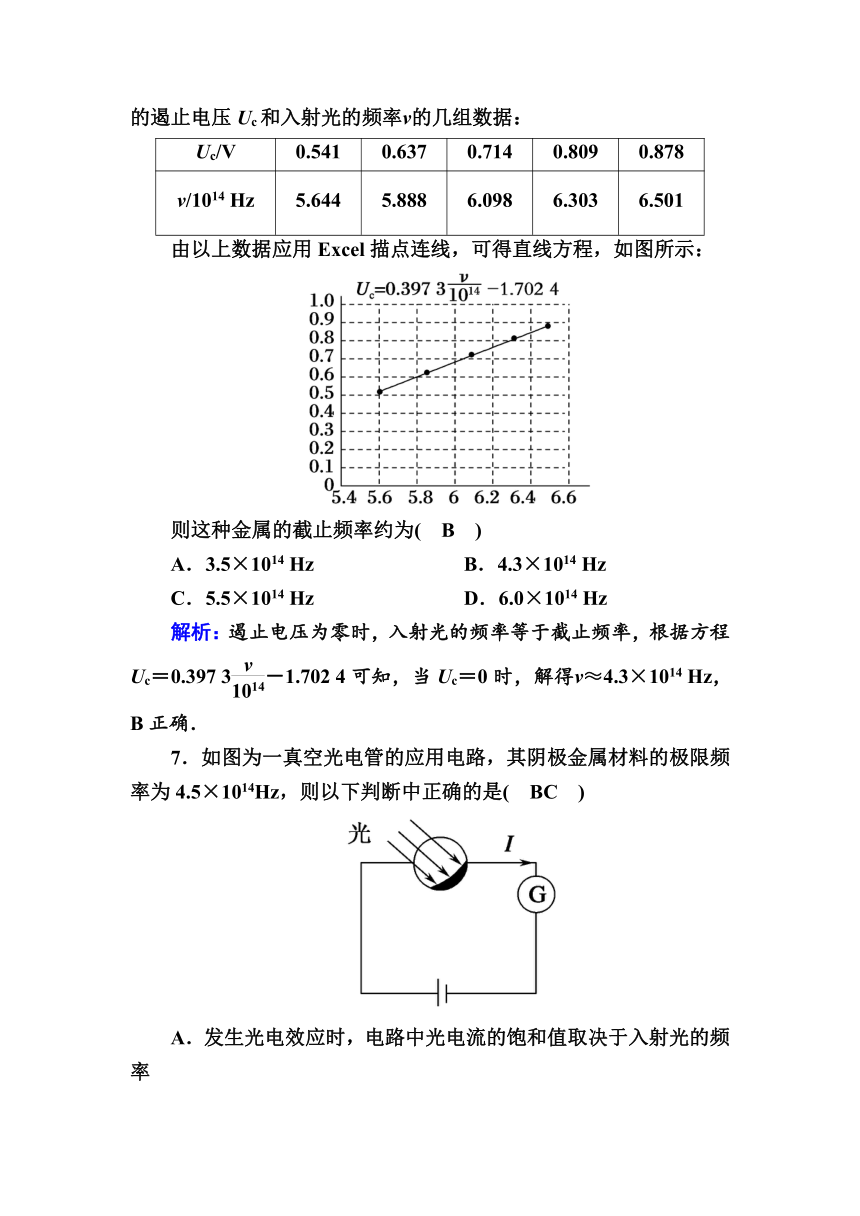
由以上数据应用Excel描点连线,可得直线方程,如图所示:
则这种金属的截止频率约为( B )
A.3.5×1014 Hz B.4.3×1014 Hz
C.5.5×1014 Hz D.6.0×1014 Hz
解析:遏止电压为零时,入射光的频率等于截止频率,根据方程Uc=0.397 3-1.702 4可知,当Uc=0时,解得ν≈4.3×1014 Hz,B正确.
7.如图为一真空光电管的应用电路,其阴极金属材料的极限频率为4.5×1014Hz,则以下判断中正确的是( BC )
A.发生光电效应时,电路中光电流的饱和值取决于入射光的频率
B.发生光电效应时,电路中光电流的饱和值取决于入射光的强度
C.用λ=0.5 μm的光照射光电管时,电路中有光电流产生
D.光照射时间越长,电路中的电流越大
解析:在光电管中若发生了光电效应,单位时间内发射光电子的数目只与入射光的强度有关,光电流的饱和值只与单位时间内发射光电子的数目有关.据此可判断A、D错误.波长λ=0.5 μm的光子的频率ν== Hz=6×1014 Hz>4.5×1014 Hz,可发生光电效应,所以B、C正确.
8.在光电效应实验中,两个实验小组分别在各自的实验室,约定用相同频率的单色光分别照射锌和银的表面,结果都能发生光电效应,如图甲所示,并记录相关数据如图乙所示.对于这两组实验,下列判断正确的是( BCD )
A.饱和光电流一定不同
B.因为材料不同逸出功不同,所以遏止电压Uc不同
C.光电子的最大初动能不同
D.因为光强不确定,所以单位时间内逸出的光电子数可能相同
解析:虽然光的频率相同,但光强不确定,因此单位时间内逸出的光电子数可能相同,而饱和光电流不一定相同,故A错误,D正确;根据光电效应方程Ek=hν-W0和eUc=Ek可知,在频率相同、逸出功不同的情况下,遏止电压不相同,光电子的最大初动能也不同,故B,C正确.
9.已知能使某金属产生光电效应的极限频率为νc,则( AB )
A.当用频率为2νc的单色光照射该金属时,一定能产生光电子
B.当用频率为2νc的单色光照射该金属时,所产生的光电子的最大初动能为hνc
C.当入射光的频率ν大于νc时,若ν增大,则逸出功增大
D.当入射光的频率ν大于νc时,若ν增大一倍,则光电子的最大初动能也增大一倍
解析:因入射光的频率大于极限频率时会产生光电效应,所以A正确;因为金属的极限频率为νc,所以逸出功W0=hνc,再由Ek=hν-W0得,Ek=2hνc-hνc=hνc,B正确;因为逸出功是光电子恰好逸出时需要做的功,对于同种金属是恒定的,故C错误;由Ek=hν-W0=hν-hνc=h(ν-νc)可得,当ν增大一倍时:=≠2,故D错误.
二、非选择题
10.用波长为λ的光照射金属的表面,当遏止电压取某个值时,光电流被截止.当光的波长改变为原波长的后,已查明使电流截止的遏止电压必须增大到原值的η倍.已知该金属的逸出功为W0,试计算原入射光的波长λ.
答案:
解析:利用eUc=hν-W0,按题意可写出两个方程:
eUc=h-W0,
以及eηUc=h-W0,
两式相减得(η-1)eUc=h(n-1).
再将上述第一式代入,便有
(η-1)=h(n-1),
λ=,式中W0是金属的逸出功.
11.用功率P0=1 W的点光源照射离光源r=3 m处的一块金属薄片,已知光源发出的是波长为λ=589 nm的单色光,试计算:
(1)1 s内打到金属薄片1 cm2面积上的光子数.
(2)若取该金属薄片原子半径r1=0.5×10-10 m,则金属薄片表面上每个原子平均需隔多长时间才能接收到一个光子?
答案:(1)2.61×1012个 (2)4 878.0 s
解析:(1)离光源r=3 m处的金属板每1 s内单位面积上接收的光的能量为E== J≈8.8×10-3 J=5.5×1016 eV,所以1 s内传到金属板1 cm2面积上的光能E0=ES=5.5×1012 eV.又因为这种单色光一个光子的能量E0′=hν== J≈3.375×10-19 J,即E0′≈2.11 eV,所以1 s内打到金属板1 cm2面积上的光子数n==≈2.61×1012个.
(2)金属板可以看成由金属原子密集排列组成的,每个金属原子的最大截面积为S1=πr=3.14×(0.5×10-10)2 m2=7.85×10-21 m2,则每个原子每秒内接收到的光子数为n1=nS1×104=2.61×1012×7.85×10-21×104个≈2.05×10-4个,每两个光子落在同一个原子上的时间间隔Δt== s≈4 878.0 s,说明光电效应中光子与原子之间的作用是一对一的.
12.在绿色植物光合作用下,每放出1 mol的O2,植物储存451.5 kJ能量,绿色植物能量转化效率(即植物储存的能量与植物吸收光的能量之比)约为50%,求绿色植物每放出1个氧分子要吸收多少个波长为6.63×10-7 m的光.(普朗克常量h=6.63×10-34 J·s,阿伏加德罗常量NA=6.02×1023 mol-1)
答案:5个
解析:每放出1个氧分子储存能量为 J,
每放出1个氧分子要吸收能量为
E= J=1.5×10-18 J,
一个光子的能量为:E1==3×10-19 J,
光子个数为:n==5个.
时间:45分钟
一、选择题(1~6为单选,7~9为多选)
1.光电效应中,从同一金属逸出的电子的动能的最大值( A )
A.只跟入射光的频率有关
B.只跟入射光的强度有关
C.跟入射光的频率和强度都有关
D.除跟入射光的频率和强度有关外,还和光照时间有关
解析:根据光电效应的规律知,光电子的最大初动能Ek只取决于入射光的频率ν,故A正确.
2.关于光电效应的规律,下列说法中正确的是( D )
A.只有入射光的波长大于该金属的极限波长,光电效应才能发生
B.光电子的最大初动能跟入射光的强度成正比
C.发生光电效应的时间一般都大于10-7 s
D.发生光电效应时,单位时间内从金属内逸出的光电子数与入射光的强度成正比
解析:由ε=hν=h知,当入射光波长大于极限波长时,不能发生光电效应,故A错.由Ek=hν-W0知,最大初动能由入射光频率决定,与入射光的强度无关,故B错.发生光电效应的时间一般不超过10-9 s,故C错.
3.对于任何一种金属,能发生光电效应的条件是( D )
A.入射光的强度大于某一极限强度
B.入射光的波长大于某一极限波长
C.入射光照射时间大于某一极限时间
D.入射光的频率不低于某一极限频率
4.关于光电效应现象,下列说法正确的是( D )
A.只有入射光的波长大于使该金属发生光电效应的极限波长,才能发生光电效应现象
B.在光电效应现象中,产生的光电子的最大初动能跟入射光的频率成正比
C.产生的光电子最大初动能与入射光的强度成正比
D.在入射光频率一定时,单位时间内从金属中逸出的光电子个数与入射光的强度成正比
解析:当入射光频率不低于极限频率时才能发生光电效应,设此时波长为λ0,极限频率为νc,则光速c=λ0νc,可知当入射光的波长大于极限波长λ0时,其频率将小于极限频率νc,所以大于极限波长的光不能使金属发生光电效应,因此选项A错误.由光电效应方程Ek=hν-W0可知,光电子的最大初动能随入射光频率的增大而增大,但并不与入射光频率成正比,因此选项B错误.由于光电子的最大初动能与入射光的强度无关,显然选项C错误.若入射光强度增大到原来的n倍,则单位时间内入射光的能量就增大到原来的n倍.在入射光频率一定时,单个光子的能量不变,则单位时间内入射的光子数将增大到原来的n倍,因此选项D正确.
5.2017年年初,我国研制的“大连光源”——极紫外自由电子激光装置,发出了波长在100 nm(1 nm=10-9 m)附近连续可调的世界上最强的极紫外激光脉冲.大连光源因其光子的能量大、密度高,可在能源利用、光刻技术、雾霾治理等领域的研究中发挥重要作用.一个处于极紫外波段的光子所具有的能量可以电离一个分子,但又不会把分子打碎.据此判断,能够电离一个分子的能量约为(取普朗克常量h=6.6×10-34 J·s,真空光速c=3×108 m/s)( B )
A.10-21 J B.10-18 J
C.10-15 J D.10-12 J
解析:本题考查光子能量.由题意知,电离一个分子的能量等于照射分子的光子能量,E=hν=h=2×10-18 J,故选项B正确.
6.下表是按照密立根的方法进行光电效应实验时得到的某金属的遏止电压Uc和入射光的频率ν的几组数据:
Uc/V 0.541 0.637 0.714 0.809 0.878
ν/1014 Hz 5.644 5.888 6.098 6.303 6.501
由以上数据应用Excel描点连线,可得直线方程,如图所示:
则这种金属的截止频率约为( B )
A.3.5×1014 Hz B.4.3×1014 Hz
C.5.5×1014 Hz D.6.0×1014 Hz
解析:遏止电压为零时,入射光的频率等于截止频率,根据方程Uc=0.397 3-1.702 4可知,当Uc=0时,解得ν≈4.3×1014 Hz,B正确.
7.如图为一真空光电管的应用电路,其阴极金属材料的极限频率为4.5×1014Hz,则以下判断中正确的是( BC )
A.发生光电效应时,电路中光电流的饱和值取决于入射光的频率
B.发生光电效应时,电路中光电流的饱和值取决于入射光的强度
C.用λ=0.5 μm的光照射光电管时,电路中有光电流产生
D.光照射时间越长,电路中的电流越大
解析:在光电管中若发生了光电效应,单位时间内发射光电子的数目只与入射光的强度有关,光电流的饱和值只与单位时间内发射光电子的数目有关.据此可判断A、D错误.波长λ=0.5 μm的光子的频率ν== Hz=6×1014 Hz>4.5×1014 Hz,可发生光电效应,所以B、C正确.
8.在光电效应实验中,两个实验小组分别在各自的实验室,约定用相同频率的单色光分别照射锌和银的表面,结果都能发生光电效应,如图甲所示,并记录相关数据如图乙所示.对于这两组实验,下列判断正确的是( BCD )
A.饱和光电流一定不同
B.因为材料不同逸出功不同,所以遏止电压Uc不同
C.光电子的最大初动能不同
D.因为光强不确定,所以单位时间内逸出的光电子数可能相同
解析:虽然光的频率相同,但光强不确定,因此单位时间内逸出的光电子数可能相同,而饱和光电流不一定相同,故A错误,D正确;根据光电效应方程Ek=hν-W0和eUc=Ek可知,在频率相同、逸出功不同的情况下,遏止电压不相同,光电子的最大初动能也不同,故B,C正确.
9.已知能使某金属产生光电效应的极限频率为νc,则( AB )
A.当用频率为2νc的单色光照射该金属时,一定能产生光电子
B.当用频率为2νc的单色光照射该金属时,所产生的光电子的最大初动能为hνc
C.当入射光的频率ν大于νc时,若ν增大,则逸出功增大
D.当入射光的频率ν大于νc时,若ν增大一倍,则光电子的最大初动能也增大一倍
解析:因入射光的频率大于极限频率时会产生光电效应,所以A正确;因为金属的极限频率为νc,所以逸出功W0=hνc,再由Ek=hν-W0得,Ek=2hνc-hνc=hνc,B正确;因为逸出功是光电子恰好逸出时需要做的功,对于同种金属是恒定的,故C错误;由Ek=hν-W0=hν-hνc=h(ν-νc)可得,当ν增大一倍时:=≠2,故D错误.
二、非选择题
10.用波长为λ的光照射金属的表面,当遏止电压取某个值时,光电流被截止.当光的波长改变为原波长的后,已查明使电流截止的遏止电压必须增大到原值的η倍.已知该金属的逸出功为W0,试计算原入射光的波长λ.
答案:
解析:利用eUc=hν-W0,按题意可写出两个方程:
eUc=h-W0,
以及eηUc=h-W0,
两式相减得(η-1)eUc=h(n-1).
再将上述第一式代入,便有
(η-1)=h(n-1),
λ=,式中W0是金属的逸出功.
11.用功率P0=1 W的点光源照射离光源r=3 m处的一块金属薄片,已知光源发出的是波长为λ=589 nm的单色光,试计算:
(1)1 s内打到金属薄片1 cm2面积上的光子数.
(2)若取该金属薄片原子半径r1=0.5×10-10 m,则金属薄片表面上每个原子平均需隔多长时间才能接收到一个光子?
答案:(1)2.61×1012个 (2)4 878.0 s
解析:(1)离光源r=3 m处的金属板每1 s内单位面积上接收的光的能量为E== J≈8.8×10-3 J=5.5×1016 eV,所以1 s内传到金属板1 cm2面积上的光能E0=ES=5.5×1012 eV.又因为这种单色光一个光子的能量E0′=hν== J≈3.375×10-19 J,即E0′≈2.11 eV,所以1 s内打到金属板1 cm2面积上的光子数n==≈2.61×1012个.
(2)金属板可以看成由金属原子密集排列组成的,每个金属原子的最大截面积为S1=πr=3.14×(0.5×10-10)2 m2=7.85×10-21 m2,则每个原子每秒内接收到的光子数为n1=nS1×104=2.61×1012×7.85×10-21×104个≈2.05×10-4个,每两个光子落在同一个原子上的时间间隔Δt== s≈4 878.0 s,说明光电效应中光子与原子之间的作用是一对一的.
12.在绿色植物光合作用下,每放出1 mol的O2,植物储存451.5 kJ能量,绿色植物能量转化效率(即植物储存的能量与植物吸收光的能量之比)约为50%,求绿色植物每放出1个氧分子要吸收多少个波长为6.63×10-7 m的光.(普朗克常量h=6.63×10-34 J·s,阿伏加德罗常量NA=6.02×1023 mol-1)
答案:5个
解析:每放出1个氧分子储存能量为 J,
每放出1个氧分子要吸收能量为
E= J=1.5×10-18 J,
一个光子的能量为:E1==3×10-19 J,
光子个数为:n==5个.
