鲁教版(五四制)七年级数学上册2.3简单的轴对称图形课件 (共23张PPT)
文档属性
| 名称 | 鲁教版(五四制)七年级数学上册2.3简单的轴对称图形课件 (共23张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 903.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 00:00:00 | ||
图片预览









文档简介
(共23张PPT)
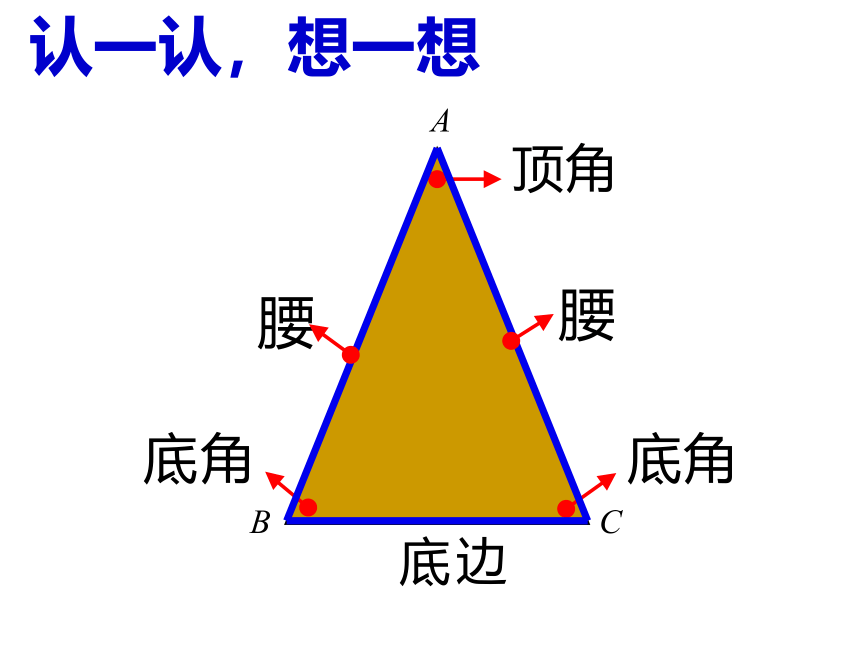
认一认,想一想
等腰三角形
A
B
C
学习目标
1.能准确说出等腰三角形的对称性,作出等腰三角形的对称轴。
2.掌握等腰三角形的性质,并利用前面所学的知识证明等腰三角形的性质。
3.应用等腰三角形的性质进行计算和证明。
自主学习
如图,拿出一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它打开,得到的△ABC
有
什么特点?
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
将等腰三角形对折,使两腰AB,AC重叠在一起,折痕为AD.你能找出其中重合的线段和角吗?
A
B
C
自主学习
1、等腰三角形是轴对称图形吗?如果是,请找出它的对称轴。
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD=∠CAD
∠ADB=∠ADC
①等腰三角形是轴对称图形。
A
B
C
课内探究
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD=∠CAD
∠ADB=∠ADC
2、等腰三角形顶角平分线所在的直线是它的对称轴吗?
∠BAD=∠CAD
等腰三角形顶角平分线所在的直线是它的对称轴.
A
B
C
课内探究
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD=∠CAD
∠ADB=∠ADC
3、等腰三角形底边上的中线所在的直线是它的对称轴吗?底边上的高所在的直线呢?
BD=CD
等腰三角形底边上的中线所在的直线是它的对称轴
∠ADB=∠ADC
等腰三角形底边上的高所在的直线是它的对称轴
A
B
C
等腰三角形的性质2
D
等腰三角形底边上的中线所在的直线是它的对称轴
等腰三角形底边上的高所在的直线是它的对称轴
等腰三角形顶角平分线所在的直线是它的对称轴.
②等腰三角形顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”)它们所在的直线都是等腰三角形的对称轴.
在△ABC中,AB=AC,D在BC上
1.
如果
AD⊥BC,
那么∠BAD=∠___,
BD=___.
2.
如果∠BAD=∠CAD
,
那么AD⊥___,
BD=___.
3.
如果BD=CD,
那么∠BAD=∠___,
AD⊥___.
CAD
CAD
CD
CD
BC
BC
几何语言表示
D
·→
画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?
“三线合一”应该对应等腰三角形顶角的平分线,底边上的中线和底边上的高.
为什么不一样呢?
想一想?
等腰三角形的性质
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
例1
已知:△ABC中,AB=AC.小明想作∠BAC的平分线,但他没有量角器,只有刻度尺,他如何作出∠BAC的平分线?
C
B
A
D
1
2
C
B
A
分析:根据“三线合一”,只需作出三角形底边BC上的中线。
解:
取BC的中点D,
连结AD,
∵
△ABC中,AB=AC,
BD=CD
∴∠1=∠2(三线合一)
即AD是△ABC顶角∠BAC
的平分线。
应用
A
B
C
等腰三角形的性质3
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD=∠CAD
∠ADB=∠ADC
4、沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由。
∠B
=∠C
③等腰三角形的两个底角相等。
(也称“等边对等角”)
注意:
在
三角形中,等边对等角
同一个
在△ABC中,
∵
AC=AB(
)
∴
∠B=∠C
(
)
已知
等边对等角
C
B
A
几何语言表示
如何验证“等边对等角”?
已知:如图,△ABC中,AB=AC。
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
合作探究
D
证明:作△ABC的角平分线AD,
则有∠BAD=∠CAD。
在△ABD和△ACD中
AB=AC(已知)
AD=AD(公共边)
∴△ABD≌△ACD
(SAS)
∴∠B=∠C(全等三角形对应角相等)
.
∠BAD=∠CAD(已作)
还可以作BC边上的中线或高来解决验证。
等腰三角形的性质
3.
等腰三角形的两个底角相等(等边对等角)
例2
在△ABC中,已知AB=AC,且
∠
A=120°
,求∠B,∠C的度数.
解:
∵△ABC中,AB=AC(已知)
∴∠B=∠C(等边对等角)
又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∠A=120°
(已知)
∴∠B+∠C=60o
∠B=30°
∠C=30°
C
B
A
应用
等腰三角形的底角可以是直角或钝角吗?为什么?
想一想?
A
B
C
D
归纳总结
等腰三角形的性质
1、等腰三角形是轴对称图形。
2、等腰三角形顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”)它们所在的直线都是等腰三角形的对称轴.
3、等腰三角形的两个底角
相等(也称“等边对等角”)。
巩固练习
1、填空
(1)已知等腰三角形的顶角是70o,则它的其它两角的度数是
。
(2)已知等腰三角形的底角是70o,则它的其它两角的度数是
。
(3)已知等腰三角形的一个内角是70o,则它的其它两角的度数是
。
(4)等腰直角三角形的每一个锐角都等于___.
55o、55o
70o、40o
55o、55o或70o、40o
45°
2.判断下列语句是否正确.
(1)等腰三角形的角平分线、中线和高互相重合.(
)
(2)有一个角是60°的等腰三角形,其他两个内角也为60°.
(
)
(3)等腰三角形的底角一定是锐角.
(
)
(4)钝角三角形不可能是等腰三角形
.
(
)
×
×
3.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求
∠1和∠ADC的度数.
∵
AB=AC,D是BC边上的中点,
,∠ADC=
90°
∵
∠BAC=180°-30°-30°=120°,
(三线合一).
解析:
∠C=
∠B=30°(等边对等角)
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称等边对等角).
∵AB=AC,
∴∠B=∠C.
等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一).
∵AB=AC,∠1=∠2,
∴AD⊥BC,BD=CD.
课堂总结
这节课你学习了那些内容?
⑵“三线合一”是对等腰三角形的顶角平分线、底边上的中线和底边上的高而言的.
⑴“等边对等角”必须在同一个等腰三角形中才成立.
要注意!
课后作业
综合训练P50-51
认一认,想一想
等腰三角形
A
B
C
学习目标
1.能准确说出等腰三角形的对称性,作出等腰三角形的对称轴。
2.掌握等腰三角形的性质,并利用前面所学的知识证明等腰三角形的性质。
3.应用等腰三角形的性质进行计算和证明。
自主学习
如图,拿出一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它打开,得到的△ABC
有
什么特点?
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
将等腰三角形对折,使两腰AB,AC重叠在一起,折痕为AD.你能找出其中重合的线段和角吗?
A
B
C
自主学习
1、等腰三角形是轴对称图形吗?如果是,请找出它的对称轴。
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD=∠CAD
∠ADB=∠ADC
①等腰三角形是轴对称图形。
A
B
C
课内探究
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD=∠CAD
∠ADB=∠ADC
2、等腰三角形顶角平分线所在的直线是它的对称轴吗?
∠BAD=∠CAD
等腰三角形顶角平分线所在的直线是它的对称轴.
A
B
C
课内探究
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD=∠CAD
∠ADB=∠ADC
3、等腰三角形底边上的中线所在的直线是它的对称轴吗?底边上的高所在的直线呢?
BD=CD
等腰三角形底边上的中线所在的直线是它的对称轴
∠ADB=∠ADC
等腰三角形底边上的高所在的直线是它的对称轴
A
B
C
等腰三角形的性质2
D
等腰三角形底边上的中线所在的直线是它的对称轴
等腰三角形底边上的高所在的直线是它的对称轴
等腰三角形顶角平分线所在的直线是它的对称轴.
②等腰三角形顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”)它们所在的直线都是等腰三角形的对称轴.
在△ABC中,AB=AC,D在BC上
1.
如果
AD⊥BC,
那么∠BAD=∠___,
BD=___.
2.
如果∠BAD=∠CAD
,
那么AD⊥___,
BD=___.
3.
如果BD=CD,
那么∠BAD=∠___,
AD⊥___.
CAD
CAD
CD
CD
BC
BC
几何语言表示
D
·→
画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?
“三线合一”应该对应等腰三角形顶角的平分线,底边上的中线和底边上的高.
为什么不一样呢?
想一想?
等腰三角形的性质
2.等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
例1
已知:△ABC中,AB=AC.小明想作∠BAC的平分线,但他没有量角器,只有刻度尺,他如何作出∠BAC的平分线?
C
B
A
D
1
2
C
B
A
分析:根据“三线合一”,只需作出三角形底边BC上的中线。
解:
取BC的中点D,
连结AD,
∵
△ABC中,AB=AC,
BD=CD
∴∠1=∠2(三线合一)
即AD是△ABC顶角∠BAC
的平分线。
应用
A
B
C
等腰三角形的性质3
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD=∠CAD
∠ADB=∠ADC
4、沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由。
∠B
=∠C
③等腰三角形的两个底角相等。
(也称“等边对等角”)
注意:
在
三角形中,等边对等角
同一个
在△ABC中,
∵
AC=AB(
)
∴
∠B=∠C
(
)
已知
等边对等角
C
B
A
几何语言表示
如何验证“等边对等角”?
已知:如图,△ABC中,AB=AC。
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
合作探究
D
证明:作△ABC的角平分线AD,
则有∠BAD=∠CAD。
在△ABD和△ACD中
AB=AC(已知)
AD=AD(公共边)
∴△ABD≌△ACD
(SAS)
∴∠B=∠C(全等三角形对应角相等)
.
∠BAD=∠CAD(已作)
还可以作BC边上的中线或高来解决验证。
等腰三角形的性质
3.
等腰三角形的两个底角相等(等边对等角)
例2
在△ABC中,已知AB=AC,且
∠
A=120°
,求∠B,∠C的度数.
解:
∵△ABC中,AB=AC(已知)
∴∠B=∠C(等边对等角)
又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∠A=120°
(已知)
∴∠B+∠C=60o
∠B=30°
∠C=30°
C
B
A
应用
等腰三角形的底角可以是直角或钝角吗?为什么?
想一想?
A
B
C
D
归纳总结
等腰三角形的性质
1、等腰三角形是轴对称图形。
2、等腰三角形顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”)它们所在的直线都是等腰三角形的对称轴.
3、等腰三角形的两个底角
相等(也称“等边对等角”)。
巩固练习
1、填空
(1)已知等腰三角形的顶角是70o,则它的其它两角的度数是
。
(2)已知等腰三角形的底角是70o,则它的其它两角的度数是
。
(3)已知等腰三角形的一个内角是70o,则它的其它两角的度数是
。
(4)等腰直角三角形的每一个锐角都等于___.
55o、55o
70o、40o
55o、55o或70o、40o
45°
2.判断下列语句是否正确.
(1)等腰三角形的角平分线、中线和高互相重合.(
)
(2)有一个角是60°的等腰三角形,其他两个内角也为60°.
(
)
(3)等腰三角形的底角一定是锐角.
(
)
(4)钝角三角形不可能是等腰三角形
.
(
)
×
×
3.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求
∠1和∠ADC的度数.
∵
AB=AC,D是BC边上的中点,
,∠ADC=
90°
∵
∠BAC=180°-30°-30°=120°,
(三线合一).
解析:
∠C=
∠B=30°(等边对等角)
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称等边对等角).
∵AB=AC,
∴∠B=∠C.
等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一).
∵AB=AC,∠1=∠2,
∴AD⊥BC,BD=CD.
课堂总结
这节课你学习了那些内容?
⑵“三线合一”是对等腰三角形的顶角平分线、底边上的中线和底边上的高而言的.
⑴“等边对等角”必须在同一个等腰三角形中才成立.
要注意!
课后作业
综合训练P50-51
