高中数学人教A版必修1第二章指数函数及其性质教学设计案例(Word)
文档属性
| 名称 | 高中数学人教A版必修1第二章指数函数及其性质教学设计案例(Word) |

|
|
| 格式 | docx | ||
| 文件大小 | 717.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 21:55:49 | ||
图片预览



文档简介
教学设计案例
《§2.1.2
指数函数及其性质》教学设计
课
题
§2.1.2
指数函数及其性质
(第一课时)
教材版本
人民教育出版社普通高中课程标准实验教科书数学必修1
A版
教学目标
1.
通过实例引入指数函数,激发学生的学习兴趣,体会指数函数是一类重要的函数模型,体会数学的应用价值;
2.
通过牛肉面的实例,激发学生对家乡的热爱之情;
3.
通过探究指数函数的底数a的条件,明确数学概念的严谨性和科学性,并领会分类讨论的思想方法;
4.
掌握指数函数的概念,并能根据定义判断一个函数是否为指数函数;
5.
通过现代信息技术的合理利用,让学生体会到现代信息技术是认识世界的有效手段;
6.
通过观察指数函数的图象,分析、归纳、总结、自主建构指数函数的性质;
7.
体会数形结合的思想,培养学生发现、分析、解决问题的能力;
8.
在探究过程中,让学生体会从特殊到一般的数学方法;
9.
会用指数函数及其性质解决指数函数相关问题.
教学重点
指数函数的概念和性质.
教学难点
用数形结合的方法从具体到一般地探索、概括指数函数的性质.
授课类型
新授课
课时安排
第一课时(40分钟)
教学方法
引导启发式、参与发现式
教学用具
多媒体课件、坐标纸、性质列表.
教学过程
活动一
体会身边的指数模型
1.教师请学生展示牛肉面的拉面过程,让学生抽象出拉面师两手之间的面的根数与对折次数之间的关系.
(设计牛肉面的情境,旨在激起学生学习数学的热情,调动学生主体参与学习活动的积极性,并让学生体会身边的指数模型,同时感受家乡美.)
2.庄子在《天下篇》中说:“一尺之棰,日取其半,万世不竭.”请学生写出截取第x次后,木棰的剩留量y与x的关系式.
(设计这个情境,旨在渗透数学史.)
3.回顾两个情境,教师提问情境中涉及到的两个关系式和是不是函数,为指数函数定义的探究做好铺垫.
活动二
探究指数函数的定义
1.将活动一得到的关系式中的定义域扩充到实数集范围,即.提问学生上述关系式是否为函数?
2.如果将中的底数2替换为常数a,它还是函数吗?
学生分小组讨论,教师引导学生对参数a的限定条件进行讨论,得出且的结论.
教师也参与到学生的讨论中,对有困难的小组进行启发.
(采用小组合作这种方式,一方面是考虑到小组合作这种特殊的学习模式具有信息密度大、传递速度快等特点,另一方面是为了培养学生的合作意识和语言表达能力,让学生尝试“说数学”.)
3.讨论结束后,小组派代表向全班同学展示讨论结果.
(学生发表观点,教师及时实施多元评价.)
交流后,教师完善定义并用多媒体展示指数函数定义,并指出指数函数的定义是形式化的定义,我们必须严格依照它的形式来判断一个函数是否为指数函数.并用多媒体展示形式中的三个要求.
一般地,函数y=ax(a>0,且a≠1)叫做指数函数(exponential
function),其中x是自变量,函数的定义域是R.
想一想
下列四个函数是不是指数函数?
教师随机提问.
(这个环节是为了让学生进一步理解指数函数的形式化定义.)
活动三
探究指数函数的图象
学生活动1
分小组在事先准备好的坐标纸上用描点法作出下面几个指数函数的图象.
与;与;与.
要求:每位同学从上述三组函数中选择一组底数互为倒数的指数函数作出函数的图象.
(设置这个环节是为了让学生尝试“做数学”,体会知识的生成过程,教师对有困难的同学进行个别指导.)
学生活动2
选代表展示自己画出的图象.教师给予及时评价.
(教师鼓励性的及时评价有利于学生建立学习数学、探索知识的自信心.)
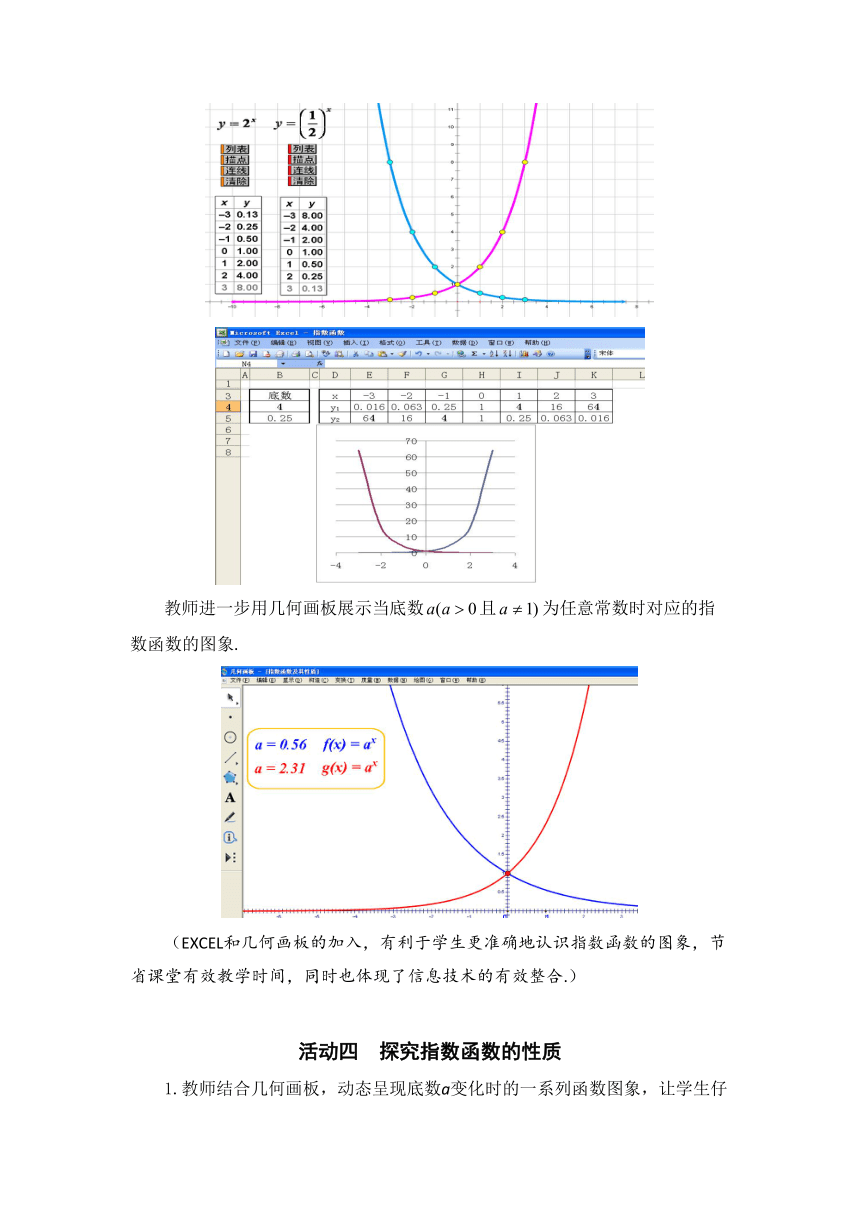
展示交流后,教师用几何画板作出第一组的两个图象,再用EXCEL画出第二组和第三组的4个函数图象.并请学生对比自己画出的图象.
教师进一步用几何画板展示当底数且为任意常数时对应的指数函数的图象.
(EXCEL和几何画板的加入,有利于学生更准确地认识指数函数的图象,节省课堂有效教学时间,同时也体现了信息技术的有效整合.)
活动四
探究指数函数的性质
1.教师结合几何画板,动态呈现底数a变化时的一系列函数图象,让学生仔细观察图象特征,进而归纳相应性质.学生积极发言.
学情预设
(1).定义域是R;
(2).图象恒过(0,1)点;
(3).值域是(0,+∞);
(4).不是奇函数,也不是偶函数;
(5).当a>1时,函数在R上单调递增;当0<a<1时,函数在R上单调递减;
(6).函数图象无限靠近x轴;
(7).当a>1时,随着a的增大,函数图象在第一象限越来越靠近y轴;当0<a<1时,随着a的减小,函数图象在第二象限越来越靠近y轴.
学生发言的同时,教师及时板书.
2.
教师引导学生回忆并观察自己画出的与、与或
与的图象,说说底数互为倒数的两个函数图象间有没有什么关系.
学生发表自己的观点后,教师动态展示与的函数图象关于y轴对称.
教师引导学生猜想与且的图象是否关于y轴对称?
板书上述性质,并鼓励学有余力的学生课后做出严格证明.
(这正体现了新课标中不同的学生在数学上得到不同的发展这一理念)
活动五
新知应用
已知指数函数f(x)=ax
(a>0且a≠1)的图象过点,求f(0),
f(1),
f(-3)的值.
学生独立练习,教师个别指导.结束后,请一位学生口述解题过程,教师实施评价并展示解题过程.
解:因为的图象过点,所以
,
即,解得,于是
.
所以,
活动六
小结归纳
布置作业
教师提问:通过这节课的学习,你有哪些收获呢?
1.知识:
2.数学史:
(教师在本环节先引导学生从知识层面对指数函数及其性质进行梳理,深化知识与技能,回顾课堂中认识到的数学人物庄子和华罗庚,旨在渗透数学史并且增强学生的民族自豪感.)
作业
必做:习题2.1
A组5、6题
选做:查阅关于“富兰克林的遗嘱和拿破仑的诺言”相关资料,写一篇不
少于300字的小论文,体会并与同伴交流指数函数在生活中的应用.
(选做题的加入,一方面是让学生体会数学的应用价值,提高资料检索的能力,另一方面体现了不同的学生在数学上得到不同的发展这一理念.)
板书设计
§2.1.2
指数函数及其性质
多媒体
当a=0,
……
当a>0,
……
当a<0,
……
a>1
0定义域:
值
域:
恒过点:
单调性:
奇偶性:
《§2.1.2
指数函数及其性质》教学设计
课
题
§2.1.2
指数函数及其性质
(第一课时)
教材版本
人民教育出版社普通高中课程标准实验教科书数学必修1
A版
教学目标
1.
通过实例引入指数函数,激发学生的学习兴趣,体会指数函数是一类重要的函数模型,体会数学的应用价值;
2.
通过牛肉面的实例,激发学生对家乡的热爱之情;
3.
通过探究指数函数的底数a的条件,明确数学概念的严谨性和科学性,并领会分类讨论的思想方法;
4.
掌握指数函数的概念,并能根据定义判断一个函数是否为指数函数;
5.
通过现代信息技术的合理利用,让学生体会到现代信息技术是认识世界的有效手段;
6.
通过观察指数函数的图象,分析、归纳、总结、自主建构指数函数的性质;
7.
体会数形结合的思想,培养学生发现、分析、解决问题的能力;
8.
在探究过程中,让学生体会从特殊到一般的数学方法;
9.
会用指数函数及其性质解决指数函数相关问题.
教学重点
指数函数的概念和性质.
教学难点
用数形结合的方法从具体到一般地探索、概括指数函数的性质.
授课类型
新授课
课时安排
第一课时(40分钟)
教学方法
引导启发式、参与发现式
教学用具
多媒体课件、坐标纸、性质列表.
教学过程
活动一
体会身边的指数模型
1.教师请学生展示牛肉面的拉面过程,让学生抽象出拉面师两手之间的面的根数与对折次数之间的关系.
(设计牛肉面的情境,旨在激起学生学习数学的热情,调动学生主体参与学习活动的积极性,并让学生体会身边的指数模型,同时感受家乡美.)
2.庄子在《天下篇》中说:“一尺之棰,日取其半,万世不竭.”请学生写出截取第x次后,木棰的剩留量y与x的关系式.
(设计这个情境,旨在渗透数学史.)
3.回顾两个情境,教师提问情境中涉及到的两个关系式和是不是函数,为指数函数定义的探究做好铺垫.
活动二
探究指数函数的定义
1.将活动一得到的关系式中的定义域扩充到实数集范围,即.提问学生上述关系式是否为函数?
2.如果将中的底数2替换为常数a,它还是函数吗?
学生分小组讨论,教师引导学生对参数a的限定条件进行讨论,得出且的结论.
教师也参与到学生的讨论中,对有困难的小组进行启发.
(采用小组合作这种方式,一方面是考虑到小组合作这种特殊的学习模式具有信息密度大、传递速度快等特点,另一方面是为了培养学生的合作意识和语言表达能力,让学生尝试“说数学”.)
3.讨论结束后,小组派代表向全班同学展示讨论结果.
(学生发表观点,教师及时实施多元评价.)
交流后,教师完善定义并用多媒体展示指数函数定义,并指出指数函数的定义是形式化的定义,我们必须严格依照它的形式来判断一个函数是否为指数函数.并用多媒体展示形式中的三个要求.
一般地,函数y=ax(a>0,且a≠1)叫做指数函数(exponential
function),其中x是自变量,函数的定义域是R.
想一想
下列四个函数是不是指数函数?
教师随机提问.
(这个环节是为了让学生进一步理解指数函数的形式化定义.)
活动三
探究指数函数的图象
学生活动1
分小组在事先准备好的坐标纸上用描点法作出下面几个指数函数的图象.
与;与;与.
要求:每位同学从上述三组函数中选择一组底数互为倒数的指数函数作出函数的图象.
(设置这个环节是为了让学生尝试“做数学”,体会知识的生成过程,教师对有困难的同学进行个别指导.)
学生活动2
选代表展示自己画出的图象.教师给予及时评价.
(教师鼓励性的及时评价有利于学生建立学习数学、探索知识的自信心.)
展示交流后,教师用几何画板作出第一组的两个图象,再用EXCEL画出第二组和第三组的4个函数图象.并请学生对比自己画出的图象.
教师进一步用几何画板展示当底数且为任意常数时对应的指数函数的图象.
(EXCEL和几何画板的加入,有利于学生更准确地认识指数函数的图象,节省课堂有效教学时间,同时也体现了信息技术的有效整合.)
活动四
探究指数函数的性质
1.教师结合几何画板,动态呈现底数a变化时的一系列函数图象,让学生仔细观察图象特征,进而归纳相应性质.学生积极发言.
学情预设
(1).定义域是R;
(2).图象恒过(0,1)点;
(3).值域是(0,+∞);
(4).不是奇函数,也不是偶函数;
(5).当a>1时,函数在R上单调递增;当0<a<1时,函数在R上单调递减;
(6).函数图象无限靠近x轴;
(7).当a>1时,随着a的增大,函数图象在第一象限越来越靠近y轴;当0<a<1时,随着a的减小,函数图象在第二象限越来越靠近y轴.
学生发言的同时,教师及时板书.
2.
教师引导学生回忆并观察自己画出的与、与或
与的图象,说说底数互为倒数的两个函数图象间有没有什么关系.
学生发表自己的观点后,教师动态展示与的函数图象关于y轴对称.
教师引导学生猜想与且的图象是否关于y轴对称?
板书上述性质,并鼓励学有余力的学生课后做出严格证明.
(这正体现了新课标中不同的学生在数学上得到不同的发展这一理念)
活动五
新知应用
已知指数函数f(x)=ax
(a>0且a≠1)的图象过点,求f(0),
f(1),
f(-3)的值.
学生独立练习,教师个别指导.结束后,请一位学生口述解题过程,教师实施评价并展示解题过程.
解:因为的图象过点,所以
,
即,解得,于是
.
所以,
活动六
小结归纳
布置作业
教师提问:通过这节课的学习,你有哪些收获呢?
1.知识:
2.数学史:
(教师在本环节先引导学生从知识层面对指数函数及其性质进行梳理,深化知识与技能,回顾课堂中认识到的数学人物庄子和华罗庚,旨在渗透数学史并且增强学生的民族自豪感.)
作业
必做:习题2.1
A组5、6题
选做:查阅关于“富兰克林的遗嘱和拿破仑的诺言”相关资料,写一篇不
少于300字的小论文,体会并与同伴交流指数函数在生活中的应用.
(选做题的加入,一方面是让学生体会数学的应用价值,提高资料检索的能力,另一方面体现了不同的学生在数学上得到不同的发展这一理念.)
板书设计
§2.1.2
指数函数及其性质
多媒体
当a=0,
……
当a>0,
……
当a<0,
……
a>1
0
值
域:
恒过点:
单调性:
奇偶性:
