五年级上册数学课件-第六单元第4课时 公顷、平方千米(2) 北师大版(共28张PPT)
文档属性
| 名称 | 五年级上册数学课件-第六单元第4课时 公顷、平方千米(2) 北师大版(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 07:31:19 | ||
图片预览





文档简介
五年级数学上册教学课件(北师版)
第六单元 组合图形的面积
第四课时 公顷、平方千米(2)
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
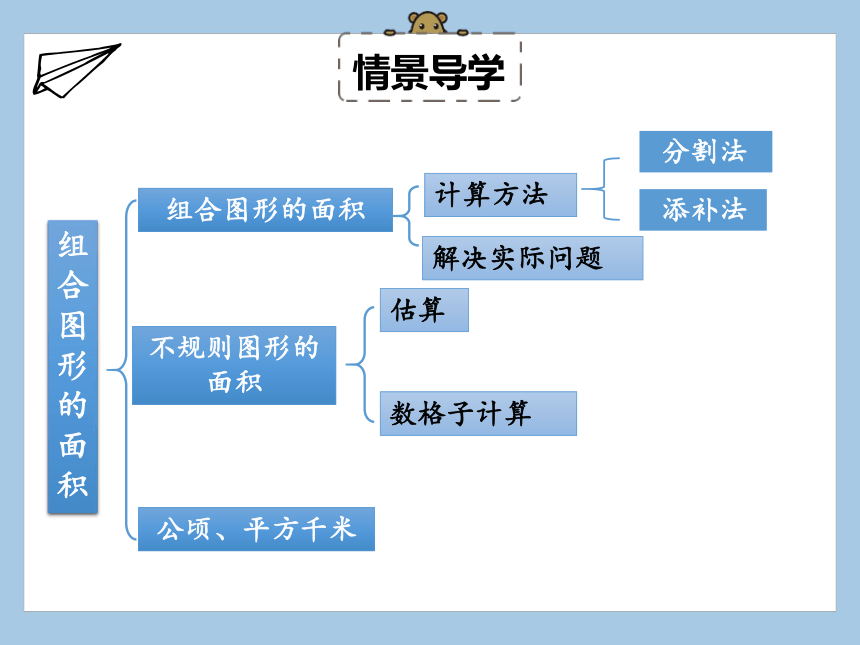
组合图形的面积
组合图形的面积
不规则图形的面积
公顷、平方千米
计算方法
解决实际问题
估算
数格子计算
分割法
添补法
探索与发现
02
探索与发现
求组合图形的面积时,要把图形的面积转化成几个已经学过的图形的面积的和或差,同时要找准题中的已知数据,从而顺利求出面积。常用的求组合图形的面积的方法有:分割法、添补法、割补法等。
1.组合图形面积的求法
探索与发现
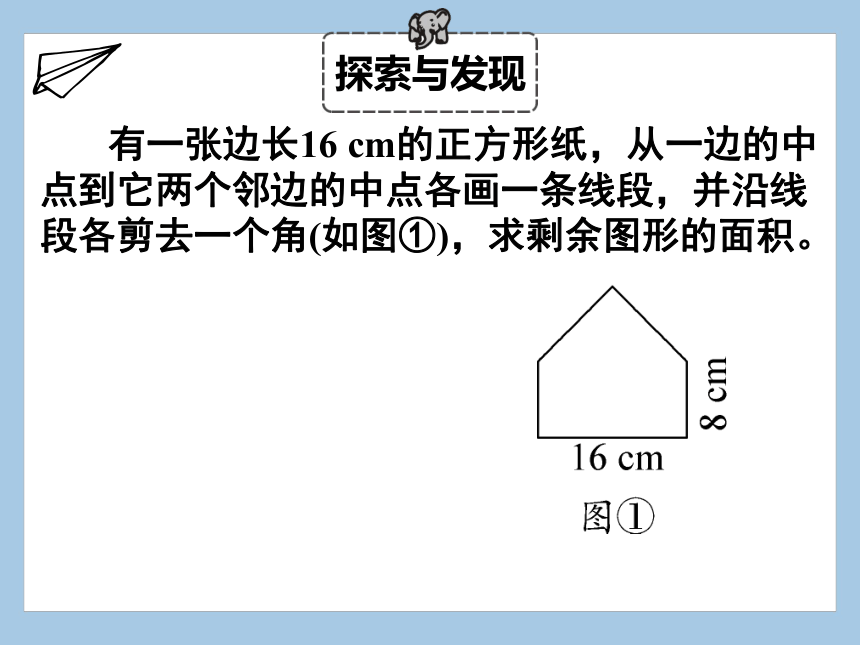
有一张边长16 cm的正方形纸,从一边的中点到它两个邻边的中点各画一条线段,并沿线段各剪去一个角(如图①),求剩余图形的面积。
探索与发现
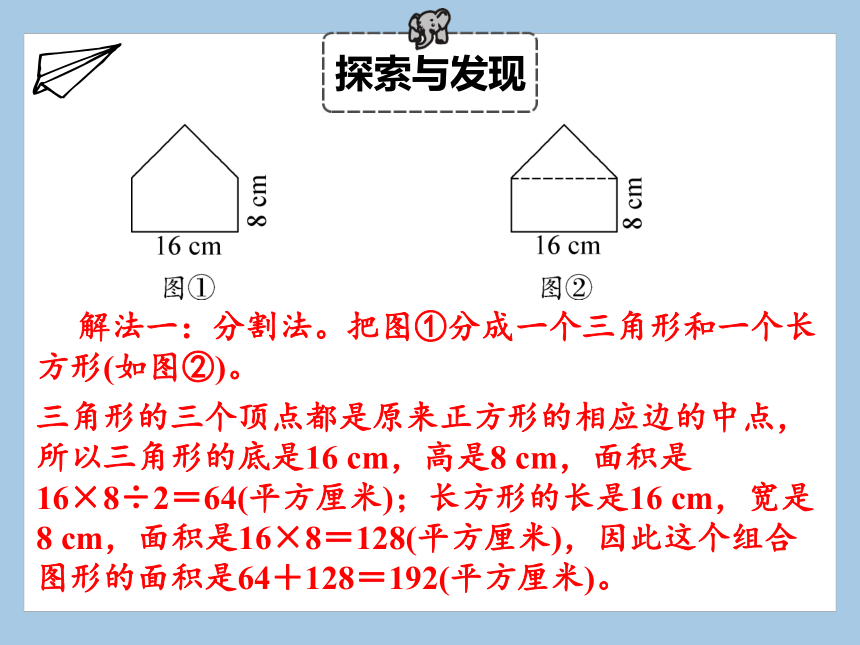
三角形的三个顶点都是原来正方形的相应边的中点,所以三角形的底是16 cm,高是8 cm,面积是16×8÷2=64(平方厘米);长方形的长是16 cm,宽是8 cm,面积是16×8=128(平方厘米),因此这个组合图形的面积是64+128=192(平方厘米)。
解法一:分割法。把图①分成一个三角形和一个长方形(如图②)。
探索与发现
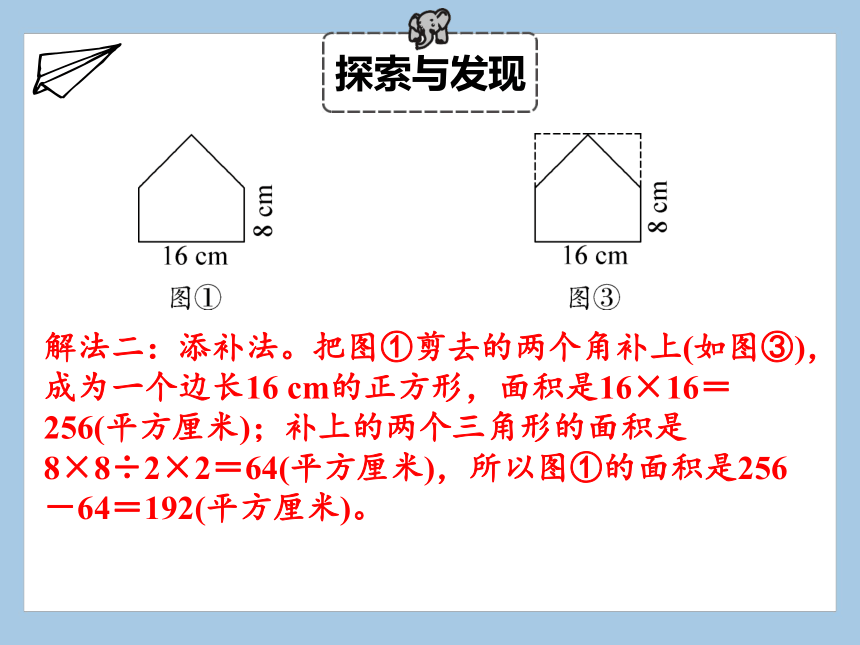
解法二:添补法。把图①剪去的两个角补上(如图③),成为一个边长16 cm的正方形,面积是16×16=256(平方厘米);补上的两个三角形的面积是
8×8÷2×2=64(平方厘米),所以图①的面积是256-64=192(平方厘米)。
探索与发现
解法三:割补法。将图①上面的三角形沿着高分成两个小三角形,然后把这两个小三角形割下来,补到下面长方形的右边(如图④),就可以得到一个长为16+8=24(厘米),宽为8 cm的长方形,所以图①的面积是24×8=192(平方厘米)。
探索与发现
2.估计图形的面积
(1)可以采用数格子(边长1 cm的方格)的方法,数格子时,不满一格的可按半格来数。
(2)还可根据图形确定近似基本图,量出基本图中可用于计算面积的长度,进而算出面积。
探索与发现
3.公顷、平方千米
(1)公顷:边长为100 m的正方形土地的面积,1公顷的土地为10000 m2,相当与一个标准足球场的面积。
(2)平方千米:边长为1000 m的正方形土地的面积,1平方千米的土地为1000000 m2,“平方千米”是比“公顷”还要大的面积单位,计算较大的土地面积一般用“平方千米”作单位。例如:我国的陆地面积大约是960万平方千米。
探索与发现
3.公顷、平方千米
(3)平方米、公顷、平方千米之间的关系:
1公顷=10000 m2 1 km2=100公顷
探索与发现
4.购票方案与租车问题
(1)购票方案的确定:可根据人数的多少,价格的不同以及团体及优惠人数的多少,合理选择一种方案购票或几种方案结合起来购票。
(2)合理租车方案的确定:在游客人数、车辆类型、限乘人数、每辆车的价格确定后,还要使车辆空位尽量少。租车时,可以租同一类型的,也可以混合租车,然后算出总租金,比较后,找出最合适的方案。
探索与发现
一个由两个家庭共10人(8个大人,2个小孩)组成的旅行团去某景点旅游,怎么购票最省钱?
个人票
团体票
成人 60元/人
儿童 20元/人
8人及以上
45元/人
探索与发现
个人票
团体票
成人 60元/人
儿童 20元/人
8人及以上
45元/人
根据条件可知,有三种方案购票。
分析
买个人票需要的钱数是:60×8+20×2=520(元)
买团体票需要的钱数是:45×10=450(元)
两种方式混合购票最少需要的钱数是:45×8+20×2=400(元)
所以两种方案混合购票最省钱。
探索与发现
5.图形中的规律
在观察图形时,要根据已知图形的前、后(或上、下)之间的关系,找出其中的规律,推导出后面的图形。
探索与发现
6.尝试与猜想
在用列表法进行尝试与猜想时,一般采取逐一列表法,为了减少尝试的次数,也可以先估计可能的范围,再用列表举例法,还可以采用取中列表法。
例如:停车场上停着小轿车和摩托车共28辆,这些车共有82个轮子。停车场上有小轿车和摩托车各多少辆?
探索与发现
(1)逐一列表法。
小轿车/辆
摩托车/辆
轮子数/个
1
27
58
2
26
60
3
25
62
4
24
64
…
…
…
13
15
82
即小轿车有13辆,摩托车有15辆。
停车场上停着小轿车和摩托车共28辆,这些车共有82个轮子。停车场上有小轿车和摩托车各多少辆?
分析
探索与发现
(2)先估计可能的范围,再用列表举例法。逐一举例时,为了减少举例的次数,可以先估计小轿车和摩托车数量的可能范围,再列表寻找问题的结果。如右表:
小轿车/辆
摩托车/辆
轮子数/个
1
27
58
5
23
66
10
18
76
15
13
86
14
14
84
13
15
82
分析
探索与发现
……轮子个数少了,说明小轿车数量少了。
……轮子个数还少,小轿车还应该增加。
……比82多了,小轿车应该在10和15之间。
即小轿车有13辆,摩托车有15辆。
停车场上停着小轿车和摩托车共28辆,这些车共有82个轮子。停车场上有小轿车和摩托车各多少辆?
分析
探索与发现
计算右边组合图形的面积。
上图是由一个平行四边形和一个三角形组成的组合图形,三角形和平行四边形的底是相同的,高已知,运用面积计算公式求解。
8×4+8×3÷2=44(平方厘米)
分析
探索与发现
仔细观察点阵,在括号里填上适当的算式,并在后面的方框里接着画一画。
探索与发现
观察点阵可以发现,第一个点阵有1个点,第二个点阵比第一个点阵多了2个点,所以有1+2=3(个)点,第三个点阵比第二个多了3个点,所以是1+2+3=6(个)点。同理,第四个点阵是1+2+3+4=10(个)点,第五个点阵是1+2+3+4+5=15(个)点。
分析
探索与发现
解答:
1+2+3 1+2+3+4 1+2+3+4+5
仔细观察点阵,在括号里填上适当的算式,并在后面的方框里接着画一画。
课后作业
03
完成《导学案》同步练习。
课后作业
感 谢 观 看
第六单元 组合图形的面积
第四课时 公顷、平方千米(2)
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
组合图形的面积
组合图形的面积
不规则图形的面积
公顷、平方千米
计算方法
解决实际问题
估算
数格子计算
分割法
添补法
探索与发现
02
探索与发现
求组合图形的面积时,要把图形的面积转化成几个已经学过的图形的面积的和或差,同时要找准题中的已知数据,从而顺利求出面积。常用的求组合图形的面积的方法有:分割法、添补法、割补法等。
1.组合图形面积的求法
探索与发现
有一张边长16 cm的正方形纸,从一边的中点到它两个邻边的中点各画一条线段,并沿线段各剪去一个角(如图①),求剩余图形的面积。
探索与发现
三角形的三个顶点都是原来正方形的相应边的中点,所以三角形的底是16 cm,高是8 cm,面积是16×8÷2=64(平方厘米);长方形的长是16 cm,宽是8 cm,面积是16×8=128(平方厘米),因此这个组合图形的面积是64+128=192(平方厘米)。
解法一:分割法。把图①分成一个三角形和一个长方形(如图②)。
探索与发现
解法二:添补法。把图①剪去的两个角补上(如图③),成为一个边长16 cm的正方形,面积是16×16=256(平方厘米);补上的两个三角形的面积是
8×8÷2×2=64(平方厘米),所以图①的面积是256-64=192(平方厘米)。
探索与发现
解法三:割补法。将图①上面的三角形沿着高分成两个小三角形,然后把这两个小三角形割下来,补到下面长方形的右边(如图④),就可以得到一个长为16+8=24(厘米),宽为8 cm的长方形,所以图①的面积是24×8=192(平方厘米)。
探索与发现
2.估计图形的面积
(1)可以采用数格子(边长1 cm的方格)的方法,数格子时,不满一格的可按半格来数。
(2)还可根据图形确定近似基本图,量出基本图中可用于计算面积的长度,进而算出面积。
探索与发现
3.公顷、平方千米
(1)公顷:边长为100 m的正方形土地的面积,1公顷的土地为10000 m2,相当与一个标准足球场的面积。
(2)平方千米:边长为1000 m的正方形土地的面积,1平方千米的土地为1000000 m2,“平方千米”是比“公顷”还要大的面积单位,计算较大的土地面积一般用“平方千米”作单位。例如:我国的陆地面积大约是960万平方千米。
探索与发现
3.公顷、平方千米
(3)平方米、公顷、平方千米之间的关系:
1公顷=10000 m2 1 km2=100公顷
探索与发现
4.购票方案与租车问题
(1)购票方案的确定:可根据人数的多少,价格的不同以及团体及优惠人数的多少,合理选择一种方案购票或几种方案结合起来购票。
(2)合理租车方案的确定:在游客人数、车辆类型、限乘人数、每辆车的价格确定后,还要使车辆空位尽量少。租车时,可以租同一类型的,也可以混合租车,然后算出总租金,比较后,找出最合适的方案。
探索与发现
一个由两个家庭共10人(8个大人,2个小孩)组成的旅行团去某景点旅游,怎么购票最省钱?
个人票
团体票
成人 60元/人
儿童 20元/人
8人及以上
45元/人
探索与发现
个人票
团体票
成人 60元/人
儿童 20元/人
8人及以上
45元/人
根据条件可知,有三种方案购票。
分析
买个人票需要的钱数是:60×8+20×2=520(元)
买团体票需要的钱数是:45×10=450(元)
两种方式混合购票最少需要的钱数是:45×8+20×2=400(元)
所以两种方案混合购票最省钱。
探索与发现
5.图形中的规律
在观察图形时,要根据已知图形的前、后(或上、下)之间的关系,找出其中的规律,推导出后面的图形。
探索与发现
6.尝试与猜想
在用列表法进行尝试与猜想时,一般采取逐一列表法,为了减少尝试的次数,也可以先估计可能的范围,再用列表举例法,还可以采用取中列表法。
例如:停车场上停着小轿车和摩托车共28辆,这些车共有82个轮子。停车场上有小轿车和摩托车各多少辆?
探索与发现
(1)逐一列表法。
小轿车/辆
摩托车/辆
轮子数/个
1
27
58
2
26
60
3
25
62
4
24
64
…
…
…
13
15
82
即小轿车有13辆,摩托车有15辆。
停车场上停着小轿车和摩托车共28辆,这些车共有82个轮子。停车场上有小轿车和摩托车各多少辆?
分析
探索与发现
(2)先估计可能的范围,再用列表举例法。逐一举例时,为了减少举例的次数,可以先估计小轿车和摩托车数量的可能范围,再列表寻找问题的结果。如右表:
小轿车/辆
摩托车/辆
轮子数/个
1
27
58
5
23
66
10
18
76
15
13
86
14
14
84
13
15
82
分析
探索与发现
……轮子个数少了,说明小轿车数量少了。
……轮子个数还少,小轿车还应该增加。
……比82多了,小轿车应该在10和15之间。
即小轿车有13辆,摩托车有15辆。
停车场上停着小轿车和摩托车共28辆,这些车共有82个轮子。停车场上有小轿车和摩托车各多少辆?
分析
探索与发现
计算右边组合图形的面积。
上图是由一个平行四边形和一个三角形组成的组合图形,三角形和平行四边形的底是相同的,高已知,运用面积计算公式求解。
8×4+8×3÷2=44(平方厘米)
分析
探索与发现
仔细观察点阵,在括号里填上适当的算式,并在后面的方框里接着画一画。
探索与发现
观察点阵可以发现,第一个点阵有1个点,第二个点阵比第一个点阵多了2个点,所以有1+2=3(个)点,第三个点阵比第二个多了3个点,所以是1+2+3=6(个)点。同理,第四个点阵是1+2+3+4=10(个)点,第五个点阵是1+2+3+4+5=15(个)点。
分析
探索与发现
解答:
1+2+3 1+2+3+4 1+2+3+4+5
仔细观察点阵,在括号里填上适当的算式,并在后面的方框里接着画一画。
课后作业
03
完成《导学案》同步练习。
课后作业
感 谢 观 看
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
