人教版数学七年级上册1.5科学记数法和近似数课件(31张)
文档属性
| 名称 | 人教版数学七年级上册1.5科学记数法和近似数课件(31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-18 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
科学记数法和近似数
新知引入
太阳半径约696
000千米
光速约300
000
000米/秒
读一读这些数
用科学记数法表示数
1
世界人口约
7
700
000
000人
新知引入
(1)地球离太阳约有1.5亿公里.
(2)第六次人口普查时,中国人口约为1
400
000
000人.
(3)地球上煤的储量估计15万亿吨以上.
在生活中我们还会遇到一些比较大的数.例如:
像这样较大的数据,书写和阅读都有一定困难,那么有没有这样一种表示方法,使得这些大数易写,易读呢?
新知引入
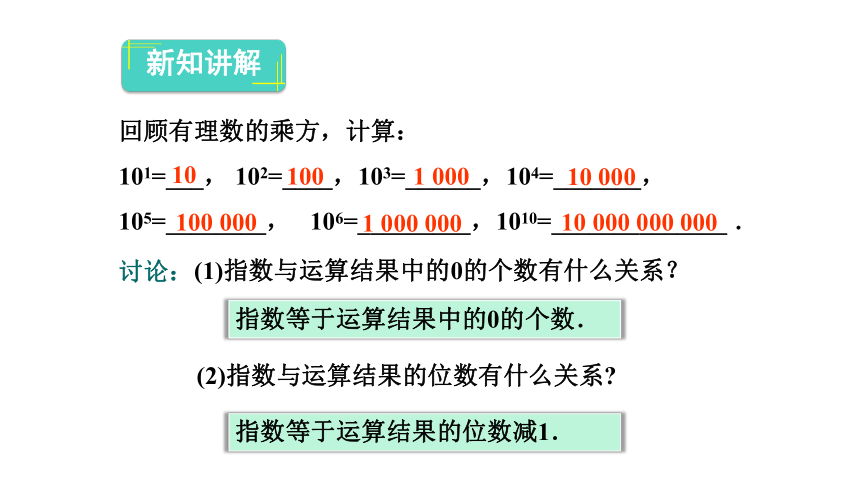
回顾有理数的乘方,计算:
101=___,
102=____,103=______,104=_______,105=________,
106=_________,1010=______________
.
10
100
1
000
10
000
100
000
1
000
000
10
000
000
000
新知讲解
指数等于运算结果中的0的个数.
指数等于运算结果的位数减1.
(1)指数与运算结果中的0的个数有什么关系?
(2)指数与运算结果的位数有什么关系?
讨论:
试一试
1.把下列各数写成10的幂的形式:
100
,1
000,10
000,
2.300=3×100=3×10(
)
3
000=3×1
000=3×10
(
)
30
000=3×10
000=3×10
(
)
新知讲解
102
103
104
2
3
4
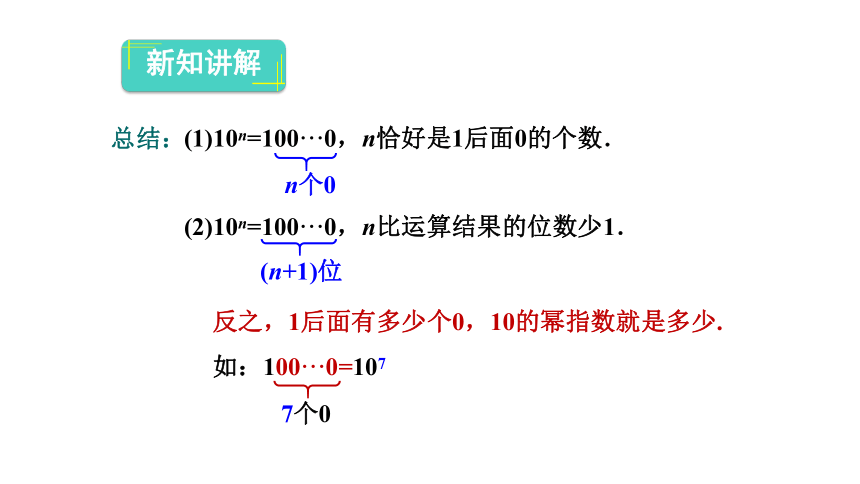
反之,1后面有多少个0,10的幂指数就是多少.
新知讲解
(1)10n=100···0,n恰好是1后面0的个数.
(2)10n=100···0,n比运算结果的位数少1.
n个0
(n+1)位
总结:
如:100···0=107
7个0
科学记数法定义:
把一个大于10的数表示成a×10n(其中1≤|a|<10,n为正整数),这种形式的记数方法叫做科学记数法.
对于小于-10的数也可以类似表示.例如:
-567
000
000=
×100
000
000=
.
-5.67×108
-5.67
新知讲解
例1
用科学记数法表示下列各数:
1
000
000,57
000
000,-123
000
000
000
解:1
000
000=106
57
000
000=5.7×107
-123
000
000
000=-1.23×1011
归纳:用科学记数法表示一个n位整数时,
10的指数是______.
n-1
新知应用
【变式】1.用科学记数法表示下列各数.
8万
-70
410
000
6
700
000
新知演练
解:
8万=8×104
-70
410
000=-7.041×107
6
700
000=6.7×106
2.在以下各数中,最大的数为(
)
A.7.2×105
B.2.5×106
C.9.9×105
D.1×107
D
(1)2003年10月15日,中国首次进行载人航天飞行,神舟五号飞船绕地球飞行了14圈,行程约为6×105千米.
(2)一套《辞海》大约有1.7×107个字.
新知应用
例2
下列用科学记数法表示的数,原数是什么?
解:6×105=600
000
解:1.7×107=17
000
000
(3)1972年3月发射的“先驱者十号”是人类发往太阳系外的第一艘人造太空探测器,至2003年2
月人们最后一次收到它发回的信号时,它离地球1.22×1011千米.
新知应用
例2
下列用科学记数法表示的数,原数是什么?
解:1.22×1011=122
000
000
000
归纳:反过来,如果用科学记数法表示的数10的指数是n,
那么原数有n+1位整数位.
【变式】1.6.74×105的原数有____位整数;
-3.251×107原数有____位整数;
9.6104×1012原数有____位整数.
6
8
13
新知演练
2.下列用科学记数法表示的数,原来各是什么数?
4×103
8.5×106
7.04×105
3.96×104
4
000
8
500
000
704
000
39
600
【变式】3.废旧电池对环境的危害十分巨大,一粒纽扣电池能污染600立方米的水(相当于一个人一生的饮水量).某班有50名学生,如果每名学生一年丢弃一粒纽扣电池,且都没有被回收,那么被该班学生一年丢弃的纽扣电池能污染的水量用科学记数法表示为__________立方米.
3×104
解析:600×50=30
000=3×104(立方米)
新知演练
北京地铁1号线是我国最早的地铁路线,全长31.04公里.
“31.04”一定是准确的数据吗?
新知引入
不是
近似数
2
下列语句中,哪些数据是精确的,哪些数据是近似的?
1.妈妈去买水果,买了
8
个苹果,大约
3
千克.
2.小民与小李买了
2
瓶水,4
根黄瓜,6
袋香巴拉牛肉干,约
20
元,然后骑车去大约
3.5
km外去郊游,大约玩了
4.5
小时回家.
3.我国共有
56
个民族.
精确数:8,2,4,6,56;
近似数:3,20,3.5和4.5.
新知讲解
问题:什么样的数是近似数?你能举例说明吗?
1.我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数.例如,姚明的身高是2.26米.
新知讲解
2.有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数.例如,××年全国高考报名的考生共940万人.
准确数是完全符合实际的数;近似数是与实际接近的数.
3
小明和小颖分别测量了同一片树叶的长度,他们所用的直尺的最小单位是不同的,分别是厘米和毫米.
问题:根据小明的测量,这片树叶的长度约为多少?
根据小颖的测量呢?谁的测量结果会更精确一些?
小明
小颖
0
2
3
4
5
1
0
1
2
3
4
5
新知讲解
3厘米
3.2厘米
小颖测量结果更精确.
近似数是一个与准确数接近的数,其接近程度可以用精确度表示.
说一说:小明、小颖的测量分别精确到什么单位?
新知讲解
小明精确到厘米;小颖精确到毫米.
π≈3(精确到
位),
π≈3.1(精确到
,或叫做精确到
),
π≈3.14(精确到
,或叫精确到
),
π≈3.140(精确到
,或叫做精确到
),
π≈3.141
6(精确到
,或叫做精确到
),
……
按四舍五入法对圆周率π取近似数,有:
新知讲解
个
0.1
十分位
0.01
百分位
0.001
千分位
0.000
1
万分位
1.下列数据中,不是近似数的是(
)
A.某次地震中,伤亡10万人
B.吐鲁番盆地低于海平面155m
C.小明班上有45人
D.小红测得数学书的长度为21.0cm
C
跟踪练习
2.下列结论正确的是(
)
A.近似数4.230和4.23的精确度是一样的
B.近似数89.0是精确到个位
C.近似数0.005
10与0.051
0的精确度不一样
D.近似数6万与近似数60
000的精确度相同
C
跟踪练习
解:(1)0.015
8
≈0.016;(2)304.35≈304;
(3)1.804
≈1.8;
(4)1.804≈1.80.
(4)中能把1.80后面的0去掉吗?
对8四舍五入
对3四舍五入
对0四舍五入
对4四舍五入
新知应用
例3
按括号内的要求,用四舍五入法对下列各数取近似数:
(1)0.015
8(精确到0.001);
(2)304.35(精确到个位);
(3)1.804(精确到0.1);
(4)1.804(精确到0.01).
新知演练
【变式】用四舍五入法按要求取近似值:
(1)75
436(精确到百位)
(2)0.785(精确到百分位)
解:(1)75
436≈7.54×104
(2)0.785≈0.79
解:(1)600万,精确到万位;
(2)7.03万,精确到百位;
(3)5.8亿,精确到千万位;
(4)3.30×105,精确到千位.
先把数还原,再看3所在的数位.
新知应用
例4
下列由四舍五入得到的近似数,各精确到哪一位?
(1)600万;
(2)7.03万;
(3)5.8亿;
(4)3.30×105.
解:(1)精确到0.01
(2)精确到万位
(3)精确到0.00001
新知演练
【变式】下列数据精确到什么位?
(1)小王的身高1.53米;
(2)月球与地球相距38万千米;
(3)圆周率π取3.14159.
解:
从5月1日至10月31日共有184天,
故每天的平均入园人次为:
7308.44÷184≈39.719≈39.72(万人次).
新知应用
例5
据2010年上海世博会官方统计,2010年5月1日至10月31日期间,共有7308.44万人次入园参观,求每天平均入园人次(精确到0.01万人次).
拓展练习
1.生物学指出,生态系数中,每输入一个营养级的能量,大约只有10%的能量能够流动到下一个营养级,在H1→H2→H3→H4→H5→H6这条生物链中要使H6获得10千焦的能量,则需要H1提供的能量为多少?
解:10×100
000=1
000
000=106(千焦).
2.近似数1.70所表示的准确值a的范围是(
)
A.1.700<a≤1.705
B.1.60≤a<1.80
C.1.64<a≤1.705
D.1.695≤a<1.705
拓展练习
D
科学记数法:
用科学记数法表示较大的数应注意以下两点:
?1≤a<10;
?当大数是大于10的整数时,n为整数位减去1.
课堂总结
近似数:
1.判断准确数与近似数.
2.按照要求取近似数.
四舍五入到某一位,就说这个数的近似数精确到那一位.
3.由近似数判断精确度.
课堂总结
科学记数法和近似数
新知引入
太阳半径约696
000千米
光速约300
000
000米/秒
读一读这些数
用科学记数法表示数
1
世界人口约
7
700
000
000人
新知引入
(1)地球离太阳约有1.5亿公里.
(2)第六次人口普查时,中国人口约为1
400
000
000人.
(3)地球上煤的储量估计15万亿吨以上.
在生活中我们还会遇到一些比较大的数.例如:
像这样较大的数据,书写和阅读都有一定困难,那么有没有这样一种表示方法,使得这些大数易写,易读呢?
新知引入
回顾有理数的乘方,计算:
101=___,
102=____,103=______,104=_______,105=________,
106=_________,1010=______________
.
10
100
1
000
10
000
100
000
1
000
000
10
000
000
000
新知讲解
指数等于运算结果中的0的个数.
指数等于运算结果的位数减1.
(1)指数与运算结果中的0的个数有什么关系?
(2)指数与运算结果的位数有什么关系?
讨论:
试一试
1.把下列各数写成10的幂的形式:
100
,1
000,10
000,
2.300=3×100=3×10(
)
3
000=3×1
000=3×10
(
)
30
000=3×10
000=3×10
(
)
新知讲解
102
103
104
2
3
4
反之,1后面有多少个0,10的幂指数就是多少.
新知讲解
(1)10n=100···0,n恰好是1后面0的个数.
(2)10n=100···0,n比运算结果的位数少1.
n个0
(n+1)位
总结:
如:100···0=107
7个0
科学记数法定义:
把一个大于10的数表示成a×10n(其中1≤|a|<10,n为正整数),这种形式的记数方法叫做科学记数法.
对于小于-10的数也可以类似表示.例如:
-567
000
000=
×100
000
000=
.
-5.67×108
-5.67
新知讲解
例1
用科学记数法表示下列各数:
1
000
000,57
000
000,-123
000
000
000
解:1
000
000=106
57
000
000=5.7×107
-123
000
000
000=-1.23×1011
归纳:用科学记数法表示一个n位整数时,
10的指数是______.
n-1
新知应用
【变式】1.用科学记数法表示下列各数.
8万
-70
410
000
6
700
000
新知演练
解:
8万=8×104
-70
410
000=-7.041×107
6
700
000=6.7×106
2.在以下各数中,最大的数为(
)
A.7.2×105
B.2.5×106
C.9.9×105
D.1×107
D
(1)2003年10月15日,中国首次进行载人航天飞行,神舟五号飞船绕地球飞行了14圈,行程约为6×105千米.
(2)一套《辞海》大约有1.7×107个字.
新知应用
例2
下列用科学记数法表示的数,原数是什么?
解:6×105=600
000
解:1.7×107=17
000
000
(3)1972年3月发射的“先驱者十号”是人类发往太阳系外的第一艘人造太空探测器,至2003年2
月人们最后一次收到它发回的信号时,它离地球1.22×1011千米.
新知应用
例2
下列用科学记数法表示的数,原数是什么?
解:1.22×1011=122
000
000
000
归纳:反过来,如果用科学记数法表示的数10的指数是n,
那么原数有n+1位整数位.
【变式】1.6.74×105的原数有____位整数;
-3.251×107原数有____位整数;
9.6104×1012原数有____位整数.
6
8
13
新知演练
2.下列用科学记数法表示的数,原来各是什么数?
4×103
8.5×106
7.04×105
3.96×104
4
000
8
500
000
704
000
39
600
【变式】3.废旧电池对环境的危害十分巨大,一粒纽扣电池能污染600立方米的水(相当于一个人一生的饮水量).某班有50名学生,如果每名学生一年丢弃一粒纽扣电池,且都没有被回收,那么被该班学生一年丢弃的纽扣电池能污染的水量用科学记数法表示为__________立方米.
3×104
解析:600×50=30
000=3×104(立方米)
新知演练
北京地铁1号线是我国最早的地铁路线,全长31.04公里.
“31.04”一定是准确的数据吗?
新知引入
不是
近似数
2
下列语句中,哪些数据是精确的,哪些数据是近似的?
1.妈妈去买水果,买了
8
个苹果,大约
3
千克.
2.小民与小李买了
2
瓶水,4
根黄瓜,6
袋香巴拉牛肉干,约
20
元,然后骑车去大约
3.5
km外去郊游,大约玩了
4.5
小时回家.
3.我国共有
56
个民族.
精确数:8,2,4,6,56;
近似数:3,20,3.5和4.5.
新知讲解
问题:什么样的数是近似数?你能举例说明吗?
1.我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数.例如,姚明的身高是2.26米.
新知讲解
2.有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数.例如,××年全国高考报名的考生共940万人.
准确数是完全符合实际的数;近似数是与实际接近的数.
3
小明和小颖分别测量了同一片树叶的长度,他们所用的直尺的最小单位是不同的,分别是厘米和毫米.
问题:根据小明的测量,这片树叶的长度约为多少?
根据小颖的测量呢?谁的测量结果会更精确一些?
小明
小颖
0
2
3
4
5
1
0
1
2
3
4
5
新知讲解
3厘米
3.2厘米
小颖测量结果更精确.
近似数是一个与准确数接近的数,其接近程度可以用精确度表示.
说一说:小明、小颖的测量分别精确到什么单位?
新知讲解
小明精确到厘米;小颖精确到毫米.
π≈3(精确到
位),
π≈3.1(精确到
,或叫做精确到
),
π≈3.14(精确到
,或叫精确到
),
π≈3.140(精确到
,或叫做精确到
),
π≈3.141
6(精确到
,或叫做精确到
),
……
按四舍五入法对圆周率π取近似数,有:
新知讲解
个
0.1
十分位
0.01
百分位
0.001
千分位
0.000
1
万分位
1.下列数据中,不是近似数的是(
)
A.某次地震中,伤亡10万人
B.吐鲁番盆地低于海平面155m
C.小明班上有45人
D.小红测得数学书的长度为21.0cm
C
跟踪练习
2.下列结论正确的是(
)
A.近似数4.230和4.23的精确度是一样的
B.近似数89.0是精确到个位
C.近似数0.005
10与0.051
0的精确度不一样
D.近似数6万与近似数60
000的精确度相同
C
跟踪练习
解:(1)0.015
8
≈0.016;(2)304.35≈304;
(3)1.804
≈1.8;
(4)1.804≈1.80.
(4)中能把1.80后面的0去掉吗?
对8四舍五入
对3四舍五入
对0四舍五入
对4四舍五入
新知应用
例3
按括号内的要求,用四舍五入法对下列各数取近似数:
(1)0.015
8(精确到0.001);
(2)304.35(精确到个位);
(3)1.804(精确到0.1);
(4)1.804(精确到0.01).
新知演练
【变式】用四舍五入法按要求取近似值:
(1)75
436(精确到百位)
(2)0.785(精确到百分位)
解:(1)75
436≈7.54×104
(2)0.785≈0.79
解:(1)600万,精确到万位;
(2)7.03万,精确到百位;
(3)5.8亿,精确到千万位;
(4)3.30×105,精确到千位.
先把数还原,再看3所在的数位.
新知应用
例4
下列由四舍五入得到的近似数,各精确到哪一位?
(1)600万;
(2)7.03万;
(3)5.8亿;
(4)3.30×105.
解:(1)精确到0.01
(2)精确到万位
(3)精确到0.00001
新知演练
【变式】下列数据精确到什么位?
(1)小王的身高1.53米;
(2)月球与地球相距38万千米;
(3)圆周率π取3.14159.
解:
从5月1日至10月31日共有184天,
故每天的平均入园人次为:
7308.44÷184≈39.719≈39.72(万人次).
新知应用
例5
据2010年上海世博会官方统计,2010年5月1日至10月31日期间,共有7308.44万人次入园参观,求每天平均入园人次(精确到0.01万人次).
拓展练习
1.生物学指出,生态系数中,每输入一个营养级的能量,大约只有10%的能量能够流动到下一个营养级,在H1→H2→H3→H4→H5→H6这条生物链中要使H6获得10千焦的能量,则需要H1提供的能量为多少?
解:10×100
000=1
000
000=106(千焦).
2.近似数1.70所表示的准确值a的范围是(
)
A.1.700<a≤1.705
B.1.60≤a<1.80
C.1.64<a≤1.705
D.1.695≤a<1.705
拓展练习
D
科学记数法:
用科学记数法表示较大的数应注意以下两点:
?1≤a<10;
?当大数是大于10的整数时,n为整数位减去1.
课堂总结
近似数:
1.判断准确数与近似数.
2.按照要求取近似数.
四舍五入到某一位,就说这个数的近似数精确到那一位.
3.由近似数判断精确度.
课堂总结
