2020年秋人教版数学八年级上册 14.2.1 平方差公式课件(共20张PPT)
文档属性
| 名称 | 2020年秋人教版数学八年级上册 14.2.1 平方差公式课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 275.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-18 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
14.2
乘法公式
14.2.1
平方差公式
葫芦岛第六初级中学
(a+b)(a?b)=
a2?b2
两个数的和与这两个数的差的积,等于这两数的平方差.这个公式叫做(乘法的)平方差公式.
1.(a
–
b
)
(
a
+
b)
=
a2
-
b2
2.(b
+
a
)(
-b
+
a
)
=
a2
-
b2
★平方差公式
★变形
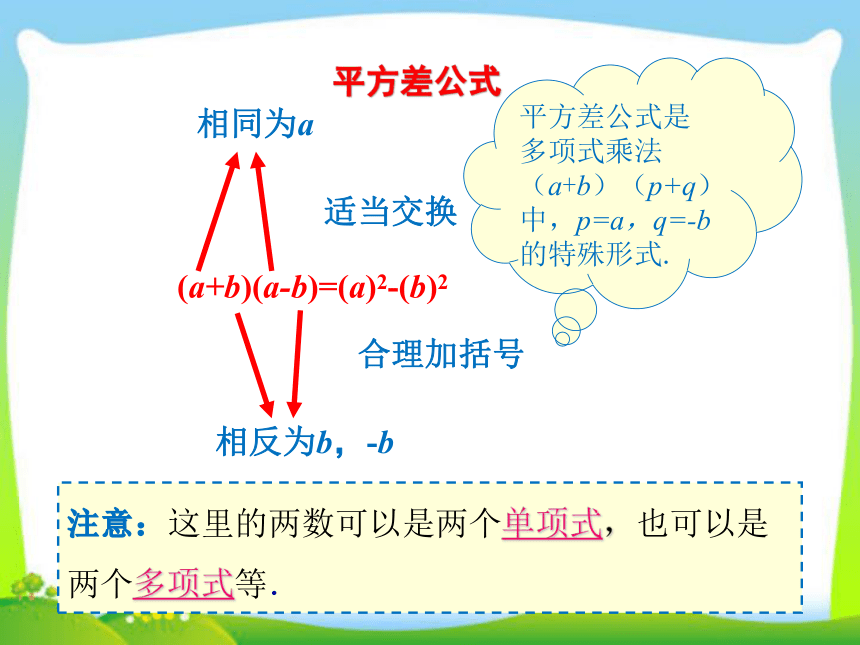
平方差公式
注意:这里的两数可以是两个单项式,也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b,-b
适当交换
合理加括号
平方差公式是
多项式乘法
(a+b)(p+q)中,p=a,q=-b的特殊形式.
填一填:
12-x2
(-3+a)(-3-a)
(a-b)(a+b)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
(1+x)(1-x)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(
0.3x)2-12
练一练:口答下列各题:
(l)(-a+b)(a+b)=_________;
(2)(a-b)(b+a)=
__________;
(3)(-a-b)(-a+b)=
________;
(4)(a-b)(-a-b)=
_________.
a2-b2
a2-b2
b2-a2
b2-a2
计算:
(1)
(3x+2
)(
3x-2
)
;
(2)(-x+2y)(-x-2y).
(2)
原式=
(-x)2
-
(2y)2
=x2
-
4y2.
解:(1)原式=(3x)2-22
=9x2-4.
解题技巧:应用平方差公式计算时,应注意以下几点:(1)左边是两个二项式相乘,并且这两个二项式中一项完全相同,另一项互为相反数;(2)右边是相同项的平方减去相反项的平方;(3)公式中的a和b可以是具体的数,也可以是单项式或多项式.
例1
【练习】利用平方差公式计算:
(1)(3x-5)(3x+5);
(2)(-2a-b)(b-2a);
(3)(-7m+8n)(-8n-7m).
解:(1)原式=(3x)2-52=9x2-25.
(2)原式=(-2a)2-b2=4a2-b2.
(3)原式=(-7m)2-(8n)2=49m2-64n2.
计算:
(1)
(y+2)
(y-2)
–
(y-1)
(y+5);
(2)
102×98
.
解:
(1)
(y+2)(y-2)-
(y-1)(y+5)
(2)102×98
=y2-4-y2-4y+5
=-
4y
+
1.
=y2-22-(y2+4y-5)
=9996.
=
(100+2)(100-2)
=
1002-22
=
10
000
–
4
通过合理变形,
利用平方差公式,可以简化运算.
不符合平方差公
式运算条件的
乘法,按乘法
法则进行运算.
例2
【练习】计算:
(1)
51×49;
(2)(3x+4)(3x-4)-(2x+3)(3x-2)
.
解:
(1)
原式=(50+1)(50-1)
=
502-12
=2500
–
1
=2499.
(2)
原式=(3x)2-42-(6x2+5x-6)
=
9x2-16-6x2-5x+6
=
3x2-5x-10.
先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-
x),其中x=1,y=2.
原式=5×12-5×22=-15.
解:原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2
=5x2-5y2.
当x=1,y=2时,
例3
对于任意的正整数n,整式(3n+1)(3n-1)-
(3-n)(3+n)的值一定是10的整数倍吗?
即(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的
倍数.
解:原式=9n2-1-(9-n2)
=10n2-10.
∵(10n2-10)÷10=n2-1,
n为正整数,
∴n2-1为整数.
解题技巧:在探究整除性或倍数问题时,一般先将代数式化为最简,然后根据结果的特征,判断其是否具有整除性或倍数关系.
例4
1.下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y)
B.(-x+y)(x-y)
C.(-x-y)(y-x)
D.(x+y)(-x-y)
C
2.计算(2x+1)(2x-1)等于( )
A.4x2-1
B.2x2-1
C.4x-1
D.4x2+1
A
3.两个正方形的边长之和为5,边长之差为2,那
么用较大的正方形的面积减去较小的正方形的
面积,差是________.
10
(1)(a+3b)(a-
3b);
=4a2-9.
=4x4-y2.
解:原式=(2a+3)(2a-3)
=a2-9b2
.
=(2a)2-32
解:原式=(-2x2
)2-y2
解:原式=a2-(3b)2
(2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y).
4.利用平方差公式计算:
5.计算:
20172
-
2016×2018.
解:
20172
-
2016×2018
=
20172
-
(2017-1)×(2017+1)
=
20172
-
(20172-12
)
=
20172
-
20172+12
=1.
6.利用平方差公式计算:
(1)(a-2)(a+2)(a2
+
4)
;
解:原式=(a2-4)(a2+4)
=a4-16.
(2)
(x-y)(x+y)(x2+y2)(x4+y4).
解:原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
7.先化简,再求值:(x+1)(x-1)+x2(1-x)+x3,
其中x=2.
解:原式=x2-1+x2-x3+x3
=2x2-1.
将x=2代入上式,
得原式=2×22-1=7.
8.已知x≠1,计算:(1+x)(1-x)=1-x2,(1-x)(1+
x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4.
(1)观察以上各式并猜想:(1-x)(1+x+x2+…+xn)=
________;(n为正整数)
(2)根据你的猜想计算:
①(1-2)(1+2+22+23+24+25)=________;
②2+22+23+…+2n=________(n为正整数);
③(x-1)(x99+x98+x97+…+x2+x+1)=________;
1-xn+1
-63
2n+1-2
x100-1
(3)通过以上规律请你进行下面的探索:
①(a-b)(a+b)=________;
②(a-b)(a2+ab+b2)=________;
③(a-b)(a3+a2b+ab2+b3)=________.
a2-b2
a3-b3
a4-b4
平方差公式
内
容
注
意
两个数的和与这两个数的差的积,等于这两个数的平方差.
字母表示:(a+b)(a-b)=a2-b2
应用时,紧紧抓住
“一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用
课堂总结
14.2
乘法公式
14.2.1
平方差公式
葫芦岛第六初级中学
(a+b)(a?b)=
a2?b2
两个数的和与这两个数的差的积,等于这两数的平方差.这个公式叫做(乘法的)平方差公式.
1.(a
–
b
)
(
a
+
b)
=
a2
-
b2
2.(b
+
a
)(
-b
+
a
)
=
a2
-
b2
★平方差公式
★变形
平方差公式
注意:这里的两数可以是两个单项式,也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b,-b
适当交换
合理加括号
平方差公式是
多项式乘法
(a+b)(p+q)中,p=a,q=-b的特殊形式.
填一填:
12-x2
(-3+a)(-3-a)
(a-b)(a+b)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
(1+x)(1-x)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(
0.3x)2-12
练一练:口答下列各题:
(l)(-a+b)(a+b)=_________;
(2)(a-b)(b+a)=
__________;
(3)(-a-b)(-a+b)=
________;
(4)(a-b)(-a-b)=
_________.
a2-b2
a2-b2
b2-a2
b2-a2
计算:
(1)
(3x+2
)(
3x-2
)
;
(2)(-x+2y)(-x-2y).
(2)
原式=
(-x)2
-
(2y)2
=x2
-
4y2.
解:(1)原式=(3x)2-22
=9x2-4.
解题技巧:应用平方差公式计算时,应注意以下几点:(1)左边是两个二项式相乘,并且这两个二项式中一项完全相同,另一项互为相反数;(2)右边是相同项的平方减去相反项的平方;(3)公式中的a和b可以是具体的数,也可以是单项式或多项式.
例1
【练习】利用平方差公式计算:
(1)(3x-5)(3x+5);
(2)(-2a-b)(b-2a);
(3)(-7m+8n)(-8n-7m).
解:(1)原式=(3x)2-52=9x2-25.
(2)原式=(-2a)2-b2=4a2-b2.
(3)原式=(-7m)2-(8n)2=49m2-64n2.
计算:
(1)
(y+2)
(y-2)
–
(y-1)
(y+5);
(2)
102×98
.
解:
(1)
(y+2)(y-2)-
(y-1)(y+5)
(2)102×98
=y2-4-y2-4y+5
=-
4y
+
1.
=y2-22-(y2+4y-5)
=9996.
=
(100+2)(100-2)
=
1002-22
=
10
000
–
4
通过合理变形,
利用平方差公式,可以简化运算.
不符合平方差公
式运算条件的
乘法,按乘法
法则进行运算.
例2
【练习】计算:
(1)
51×49;
(2)(3x+4)(3x-4)-(2x+3)(3x-2)
.
解:
(1)
原式=(50+1)(50-1)
=
502-12
=2500
–
1
=2499.
(2)
原式=(3x)2-42-(6x2+5x-6)
=
9x2-16-6x2-5x+6
=
3x2-5x-10.
先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-
x),其中x=1,y=2.
原式=5×12-5×22=-15.
解:原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2
=5x2-5y2.
当x=1,y=2时,
例3
对于任意的正整数n,整式(3n+1)(3n-1)-
(3-n)(3+n)的值一定是10的整数倍吗?
即(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的
倍数.
解:原式=9n2-1-(9-n2)
=10n2-10.
∵(10n2-10)÷10=n2-1,
n为正整数,
∴n2-1为整数.
解题技巧:在探究整除性或倍数问题时,一般先将代数式化为最简,然后根据结果的特征,判断其是否具有整除性或倍数关系.
例4
1.下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y)
B.(-x+y)(x-y)
C.(-x-y)(y-x)
D.(x+y)(-x-y)
C
2.计算(2x+1)(2x-1)等于( )
A.4x2-1
B.2x2-1
C.4x-1
D.4x2+1
A
3.两个正方形的边长之和为5,边长之差为2,那
么用较大的正方形的面积减去较小的正方形的
面积,差是________.
10
(1)(a+3b)(a-
3b);
=4a2-9.
=4x4-y2.
解:原式=(2a+3)(2a-3)
=a2-9b2
.
=(2a)2-32
解:原式=(-2x2
)2-y2
解:原式=a2-(3b)2
(2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y).
4.利用平方差公式计算:
5.计算:
20172
-
2016×2018.
解:
20172
-
2016×2018
=
20172
-
(2017-1)×(2017+1)
=
20172
-
(20172-12
)
=
20172
-
20172+12
=1.
6.利用平方差公式计算:
(1)(a-2)(a+2)(a2
+
4)
;
解:原式=(a2-4)(a2+4)
=a4-16.
(2)
(x-y)(x+y)(x2+y2)(x4+y4).
解:原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
7.先化简,再求值:(x+1)(x-1)+x2(1-x)+x3,
其中x=2.
解:原式=x2-1+x2-x3+x3
=2x2-1.
将x=2代入上式,
得原式=2×22-1=7.
8.已知x≠1,计算:(1+x)(1-x)=1-x2,(1-x)(1+
x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4.
(1)观察以上各式并猜想:(1-x)(1+x+x2+…+xn)=
________;(n为正整数)
(2)根据你的猜想计算:
①(1-2)(1+2+22+23+24+25)=________;
②2+22+23+…+2n=________(n为正整数);
③(x-1)(x99+x98+x97+…+x2+x+1)=________;
1-xn+1
-63
2n+1-2
x100-1
(3)通过以上规律请你进行下面的探索:
①(a-b)(a+b)=________;
②(a-b)(a2+ab+b2)=________;
③(a-b)(a3+a2b+ab2+b3)=________.
a2-b2
a3-b3
a4-b4
平方差公式
内
容
注
意
两个数的和与这两个数的差的积,等于这两个数的平方差.
字母表示:(a+b)(a-b)=a2-b2
应用时,紧紧抓住
“一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用
课堂总结
