5.5.2 简单的三角恒等变换(第三课时) 教案(word)
文档属性
| 名称 | 5.5.2 简单的三角恒等变换(第三课时) 教案(word) |
|
|
| 格式 | docx | ||
| 文件大小 | 67.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 00:00:00 | ||
图片预览


文档简介
《5.5.2 简单的三角恒等变换(第三课时)》
教学设计
教学目标
通过例题,回顾本节学习过的公式及常用的数学思想方法,并用于解决简单的三角变换问题,发展学生逻辑推理与数学运算素养.
教学重难点
教学重点:体会三角函数公式之间的内在联系,并运用公式解决三角恒等变换问题.
教学难点:解决一些三角恒等变换的问题.
课前准备
PPT课件.
教学过程
(一)归纳小结
问题1:两角差的余弦公式C(α-β)不仅是和(差)角公式的基础,也可以看成是诱导公式的一般化.你能画一张本章公式的“逻辑图”吗?推导这些公式的过程中用到了哪些数学思想方法?
师生活动:学生思考并回答.
预设答案:
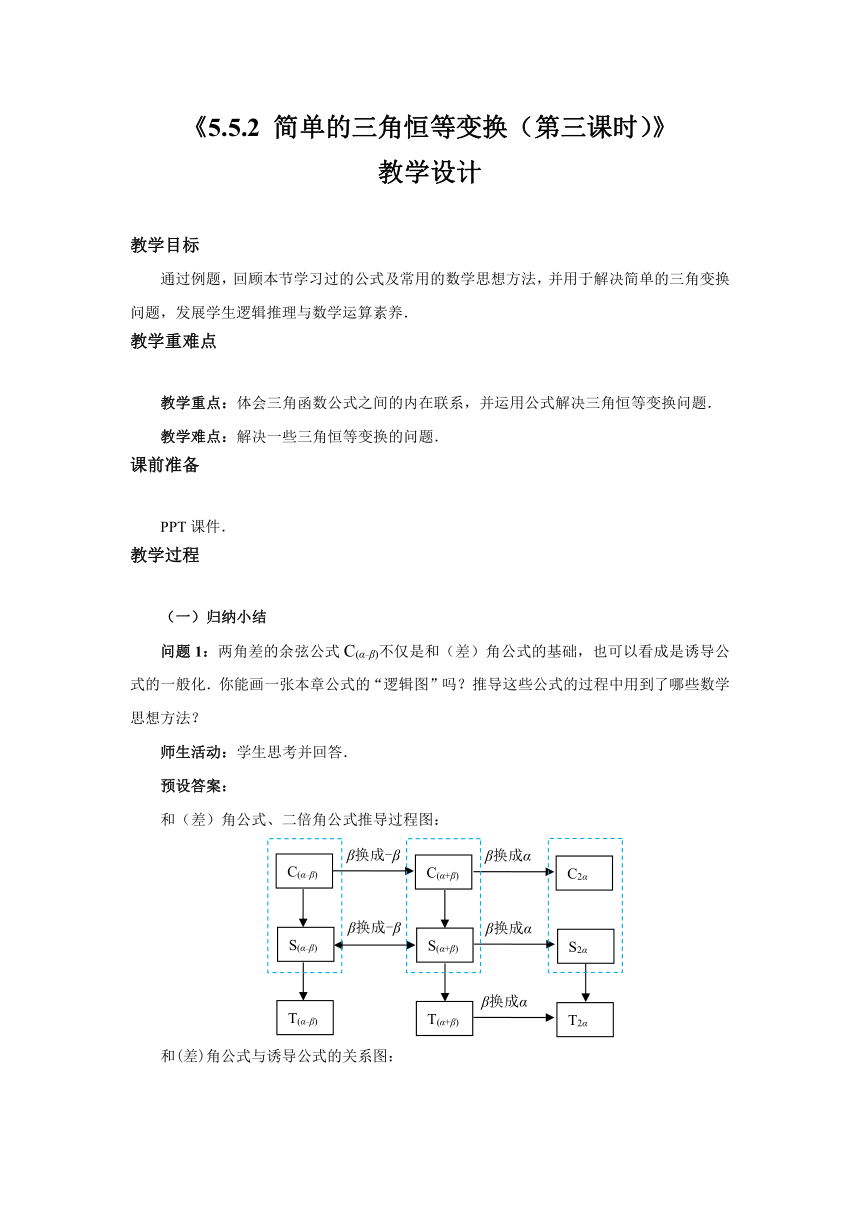
和(差)角公式、二倍角公式推导过程图:
C(α-β)
C(α+β)
C2α
β换成-β
β换成α
S(α-β)
S(α+β)
S2α
β换成-β
β换成α
T(α-β)
T(α+β)
T2α
β换成α
和(差)角公式与诱导公式的关系图:
C(α-β)
cos(2kπ+α)=cosα
-β=2kπ,k∈Z
cos(π+α)=-cosα
-β=π
cos(-β)=cosβ
α=0
cos(π-β)=-cosβ
α=π
cos(false-β)=sinβ
α=false
cos(false+α)=-sinα
-β=false
推导这些公式的过程中用到了特殊与一般、转化与化归的数学思想方法.
设计意图:回顾反思,让学生们再次感悟公式false的重要性.
例1 用false的正弦、余弦值表示false.
追问:请你观察例1中给出的问题,你能发现已知量与待求量之间的差异吗?能不能借助目前我们已经掌握的公式逐步消除或削弱这些差异?
预设的回答:变换对象中含有三个任意角,但如果把其中两个角的和或差看作一个整体,则可转化为两个角和或差的形式,可借助和角、差角公式变换求解.
设计意图:通过“差异”引导学生,鼓励他们设计变换过程,同时巩固复习本节学习的和角、差角公式并回顾推导这些公式时用到的数学思想方法,渗透整体意识、化归思想、换元法等,提升学生逻辑推理与数学运算素养.
解:false
false
false.
教师讲解:以上运算可以看出,只要掌握和角公式、差角公式,我们可以推出三个、四个甚至更多个任意角的和或差的正弦、余弦公式,它们的推导并不复杂但是形式非常复杂,因此没必要记忆它们,如果今后真的需要使用这些公式,临场推导即可.
问题2:我们运用公式进行三角恒等变换的一般思路是什么?
师生活动:学生思考并回答.
预设的答案:寻找变换对象和变换目标之间的差异(包括角度差异、名称差异、结构差异、次数差异等),并以消除或削弱差异为目的选择适当的公式进行变换.
设计意图:引导学生回顾本节核心任务,即三角恒等变换的一般思路.
例2 观察以下各等式:
sin230°+cos260°+sin 30°cos 60°=34,
sin220°+cos250°+sin 20°cos 50°=34,
sin215°+cos245°+sin 15°cos 45°=34.
分析上述各式的共同特点,写出能反映一般规律的等式,并对等式的正确性作出证明.
追问1:你打算从哪些角度分析这些式子的相同点与不同点?试逐条分析,并写出一般规律.
预设的答案:可以从角、函数名、次数三个角度着手分析.角:每个式子均包括四个角,第一、第三个角相同;第二、第四个角相同,且比第一、三个角大false;函数名:每个式子均出现四个函数名,且从左向右均为正弦、余弦、正弦、余弦;次数:各式各项均为二次.
故可归纳出等式false.
设计意图:引导学生从不同角度对比分析,进行归纳推理.
追问2:仔细观察刚才发现的规律,你能找到等式两侧的差异吗?如何设计变换方案呢?
预设的答案:有两种方案.方案一:从角度差异着手,等式左侧有false两个角,而等式右侧没有角,可将false看作两角和展开,这样可减少左侧角的个数,缩小与右侧的差异;方案二:从次数差异着手,等式左侧均为二次,右侧为非零常数,零次,故采用降幂扩角公式(半角公式),积化和差公式降低左侧次数,缩小与右侧的差异.
设计意图:引导学生发现“差异”,并设计变换过程.
解:反映一般规律的等式是false.
证法一:左边false
false
false右边.
证法二:左边false
false右边.
例3 要把半径为R的半圆形铁皮截成长方形,应怎样截取,才能使长方形面积最大?
追问1:如何将长方形的面积表示出来?
4380865104775
x
R
预设答案:如图,设出长方形的宽为x,利用长、宽、半径之间的等量关系可以表示出长false,则长方形的面积为false,然后利用函数知识求出最大值.
424561027305追问2:除了设长方形的长或宽之外,还有哪个量同样可以表示出长和宽?
预设答案:如图,可以用∠AOB表示出长和宽,从而解决面积问题.
解:如图,设圆心为O,长方形截面面积为S,∠AOB=α,则
AB=Rsinα,OB=Rcosα,
S=(Rsinα)·2(Rcosα)
=2R2sinαcosα=R2sin2α.
当sin2α取最大值,即sin2α=1时,长方形截面积最大,不难推出,α=时,长方形截面面积最大,最大截面面积等于R2.
教师讲解:解出本题的关键是找到并设出false,以往我们处理类似问题时,往往都是设边长为基本量,这是因为当时我们并没有系统地学习关于角的理论和性质.学习本章之后,我们比较系统地学习了角的概念、度量、三角函数及其图象和三角恒等变换公式等,不难发现,角是与边同等重要的几何要素.因此,今后解决几何问题时,我们应该充分关注其中的角元素.
(二)作业布置
教科书习题5.5第15,16,20题.
(三)目标检测设计
1.用false表示false.
2.已知sin θ+cos θ=2sin α,sin θ cos θ=sin2β,求证:4cos22α=cos22β.
答案:1.false.
2.由于 sin θ+cos θ=2sin α,所以(sin θ+cos θ)2=4sin2 α,
又sin θ cos θ=sin2β,因此,1+ 2sin2β =4sin2 α,2-cos2β=2-2cos2α,
故4cos22α=cos22β.
设计意图:通过若干题目,促使学生巩固本节所学公式,并能通过分析变换对象与变换目标的差异,寻找合适的切入点,设计变换过程,提升学生逻辑推理与数学运算素养.题组可为判断学生是否达到目标“借助和角、差角、倍角公式解决简单的三角恒等变换问题”提供评测依据.
教学设计
教学目标
通过例题,回顾本节学习过的公式及常用的数学思想方法,并用于解决简单的三角变换问题,发展学生逻辑推理与数学运算素养.
教学重难点
教学重点:体会三角函数公式之间的内在联系,并运用公式解决三角恒等变换问题.
教学难点:解决一些三角恒等变换的问题.
课前准备
PPT课件.
教学过程
(一)归纳小结
问题1:两角差的余弦公式C(α-β)不仅是和(差)角公式的基础,也可以看成是诱导公式的一般化.你能画一张本章公式的“逻辑图”吗?推导这些公式的过程中用到了哪些数学思想方法?
师生活动:学生思考并回答.
预设答案:
和(差)角公式、二倍角公式推导过程图:
C(α-β)
C(α+β)
C2α
β换成-β
β换成α
S(α-β)
S(α+β)
S2α
β换成-β
β换成α
T(α-β)
T(α+β)
T2α
β换成α
和(差)角公式与诱导公式的关系图:
C(α-β)
cos(2kπ+α)=cosα
-β=2kπ,k∈Z
cos(π+α)=-cosα
-β=π
cos(-β)=cosβ
α=0
cos(π-β)=-cosβ
α=π
cos(false-β)=sinβ
α=false
cos(false+α)=-sinα
-β=false
推导这些公式的过程中用到了特殊与一般、转化与化归的数学思想方法.
设计意图:回顾反思,让学生们再次感悟公式false的重要性.
例1 用false的正弦、余弦值表示false.
追问:请你观察例1中给出的问题,你能发现已知量与待求量之间的差异吗?能不能借助目前我们已经掌握的公式逐步消除或削弱这些差异?
预设的回答:变换对象中含有三个任意角,但如果把其中两个角的和或差看作一个整体,则可转化为两个角和或差的形式,可借助和角、差角公式变换求解.
设计意图:通过“差异”引导学生,鼓励他们设计变换过程,同时巩固复习本节学习的和角、差角公式并回顾推导这些公式时用到的数学思想方法,渗透整体意识、化归思想、换元法等,提升学生逻辑推理与数学运算素养.
解:false
false
false.
教师讲解:以上运算可以看出,只要掌握和角公式、差角公式,我们可以推出三个、四个甚至更多个任意角的和或差的正弦、余弦公式,它们的推导并不复杂但是形式非常复杂,因此没必要记忆它们,如果今后真的需要使用这些公式,临场推导即可.
问题2:我们运用公式进行三角恒等变换的一般思路是什么?
师生活动:学生思考并回答.
预设的答案:寻找变换对象和变换目标之间的差异(包括角度差异、名称差异、结构差异、次数差异等),并以消除或削弱差异为目的选择适当的公式进行变换.
设计意图:引导学生回顾本节核心任务,即三角恒等变换的一般思路.
例2 观察以下各等式:
sin230°+cos260°+sin 30°cos 60°=34,
sin220°+cos250°+sin 20°cos 50°=34,
sin215°+cos245°+sin 15°cos 45°=34.
分析上述各式的共同特点,写出能反映一般规律的等式,并对等式的正确性作出证明.
追问1:你打算从哪些角度分析这些式子的相同点与不同点?试逐条分析,并写出一般规律.
预设的答案:可以从角、函数名、次数三个角度着手分析.角:每个式子均包括四个角,第一、第三个角相同;第二、第四个角相同,且比第一、三个角大false;函数名:每个式子均出现四个函数名,且从左向右均为正弦、余弦、正弦、余弦;次数:各式各项均为二次.
故可归纳出等式false.
设计意图:引导学生从不同角度对比分析,进行归纳推理.
追问2:仔细观察刚才发现的规律,你能找到等式两侧的差异吗?如何设计变换方案呢?
预设的答案:有两种方案.方案一:从角度差异着手,等式左侧有false两个角,而等式右侧没有角,可将false看作两角和展开,这样可减少左侧角的个数,缩小与右侧的差异;方案二:从次数差异着手,等式左侧均为二次,右侧为非零常数,零次,故采用降幂扩角公式(半角公式),积化和差公式降低左侧次数,缩小与右侧的差异.
设计意图:引导学生发现“差异”,并设计变换过程.
解:反映一般规律的等式是false.
证法一:左边false
false
false右边.
证法二:左边false
false右边.
例3 要把半径为R的半圆形铁皮截成长方形,应怎样截取,才能使长方形面积最大?
追问1:如何将长方形的面积表示出来?
4380865104775
x
R
预设答案:如图,设出长方形的宽为x,利用长、宽、半径之间的等量关系可以表示出长false,则长方形的面积为false,然后利用函数知识求出最大值.
424561027305追问2:除了设长方形的长或宽之外,还有哪个量同样可以表示出长和宽?
预设答案:如图,可以用∠AOB表示出长和宽,从而解决面积问题.
解:如图,设圆心为O,长方形截面面积为S,∠AOB=α,则
AB=Rsinα,OB=Rcosα,
S=(Rsinα)·2(Rcosα)
=2R2sinαcosα=R2sin2α.
当sin2α取最大值,即sin2α=1时,长方形截面积最大,不难推出,α=时,长方形截面面积最大,最大截面面积等于R2.
教师讲解:解出本题的关键是找到并设出false,以往我们处理类似问题时,往往都是设边长为基本量,这是因为当时我们并没有系统地学习关于角的理论和性质.学习本章之后,我们比较系统地学习了角的概念、度量、三角函数及其图象和三角恒等变换公式等,不难发现,角是与边同等重要的几何要素.因此,今后解决几何问题时,我们应该充分关注其中的角元素.
(二)作业布置
教科书习题5.5第15,16,20题.
(三)目标检测设计
1.用false表示false.
2.已知sin θ+cos θ=2sin α,sin θ cos θ=sin2β,求证:4cos22α=cos22β.
答案:1.false.
2.由于 sin θ+cos θ=2sin α,所以(sin θ+cos θ)2=4sin2 α,
又sin θ cos θ=sin2β,因此,1+ 2sin2β =4sin2 α,2-cos2β=2-2cos2α,
故4cos22α=cos22β.
设计意图:通过若干题目,促使学生巩固本节所学公式,并能通过分析变换对象与变换目标的差异,寻找合适的切入点,设计变换过程,提升学生逻辑推理与数学运算素养.题组可为判断学生是否达到目标“借助和角、差角、倍角公式解决简单的三角恒等变换问题”提供评测依据.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
