沪科版九年级上册数学 22.2相似三角形的判定——平行线截三角形相似定理课件(共15张PPT)
文档属性
| 名称 | 沪科版九年级上册数学 22.2相似三角形的判定——平行线截三角形相似定理课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 532.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 09:19:40 | ||
图片预览


文档简介
(共15张PPT)
相似三角形判定
---预备定理(平行模型)
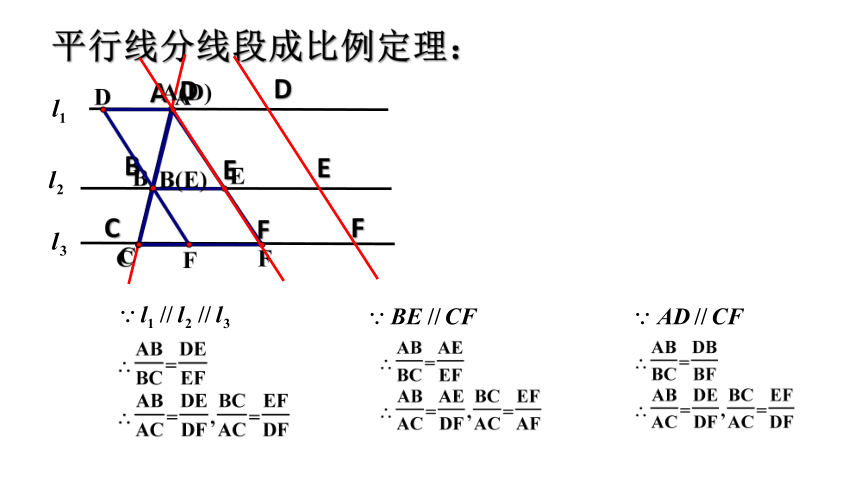
平行线分线段成比例定理:
A
C
B
F
E
D
F
E
D
一般的,两个边数相同的多边形,如果它们的对应角相等,对应边长度的比相等,那么这两个多边形叫做相似多边形。
①
②
对应角相等
对应边长度的比相等
这时,对应边长度的比叫做相似比,也叫相似系数.
相似多边形
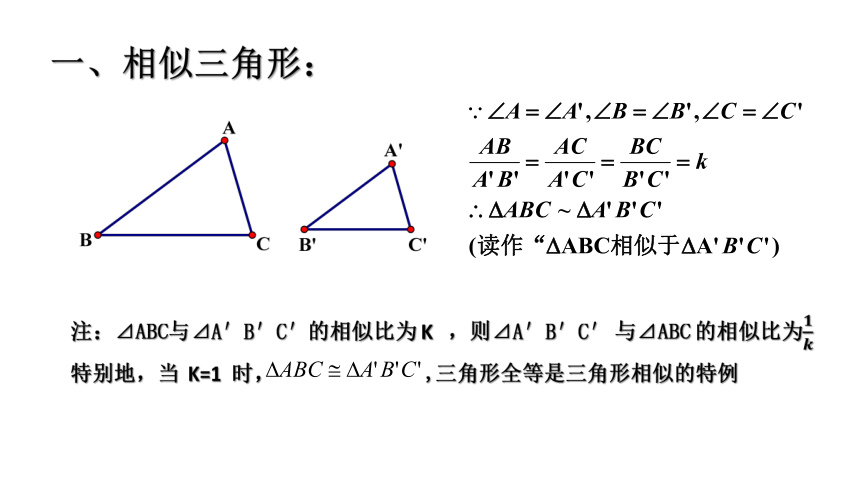
一、相似三角形:
注:⊿ABC与⊿A′B′C′的相似比为
K
,则⊿A′B′C′
与⊿ABC
的相似比为
特别地,当
K=1
时,
,三角形全等是三角形相似的特例
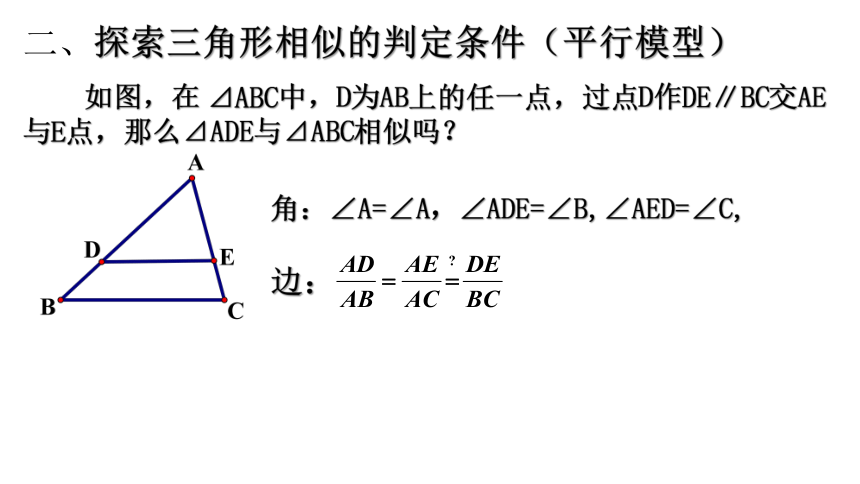
二、探索三角形相似的判定条件(平行模型)
如图,在
⊿ABC中,D为AB上的任一点,过点D作DE∥BC交AE与E点,那么⊿ADE与⊿ABC相似吗?
角:∠A=∠A,∠ADE=∠B,∠AED=∠C,
边:
二、
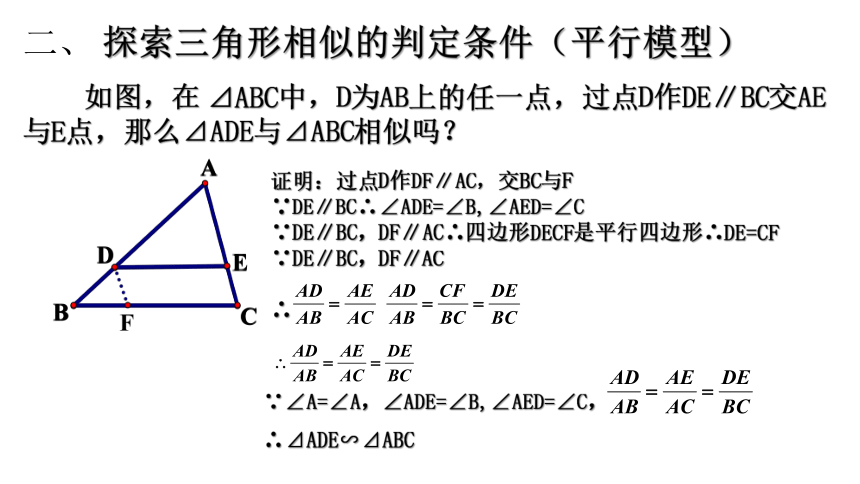
探索三角形相似的判定条件(平行模型)
如图,在
⊿ABC中,D为AB上的任一点,过点D作DE∥BC交AE与E点,那么⊿ADE与⊿ABC相似吗?
证明:过点D作DF∥AC,交BC与F
∵DE∥BC∴∠ADE=∠B,∠AED=∠C
∵DE∥BC,DF∥AC∴四边形DECF是平行四边形∴DE=CF
∵DE∥BC,DF∥AC
∴
∵∠A=∠A,∠ADE=∠B,∠AED=∠C,
∴⊿ADE∽⊿ABC
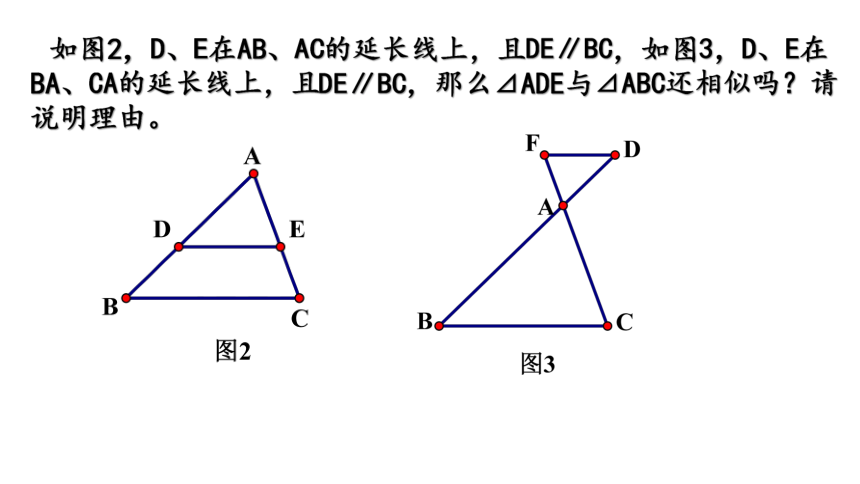
如图2,D、E在AB、AC的延长线上,且DE∥BC,如图3,D、E在BA、CA的延长线上,且DE∥BC,那么⊿ADE与⊿ABC还相似吗?请说明理由。
三角形相似的模型判定定理
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似
符号语言:∵DE∥BC
∴⊿ADE∽⊿ABC
如图,在,DE//EG//BC,写出图中的相似三角形,并求出对应的相似比。
2、已知:如图,⊿ABC中,DE∥BC,DF∥AC,则图中共有
对相似三角形
3、已知,如图,是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB的高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.
4、在平行四边形ABCD中,M、N为对角线BD的三等分点,连接AM交BC与E,连接EN并延长交AD于F
(1)试说明⊿AMD∽⊿EMB
(2)求
的值
(3)求
的值
、小结:
本节课你有什么收获?
1、三角形相似的模型判定定理
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似
符号语言:∵DE∥BC
∴⊿ADE∽⊿ABC
2、在图形中寻找平行模型
四、布置作业:
基础训练§22.2同步练习(二)
如图四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD与点E,
(1)求证:⊿CDE∽⊿FAE
(2)当E是AD的中点且BC=2CD时,求证:∠F=∠BCF
相似三角形判定
---预备定理(平行模型)
平行线分线段成比例定理:
A
C
B
F
E
D
F
E
D
一般的,两个边数相同的多边形,如果它们的对应角相等,对应边长度的比相等,那么这两个多边形叫做相似多边形。
①
②
对应角相等
对应边长度的比相等
这时,对应边长度的比叫做相似比,也叫相似系数.
相似多边形
一、相似三角形:
注:⊿ABC与⊿A′B′C′的相似比为
K
,则⊿A′B′C′
与⊿ABC
的相似比为
特别地,当
K=1
时,
,三角形全等是三角形相似的特例
二、探索三角形相似的判定条件(平行模型)
如图,在
⊿ABC中,D为AB上的任一点,过点D作DE∥BC交AE与E点,那么⊿ADE与⊿ABC相似吗?
角:∠A=∠A,∠ADE=∠B,∠AED=∠C,
边:
二、
探索三角形相似的判定条件(平行模型)
如图,在
⊿ABC中,D为AB上的任一点,过点D作DE∥BC交AE与E点,那么⊿ADE与⊿ABC相似吗?
证明:过点D作DF∥AC,交BC与F
∵DE∥BC∴∠ADE=∠B,∠AED=∠C
∵DE∥BC,DF∥AC∴四边形DECF是平行四边形∴DE=CF
∵DE∥BC,DF∥AC
∴
∵∠A=∠A,∠ADE=∠B,∠AED=∠C,
∴⊿ADE∽⊿ABC
如图2,D、E在AB、AC的延长线上,且DE∥BC,如图3,D、E在BA、CA的延长线上,且DE∥BC,那么⊿ADE与⊿ABC还相似吗?请说明理由。
三角形相似的模型判定定理
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似
符号语言:∵DE∥BC
∴⊿ADE∽⊿ABC
如图,在,DE//EG//BC,写出图中的相似三角形,并求出对应的相似比。
2、已知:如图,⊿ABC中,DE∥BC,DF∥AC,则图中共有
对相似三角形
3、已知,如图,是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB的高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.
4、在平行四边形ABCD中,M、N为对角线BD的三等分点,连接AM交BC与E,连接EN并延长交AD于F
(1)试说明⊿AMD∽⊿EMB
(2)求
的值
(3)求
的值
、小结:
本节课你有什么收获?
1、三角形相似的模型判定定理
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似
符号语言:∵DE∥BC
∴⊿ADE∽⊿ABC
2、在图形中寻找平行模型
四、布置作业:
基础训练§22.2同步练习(二)
如图四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD与点E,
(1)求证:⊿CDE∽⊿FAE
(2)当E是AD的中点且BC=2CD时,求证:∠F=∠BCF
