人教版九年级上册 数学 24.1.2垂直于弦的直径 教学设计
文档属性
| 名称 | 人教版九年级上册 数学 24.1.2垂直于弦的直径 教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 144.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览



文档简介
24.1.2垂直于弦的直径教学设计
教学目标:
1、知识与技能目标
通过观察实验,使学生理解圆的轴对称性;
掌握垂径定理,理解其证明,并会用它解决有关的证明与计算问题;
掌握辅助线的作法——连半径,作弦的垂线段。
2、过程与方法目标:通过定理探究、证明和应用的过程,发展学生的数学思维,
培养学生的观察、分析、逻辑思维和归纳概括能力。
3、情感、态度与价值观
(1)通过探究垂径定理的活动,激发学生探究、发现数学问题的兴趣,培养学生大胆猜想、乐于探究的良好品质;
(2)培养学生观察能力,激发学生的好奇心和求知欲,从数学学习活动中获得成功的体验。
二、教学重点、难点:
重点:垂径定理及其应用
难点:区分垂径定理的题设与结论
三、教具准备:圆形纸片、三角板、圆规。
四、教学过程:
教学步骤
教学内容
设计意图
一、创设情境,激疑引趣
引例:你知道赵州桥吗?它是我国隋代建造的石拱桥,
距今有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦长)为37.4m,
拱高(弧的中点到弦的距离)为7.2m,现在有个人想要知道它主桥拱的半径是多少?同学们,你能帮他求出来吗?学完了本节课的内容,我们一起来解决这个问题。
从学生熟悉的历史事物中提出问题、设置悬疑、激发学生的学习兴趣。让学生体会生活中数学随处可见,体验数学如何用来解决生活中的实际问题。
二、实验观察,得出猜想
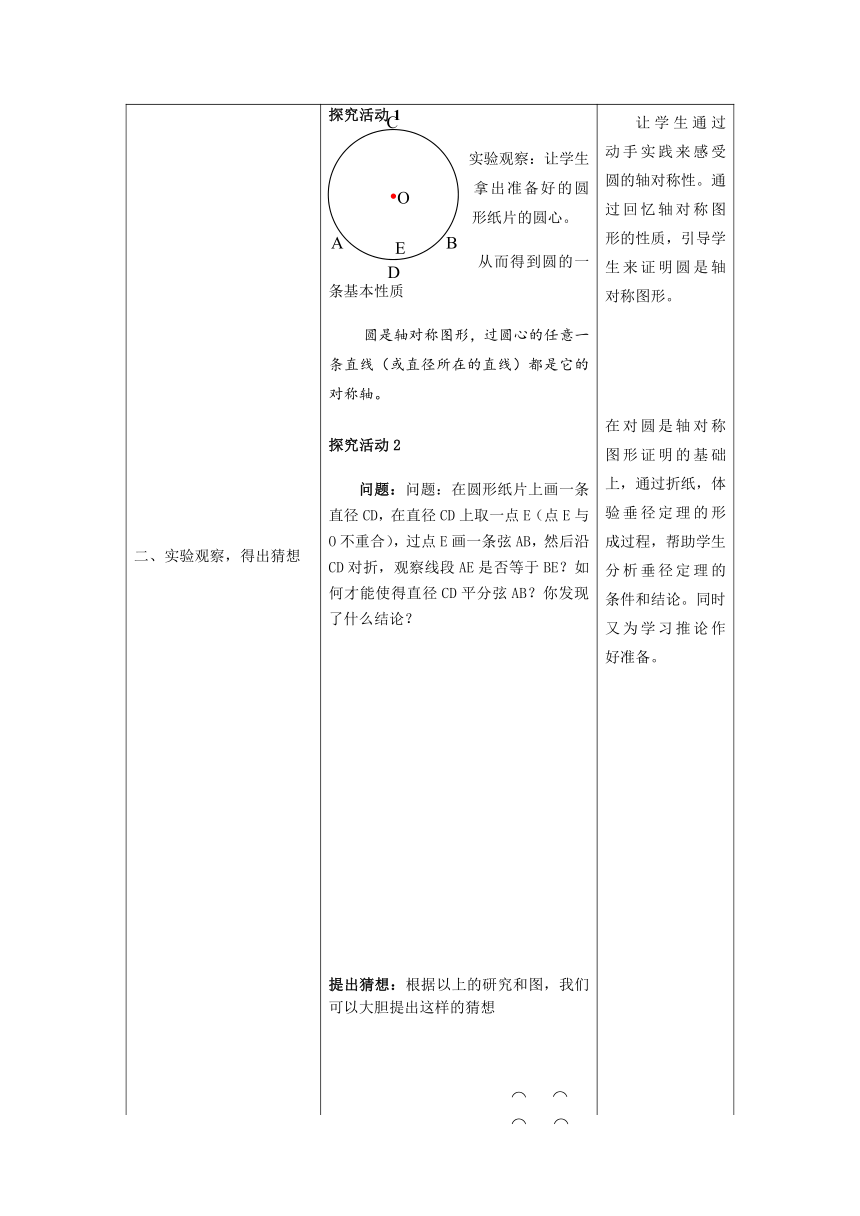
探究活动1
实验观察:让学生拿出准备好的圆形纸片的圆心。
从而得到圆的一条基本性质
圆是轴对称图形,过圆心的任意一条直线(或直径所在的直线)都是它的对称轴。
探究活动2
问题:问题:在圆形纸片上画一条直径CD,在直径CD上取一点E(点E与O不重合),过点E画一条弦AB,然后沿CD对折,观察线段AE是否等于BE?如何才能使得直径CD平分弦AB?你发现了什么结论?
(
A
B
C
D
E
O
)
提出猜想:根据以上的研究和图,我们可以大胆提出这样的猜想
(
⌒
⌒
⌒
⌒
)
(1)过圆心;(2)垂直于弦;(3)平分弦;(4)平分弦所对的优弧;(5)平分弦所对的劣弧.
验证猜想:教师用电脑课件演示图中沿直径CD对折,这条特殊直径两侧的图形能够完全重合,并给这条特殊的直径命名为——垂直于弦的直径。
让学生通过动手实践来感受圆的轴对称性。通过回忆轴对称图形的性质,引导学生来证明圆是轴对称图形。
在对圆是轴对称图形证明的基础上,通过折纸,体验垂径定理的形成过程,帮助学生分析垂径定理的条件和结论。同时又为学习推论作好准备。
三、证明猜想,归纳定理
1.证明猜想:
猜想是否正确,还有待于证明。引导学生从等腰三角形和圆的对称性两方面寻找证明思路。
2.归纳定理:
根据上面的证明,请学生自己用文字语言进行归纳,并将其命名为“垂径定理”。
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
在猜想之后对定理进行证明,这样可以加深学生对定理的理解。
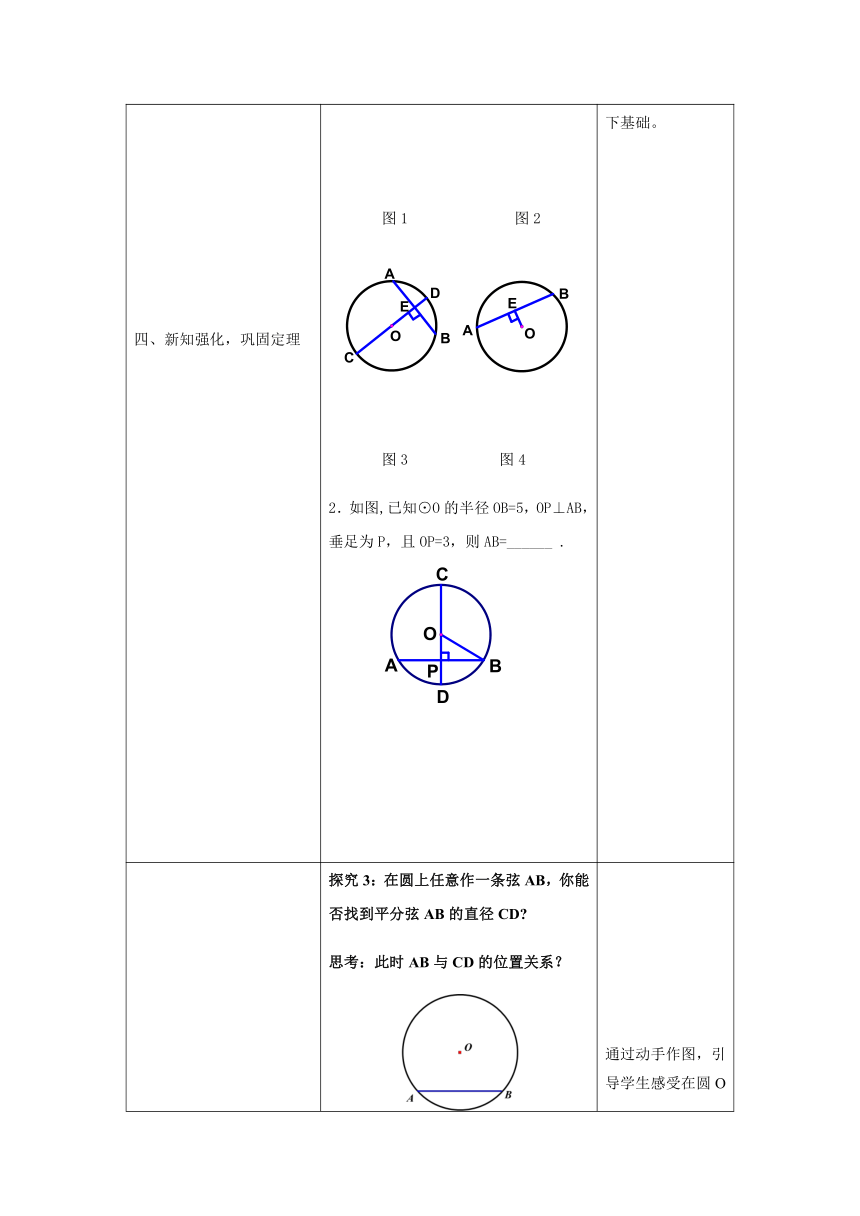
四、新知强化,巩固定理
尝试练习
1.下列图形中能否得到AE=BE,为什么?
图1
图2
图3
图4
2.如图,已知⊙O的半径OB=5,OP⊥AB,垂足为P,且OP=3,则AB=______
.
用两个简单的练习题来进一步加深学生对垂径定理的理解。对运用垂径定理来解决赵州桥的问题打下基础。
五、探究活动
探究3:在圆上任意作一条弦AB,你能否找到平分弦AB的直径CD?
思考:此时AB与CD的位置关系?
想一想:
如果弦AB是过圆心的弦呢?平分弦AB
的直径CD一定会垂直弦AB吗?
(
CD⊥AB
)思考:已知CD是直径,且平分弦AB,能否得到
,且平分弧ACB及弧AB?
猜想:
CD是圆O的直径
AE=BE
垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
通过动手作图,引导学生感受在圆O中平分弦AB的弦无数条,而满足过圆心O的弦只有一条,这一条弦就是直径。在接下来的想一想中,为了让学生对“弦AB不能是直径”的认识有深刻的印象,特意动手让学生画一画,用实践来体验为什么“弦AB不能是直径”,从而得出垂径定理的推论。
六、应用定理,解决问题
问题
:你知道赵州桥吗?它是我国隋代建造的石拱桥,
距今有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,
拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
(
AB
︵
)
(
AB
︵
)分析:如图,用
表示主桥拱,设
所在圆的圆心为O,半径为R.经过圆心O
作弦AB
的垂线OC,D为垂足,OC与AB
相交于点D,根据前面的结论,D
是AB
的中点,C是
的中点,CD
就是拱高.
方法总结:
1、作辅助线:作垂直、连半径
2、构造直角三角形
以垂径定理的图形为基本模型,根据
实际问题的条件,建立数学几何模型,来解决赵州桥问题。让学生了解到:在圆中,解决有关弦的问题是,常常需要作“垂直于弦的直径”作为辅助线。
这种添加辅助线的方法需要不断强化,让学生真正掌握。
七、同类练习
3.已知⊙O中,直径EF⊥AB于C,若CF=4,AB=16,求⊙O的半径。
习题与赵州桥问题类似,通过这道题的练习,可以加深学生对这种模型的印象。达到进一步理解和掌握垂径定理解决实际问题的目的。
八、课堂练习
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为(
).
A.4
B.6
C.8
D.10
2.已知⊙O中,若弦AB的长为8cm,圆心O到弦AB的距离(弦心距)为3cm,求⊙O的半径。
3.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。那么AC=BD吗?为什么?
方法总结:1.辅助线:作垂线、连半径。
2.找直角三角形
拓展提升:
5.
已知⊙O的直径是50
cm,⊙O的两
条平行弦AB=40
cm
,CD=48cm,请算一
算弦AB与CD之间的距离。
课堂练习的设置由易到难,以不同的形式来强化学生对垂径定理的认识。从练习中归纳总结解题的方法,从而使学生掌握此类问题的解题方法和技巧。
九、课堂小结
1.定理的三种基本图形:如图1、2、3
2.计算中三个量的关系:
如图4:
。
。
3.证明中常用的辅助线——作弦心距。
(图1)
(图2)
(图3)
(图4)
总结方法,进一步加深学生运用垂径定理解决问题方法的印象。在今后运用垂径定理解决问题中做到心中有数。
教学目标:
1、知识与技能目标
通过观察实验,使学生理解圆的轴对称性;
掌握垂径定理,理解其证明,并会用它解决有关的证明与计算问题;
掌握辅助线的作法——连半径,作弦的垂线段。
2、过程与方法目标:通过定理探究、证明和应用的过程,发展学生的数学思维,
培养学生的观察、分析、逻辑思维和归纳概括能力。
3、情感、态度与价值观
(1)通过探究垂径定理的活动,激发学生探究、发现数学问题的兴趣,培养学生大胆猜想、乐于探究的良好品质;
(2)培养学生观察能力,激发学生的好奇心和求知欲,从数学学习活动中获得成功的体验。
二、教学重点、难点:
重点:垂径定理及其应用
难点:区分垂径定理的题设与结论
三、教具准备:圆形纸片、三角板、圆规。
四、教学过程:
教学步骤
教学内容
设计意图
一、创设情境,激疑引趣
引例:你知道赵州桥吗?它是我国隋代建造的石拱桥,
距今有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦长)为37.4m,
拱高(弧的中点到弦的距离)为7.2m,现在有个人想要知道它主桥拱的半径是多少?同学们,你能帮他求出来吗?学完了本节课的内容,我们一起来解决这个问题。
从学生熟悉的历史事物中提出问题、设置悬疑、激发学生的学习兴趣。让学生体会生活中数学随处可见,体验数学如何用来解决生活中的实际问题。
二、实验观察,得出猜想
探究活动1
实验观察:让学生拿出准备好的圆形纸片的圆心。
从而得到圆的一条基本性质
圆是轴对称图形,过圆心的任意一条直线(或直径所在的直线)都是它的对称轴。
探究活动2
问题:问题:在圆形纸片上画一条直径CD,在直径CD上取一点E(点E与O不重合),过点E画一条弦AB,然后沿CD对折,观察线段AE是否等于BE?如何才能使得直径CD平分弦AB?你发现了什么结论?
(
A
B
C
D
E
O
)
提出猜想:根据以上的研究和图,我们可以大胆提出这样的猜想
(
⌒
⌒
⌒
⌒
)
(1)过圆心;(2)垂直于弦;(3)平分弦;(4)平分弦所对的优弧;(5)平分弦所对的劣弧.
验证猜想:教师用电脑课件演示图中沿直径CD对折,这条特殊直径两侧的图形能够完全重合,并给这条特殊的直径命名为——垂直于弦的直径。
让学生通过动手实践来感受圆的轴对称性。通过回忆轴对称图形的性质,引导学生来证明圆是轴对称图形。
在对圆是轴对称图形证明的基础上,通过折纸,体验垂径定理的形成过程,帮助学生分析垂径定理的条件和结论。同时又为学习推论作好准备。
三、证明猜想,归纳定理
1.证明猜想:
猜想是否正确,还有待于证明。引导学生从等腰三角形和圆的对称性两方面寻找证明思路。
2.归纳定理:
根据上面的证明,请学生自己用文字语言进行归纳,并将其命名为“垂径定理”。
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
在猜想之后对定理进行证明,这样可以加深学生对定理的理解。
四、新知强化,巩固定理
尝试练习
1.下列图形中能否得到AE=BE,为什么?
图1
图2
图3
图4
2.如图,已知⊙O的半径OB=5,OP⊥AB,垂足为P,且OP=3,则AB=______
.
用两个简单的练习题来进一步加深学生对垂径定理的理解。对运用垂径定理来解决赵州桥的问题打下基础。
五、探究活动
探究3:在圆上任意作一条弦AB,你能否找到平分弦AB的直径CD?
思考:此时AB与CD的位置关系?
想一想:
如果弦AB是过圆心的弦呢?平分弦AB
的直径CD一定会垂直弦AB吗?
(
CD⊥AB
)思考:已知CD是直径,且平分弦AB,能否得到
,且平分弧ACB及弧AB?
猜想:
CD是圆O的直径
AE=BE
垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
通过动手作图,引导学生感受在圆O中平分弦AB的弦无数条,而满足过圆心O的弦只有一条,这一条弦就是直径。在接下来的想一想中,为了让学生对“弦AB不能是直径”的认识有深刻的印象,特意动手让学生画一画,用实践来体验为什么“弦AB不能是直径”,从而得出垂径定理的推论。
六、应用定理,解决问题
问题
:你知道赵州桥吗?它是我国隋代建造的石拱桥,
距今有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,
拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
(
AB
︵
)
(
AB
︵
)分析:如图,用
表示主桥拱,设
所在圆的圆心为O,半径为R.经过圆心O
作弦AB
的垂线OC,D为垂足,OC与AB
相交于点D,根据前面的结论,D
是AB
的中点,C是
的中点,CD
就是拱高.
方法总结:
1、作辅助线:作垂直、连半径
2、构造直角三角形
以垂径定理的图形为基本模型,根据
实际问题的条件,建立数学几何模型,来解决赵州桥问题。让学生了解到:在圆中,解决有关弦的问题是,常常需要作“垂直于弦的直径”作为辅助线。
这种添加辅助线的方法需要不断强化,让学生真正掌握。
七、同类练习
3.已知⊙O中,直径EF⊥AB于C,若CF=4,AB=16,求⊙O的半径。
习题与赵州桥问题类似,通过这道题的练习,可以加深学生对这种模型的印象。达到进一步理解和掌握垂径定理解决实际问题的目的。
八、课堂练习
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为(
).
A.4
B.6
C.8
D.10
2.已知⊙O中,若弦AB的长为8cm,圆心O到弦AB的距离(弦心距)为3cm,求⊙O的半径。
3.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。那么AC=BD吗?为什么?
方法总结:1.辅助线:作垂线、连半径。
2.找直角三角形
拓展提升:
5.
已知⊙O的直径是50
cm,⊙O的两
条平行弦AB=40
cm
,CD=48cm,请算一
算弦AB与CD之间的距离。
课堂练习的设置由易到难,以不同的形式来强化学生对垂径定理的认识。从练习中归纳总结解题的方法,从而使学生掌握此类问题的解题方法和技巧。
九、课堂小结
1.定理的三种基本图形:如图1、2、3
2.计算中三个量的关系:
如图4:
。
。
3.证明中常用的辅助线——作弦心距。
(图1)
(图2)
(图3)
(图4)
总结方法,进一步加深学生运用垂径定理解决问题方法的印象。在今后运用垂径定理解决问题中做到心中有数。
同课章节目录
