人教版数学九年级上课件:第二十二章二次函数复习课(21张)
文档属性
| 名称 | 人教版数学九年级上课件:第二十二章二次函数复习课(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 419.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 00:00:00 | ||
图片预览








文档简介
二次函数
复习课
诗人眼里的二次函数:
数学家眼里的二次函数:
同学们眼里的二次函数:
难
数 ,图象
优美而舒张的抛物线,犹如人生的轨迹,年少时的努力攀升,力争到达人生的巅峰,但岁月无情的流逝,转而向下
本节复习重难点
1.二次函数的概念
2.二次函数的图象与性质
3. a 、b、c、△符号的确定
4.待定系数法求二次函数解析式
5.抛物线旳平移
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。
定义要点:①a ≠ 0 ②最高次数为2
③代数式一定是整式
2.函数 ,当 m= 时,它是二次函数
1.二次函数的概念
练习:1、y=-x?,y=2x?-2/x,y=100-5 x?,
y=3 x?-2x?+5,其中是二次函数的有____个
2.二次函数的图象和性质
y
x
o
o
y
x
图象与性质
开口方向
顶点
对称轴
增减性
最值
二次函数的图象是____________.
抛物线
a
b
c
2a+b
2a-b
b2-4ac
a+b+c
a-b+c
4a+2b+c
4a-2b+c
开口方向 向上a>0 向下a对称轴与y轴比较 左侧ab同号 右侧ab异号
与y轴交点 交于正半轴c>o 负半轴c<0
- 与1比较
- 与-1比较
与x轴交点个数
令x=1,看纵坐标
令x=-1,看纵坐标
令x=2,看纵坐标
令x=-2,看纵坐标
3.a 、b、c、△符号的确定
典型例题1.
如图,是抛物线y=ax2+bx+c的图象,则①a 0;②b 0;?c 0;?a+b+c 0;
?a-b+c 0;?b2-4ac 0;?2a-b 0;
<
<
>
<
>
>
=
由形定数
典型例题2.
已知a<0,b>0,c>0,那么抛物线y=ax2+bx+c的顶点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
A
由数定形
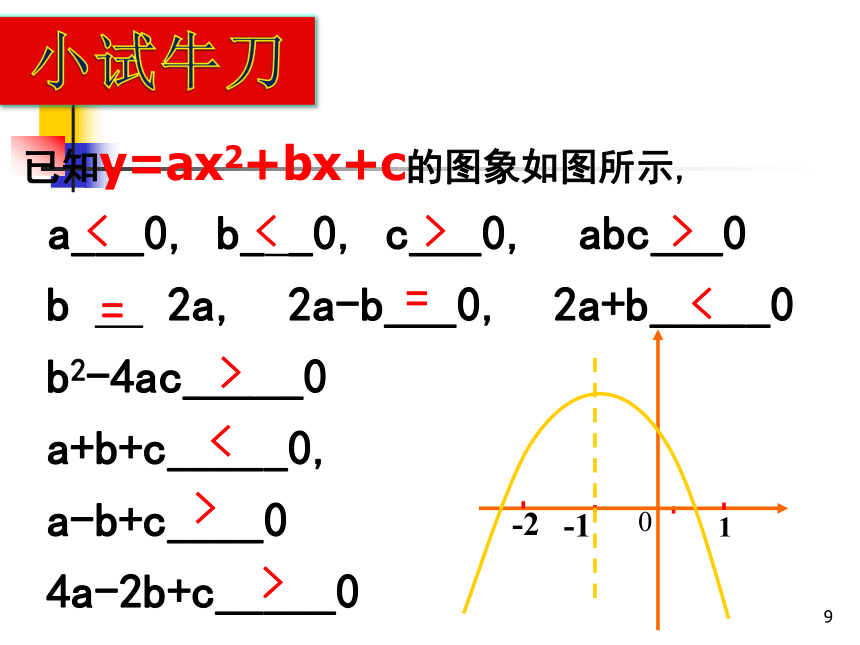
已知y=ax2+bx+c的图象如图所示,
a___0, b_ _0, c___0, abc___0
b 2a, 2a-b___0, 2a+b_____0
b2-4ac_____0
a+b+c_____0,
a-b+c____0
4a-2b+c_____0
<
<
>
>
=
=
<
>
<
>
>
0
-1
1
-2
小试牛刀
2,顶点式:已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________
求出表达式后化为一般形式.
3,交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________
求出表达式后化为一般形式.
1、一般式:已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2) (a≠0)
四.待定系数法求二次函数解析式
根据下列条件,求二次函数的解析式。
(1)、图象经过(0,0), (1,-2) , (2,3) 三点;
(2)、图象的顶点(2,3), 且经过点(3,1) ;
小试牛刀
已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。
解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x
乘胜追击
5、抛物线的平移
上加下减,左加右减
练习
⑴二次函数y=2x2的图象向 平移 个单位可得到y=2x2-3的图象;
二次函数y=2x2的图象向 平移 个单位可得到y=2(x-3)2的图象。
⑵二次函数y=2x2的图象先向 平移 个单位,再向 平移 个单位可得到函数y=2(x+1)2+2的图象。
下
3
右
3
左
1
上
2
引申:y=2(x+3)2-4 y=2(x+1)2+2
由二次函数y=x2的图象经过如何平移可以得到函数y=x2-5x+6的图象.
y=x2-5x+6
y=x2
乘胜追击
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,A,B的坐标。
(3)x为何值时,y随的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
已知二次函数
综合运用
0
?
(-1,-2)
?
?
(0,-–)
?
?
(-3,0)
(1,0)
3
2
y
x
由图象可知:
当x< -3或x>1时,y > 0
当-3 < x < 1时,y < 0
(4)
方法归纳
本节课重要的数学思想方法 : 数形结合法
函数的解析式为载体,
图象为核心
谈收获……
1.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图像大致为 ( )
B
2.二次函数y=x2+bx+c
的图像如图所示,则函数值
y<0时,对应的x取值范围
是 .
-3<x<1
-3
-3
1
当堂检测:
3、已知二次函数y=ax2+bx+c的
图像如图所示,下列结论:
① a+b+c<0,②a-b+c>0;
③ abc>0;④b=2a
中正确个数为 ( )
A.4个 B.3个
C.2个 D.1个
A
当x= 1时,y=a+b+c
当x=-1时,y=a-b+c
a <0,b <0,c>0
x=
=-1
D
4、若抛物线y=ax2+3x+1与x轴有两
个交点,则a的取值范围是 ( )
A.a>0 B.a>
C.a> D.a< 且a≠0
5、二次函数y=x2+1的图象的顶点坐标是 .
6、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .
7、二次函数y=x2-2x+2 当x= 时,y的最小为 值 .
生活是数学的源泉,探索是数学的生命线.
复习课
诗人眼里的二次函数:
数学家眼里的二次函数:
同学们眼里的二次函数:
难
数 ,图象
优美而舒张的抛物线,犹如人生的轨迹,年少时的努力攀升,力争到达人生的巅峰,但岁月无情的流逝,转而向下
本节复习重难点
1.二次函数的概念
2.二次函数的图象与性质
3. a 、b、c、△符号的确定
4.待定系数法求二次函数解析式
5.抛物线旳平移
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。
定义要点:①a ≠ 0 ②最高次数为2
③代数式一定是整式
2.函数 ,当 m= 时,它是二次函数
1.二次函数的概念
练习:1、y=-x?,y=2x?-2/x,y=100-5 x?,
y=3 x?-2x?+5,其中是二次函数的有____个
2.二次函数的图象和性质
y
x
o
o
y
x
图象与性质
开口方向
顶点
对称轴
增减性
最值
二次函数的图象是____________.
抛物线
a
b
c
2a+b
2a-b
b2-4ac
a+b+c
a-b+c
4a+2b+c
4a-2b+c
开口方向 向上a>0 向下a
与y轴交点 交于正半轴c>o 负半轴c<0
- 与1比较
- 与-1比较
与x轴交点个数
令x=1,看纵坐标
令x=-1,看纵坐标
令x=2,看纵坐标
令x=-2,看纵坐标
3.a 、b、c、△符号的确定
典型例题1.
如图,是抛物线y=ax2+bx+c的图象,则①a 0;②b 0;?c 0;?a+b+c 0;
?a-b+c 0;?b2-4ac 0;?2a-b 0;
<
<
>
<
>
>
=
由形定数
典型例题2.
已知a<0,b>0,c>0,那么抛物线y=ax2+bx+c的顶点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
A
由数定形
已知y=ax2+bx+c的图象如图所示,
a___0, b_ _0, c___0, abc___0
b 2a, 2a-b___0, 2a+b_____0
b2-4ac_____0
a+b+c_____0,
a-b+c____0
4a-2b+c_____0
<
<
>
>
=
=
<
>
<
>
>
0
-1
1
-2
小试牛刀
2,顶点式:已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________
求出表达式后化为一般形式.
3,交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________
求出表达式后化为一般形式.
1、一般式:已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2) (a≠0)
四.待定系数法求二次函数解析式
根据下列条件,求二次函数的解析式。
(1)、图象经过(0,0), (1,-2) , (2,3) 三点;
(2)、图象的顶点(2,3), 且经过点(3,1) ;
小试牛刀
已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。
解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x
乘胜追击
5、抛物线的平移
上加下减,左加右减
练习
⑴二次函数y=2x2的图象向 平移 个单位可得到y=2x2-3的图象;
二次函数y=2x2的图象向 平移 个单位可得到y=2(x-3)2的图象。
⑵二次函数y=2x2的图象先向 平移 个单位,再向 平移 个单位可得到函数y=2(x+1)2+2的图象。
下
3
右
3
左
1
上
2
引申:y=2(x+3)2-4 y=2(x+1)2+2
由二次函数y=x2的图象经过如何平移可以得到函数y=x2-5x+6的图象.
y=x2-5x+6
y=x2
乘胜追击
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,A,B的坐标。
(3)x为何值时,y随的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
已知二次函数
综合运用
0
?
(-1,-2)
?
?
(0,-–)
?
?
(-3,0)
(1,0)
3
2
y
x
由图象可知:
当x< -3或x>1时,y > 0
当-3 < x < 1时,y < 0
(4)
方法归纳
本节课重要的数学思想方法 : 数形结合法
函数的解析式为载体,
图象为核心
谈收获……
1.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图像大致为 ( )
B
2.二次函数y=x2+bx+c
的图像如图所示,则函数值
y<0时,对应的x取值范围
是 .
-3<x<1
-3
-3
1
当堂检测:
3、已知二次函数y=ax2+bx+c的
图像如图所示,下列结论:
① a+b+c<0,②a-b+c>0;
③ abc>0;④b=2a
中正确个数为 ( )
A.4个 B.3个
C.2个 D.1个
A
当x= 1时,y=a+b+c
当x=-1时,y=a-b+c
a <0,b <0,c>0
x=
=-1
D
4、若抛物线y=ax2+3x+1与x轴有两
个交点,则a的取值范围是 ( )
A.a>0 B.a>
C.a> D.a< 且a≠0
5、二次函数y=x2+1的图象的顶点坐标是 .
6、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .
7、二次函数y=x2-2x+2 当x= 时,y的最小为 值 .
生活是数学的源泉,探索是数学的生命线.
同课章节目录
