北师大七年级数学下册第四章三角形单元教案
文档属性
| 名称 | 北师大七年级数学下册第四章三角形单元教案 |  | |
| 格式 | zip | ||
| 文件大小 | 304.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 19:36:37 | ||
图片预览




文档简介
第四章
三角形
4.1 认识三角形
第1课时 三角形的定义和内角和
1.理解并掌握三角形的概念,会用符号表示三角形.
2.通过剪拼、平移等操作,掌握三角形内角和定理,并能利用三角形内角和定理解决简单问题.
3.能根据三角形内角的大小将三角形分类,并掌握直角三角形的相关性质.
自学指导 阅读教材P81~83,完成下列问题.
(一)知识探究
1.三角形
(1)定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
(2)有关概念:
如图,线段AB,BC,AC是三角形的边,点A,B,C是三角形的顶点,∠A,∠B,∠C是相邻两边组成的角,叫做三角形的内角,简称三角形的角.
(3)表示方法:顶点是A,B,C的三角形,记作“△ABC”,读作“三角形ABC”.
2.三角形三个内角的和等于180°.
3.三角形按角分类:
(1)锐角三角形:三个内角都是锐角;
(2)直角三角形:有一个内角是直角;
(3)钝角三角形:有一个内角是钝角.
4.直角三角形:
如图,我们用符号“Rt△ABC”表示“直角三角形ABC”.把直角所对的边称为直角三角形的斜边,夹直角的两条边称为直角边.直角三角形的两个锐角互余.
(二)自学反馈
1.三角形是(
B
)
A.连接任意三点组成的图形
B.由不在同一直线上的三条线段首尾顺次相接所组成的图形
C.由三条线段组成的图形
D.以上说法均不对
2.如图,△ABC中,∠A=60°,∠B=40°,则∠C等于(
B
)
A.100°
B.80°
C.60°
D.40°
活动1 小组讨论
例1 在△ABC中,∠A的度数是∠B的度数的3倍,∠C比∠B大15°,求∠A,∠B,∠C的度数.
解:设∠B为x°,则∠A为(3x)°,∠C为(x+15)°,从而有
3x+x+(x+15)=180.
解得x=33.
所以3x=99,x+15=48.
答:∠A,∠B,∠C的度数分别为99°,33°,48°.
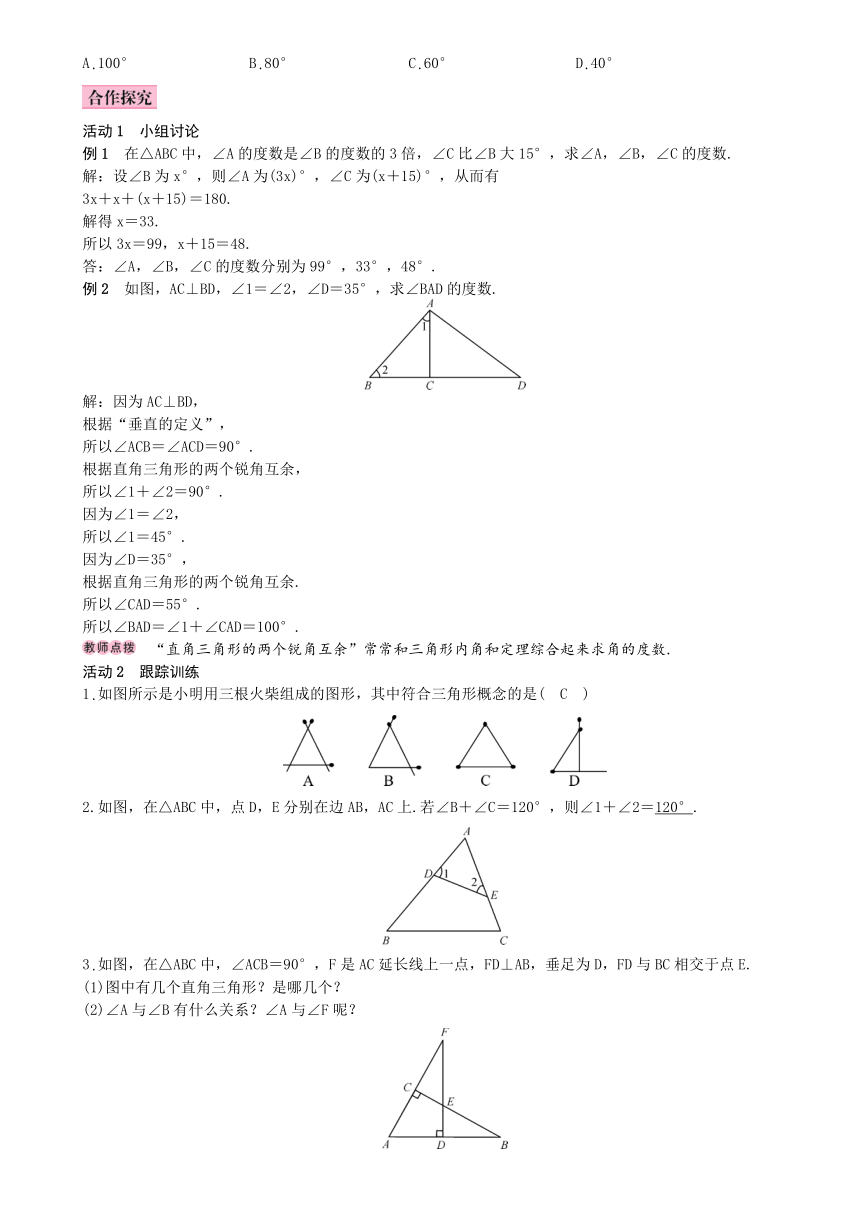
例2 如图,AC⊥BD,∠1=∠2,∠D=35°,求∠BAD的度数.
解:因为AC⊥BD,
根据“垂直的定义”,
所以∠ACB=∠ACD=90°.
根据直角三角形的两个锐角互余,
所以∠1+∠2=90°.
因为∠1=∠2,
所以∠1=45°.
因为∠D=35°,
根据直角三角形的两个锐角互余.
所以∠CAD=55°.
所以∠BAD=∠1+∠CAD=100°.
“直角三角形的两个锐角互余”常常和三角形内角和定理综合起来求角的度数.
活动2 跟踪训练
1.如图所示是小明用三根火柴组成的图形,其中符合三角形概念的是(
C
)
2.如图,在△ABC中,点D,E分别在边AB,AC上.若∠B+∠C=120°,则∠1+∠2=120°.
3.如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E.
(1)图中有几个直角三角形?是哪几个?
(2)∠A与∠B有什么关系?∠A与∠F呢?
解:(1)4个,分别是△ABC,△CEF,△ADF,△BDE.
(2)∠A+∠B=90°,∠A+∠F=90°.
活动3 课堂小结
本节课我们主要学习了三角形的内角和、三角形按角分类、直角三角形的性质,以及相关的运用.
第2课时 三角形的三边关系
1.会按边对三角形进行分类.
2.通过度量三角形的边长,理解并掌握三角形的三边关系.
自学指导 阅读教材P85~86“随堂练习”之前的内容,完成下列问题.
(一)知识探究
1.三角形按边分类如下:
三角形
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
2.三角形任意两边之和大于第三边,任意两边之差小于第三边.
(二)自学反馈
1.下列说法正确的有(
B
)
①等边三角形是等腰三角形;②三角形的两边之差大于第三边;③三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
A.1个
B.2个
C.3个
D.4个
2.下列长度的三条线段能否组成三角形?为什么?
(1)3,4,8;
解:不能组成三角形,因为3和4的和小于8.
(2)2,5,6;
解:能组成三角形,因为2和5的和大于6,且任意两边的差小于第三边.
(3)5,6,10;
解:能组成三角形,因为5和6的和大于10,且任意两边的差小于第三边.
(4)5,6,11.
解:不能组成三角形,因为5和6的和等于11.
用较短的两条线段之和与最长的线段比较,若和大,则能组成三角形,反之,则不能.
活动1 小组讨论
例1 若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
解:设第三边的长为x,
根据两边之和大于第三边,得x<2+7,即x<9.
根据两边之差小于第三边,得x>7-2,即x>5.
所以x的值大于5小于9.
又因为它是奇数,
所以x只能取7.
例2 用一根长为18厘米的细铁丝围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4厘米的等腰三角形吗?
解:(1)设底边长为x厘米,则腰长为2x厘米.
x+2x+2x=18.
解得x=3.6.
所以三边长分别为3.6厘米,7.2厘米,7.2厘米.
(2)①当4厘米长为底边,设腰长为x厘米,则
4+2x=18.
解得x=7.
所以可围成三边长分别为7厘米、7厘米、4厘米的等腰三角形.
②当4厘米长为腰长,设底边长为x厘米,则
4×2+x=18.解得x=10.
因为4+4<10,
所以此时不能构成三角形.
在不明确给出的边是等腰三角形的腰还是底边时,要分情况进行讨论,同时还要考虑到求出的各边长度能否构成三角形.
活动2 跟踪训练
1.已知△ABC三边a,b,c满足(a-b)2+=0,则△ABC的形状是(
C
)
A.钝角三角形
B.直角三角形
C.等边三角形
D.以上都不对
2.一个等腰三角形的周长为18
cm,一边长为7
cm,求其他两边的长.
解:①若7
cm为腰长,则另一腰长为7
cm,底边长为18-7-7=4(cm),且7
cm,7
cm,4
cm能围成三角形;
②若7
cm为底边长,则腰长为(18-7)÷2=5.5(cm),且7
cm,5.5
cm,5.5
cm也能围成三角形.
故其他两边长分别为7
cm,4
cm或5.5
cm,5.5
cm.
活动3 课堂小结
这节课我们主要学习了:(1)三角形按边分类;(2)三角形的三边关系.第3课时 三角形的中线、角平分线
1.认识三角形的中线、重心、角平分线.
2.能准确画出三角形的中线、角平分线.
自学指导 阅读教材P87~88,完成下列问题.
(一)知识探究
1.在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线.一个三角形共有三条中线,它们都在三角形内部,且交于一点,这点称为三角形的重心.
2.在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.简称三角形的角平分线.一个三角形共有三条角平分线,且交于一点.
(二)自学反馈
1.一个钝角三角形的三条角平分线所在的直线交于一点,这个交点一定在(
A
)
A.三角形内部
B.三角形的一边上
C.三角形外部
D.三角形的某个顶点上
2.填空:
(1)AD是△ABC的角平分线(D在BC所在直线上),那么∠BAD=∠CAD=∠BAC;
(2)AE是△ABC的中线(E在BC所在直线上),那么BE=EC=BC.
活动1 小组讨论
例1 如图,已知△ABC的周长为21
cm,AB=6
cm,BC边上的中线AD=5
cm,△ABD的周长为15
cm,求AC的长.
解:因为AB=6
cm,AD=5
cm,△ABD的周长为15
cm,
所以BD=15-6-5=4(cm).
因为AD是BC边上的中线,
所以BC=8
cm.
因为△ABC的周长为21
cm,
所以AC=21-6-8=7(cm).
例2 如图,在△ABC中,已知∠ABC=80°,∠ACB=40°,BO,CO平分∠ABC,∠ACB,求∠BOC的度数.
解:因为在△ABC中,∠ABC=80°,∠ACB=40°,BO,CO分别平分∠ABC,∠ACB,
所以∠OBC=∠ABC=×80°=40°,∠OCB=∠ACB=×40°=20°.
所以∠BOC=180°-∠OBC-∠OCB=120°.
活动2 跟踪训练
1.如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是(
D
)
A.△DEC中∠C的对边是DE
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.DE是△ABC的中线
2.如图,△ABC中,∠B=90°,AD平分∠BAC,且∠C=4∠BAD,求∠ADC的度数.
解:因为∠B=90°,
所以∠BAC+∠C=90°.
因为AD平分∠BAC,
所以∠BAD=∠CAD.
因为∠C=4∠BAD,
所以2∠BAD+4∠BAD=90°.
所以∠BAD=∠CAD=15°.
所以∠ADC=180°-∠CAD-∠C=180°-15°-60°=105°.
活动3 课堂小结
通过本节课的学习,我们认识三角形的角平分线、中线,并知道了三角形的三条角平分线的交点、三条中线的交点的位置.
第4课时 三角形的高线
1.认识三角形的高线,能画任意三角形的高.
2.了解三角形三条高所在直线交于一点的性质.
自学指导 阅读教材P89~90,完成下列问题.
(一)知识探究
(1)三角形的高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
(2)锐角三角形的三条高在三角形的内部;直角三角形的三条高交于直角顶点处;钝角三角形的三条高所在直线交于一点,此点在三角形的外部.
(二)自学反馈
1.如图,过△ABC的顶点A作BC边上的高,以下作法正确的是(
A
)
回忆并演示“过一点画已知直线的垂线”画法.
2.不一定在三角形内部的是(
C
)
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
活动1 小组讨论
例 如图,在△ABC中,∠BAC=80°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高.
解:(1)因为∠BAC=80°,AE是∠BAC的平分线,
所以∠CAE=40°.
因为AD⊥BC,∠C=60°,
所以∠CAD=30°.
所以∠DAE=10°.
(2)△ABC,△ABE,△AED,△ACD,△ACE,△ABD.
活动2 跟踪训练
1.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是(
C
)
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
2.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
解:(1)因为∠ACB=90°,
所以∠A+∠B=90°.
因为∠1=∠B,
所以∠A+∠1=90°.
所以∠ADC=90°.
所以CD是△ABC的高.
(2)因为∠ACB=90°,AC=8,BC=6,
所以△ABC的面积为24.
因为AB=10,CD是高,
所以CD=4.8.
活动3 课堂小结
通过本节课的学习,我们认识了三角形的高,并知道了三条高所在直线的交点的位置.
4.2 图形的全等
1.学会辨认全等三角形的对应元素.
2.掌握全等三角形的性质.
自学指导 阅读教材P92~94,完成下列问题.
(一)知识探究
1.能够完全重合的两个图形称为全等图形.如果两个图形全等,它们的形状和大小一定都相同.
2.能够完全重合的两个三角形叫做全等三角形.表示方法:△ABC≌△DEF.
3.全等三角形的性质:全等三角形的对应边相等,对应角相等.
(二)自学反馈
1.下列各组的两个图形属于全等图形的是(
D
)
2.下列关于全等三角形的说法不正确的是(
A
)
A.形状相同的三角形是全等三角形
B.全等三角形的形状相同
C.全等三角形的大小相等
D.全等三角形的对应边相等
只有形状和大小都相等的两个图形才全等,形状相等和大小相等这两个条件缺一不可.
活动1 小组讨论
例 如图,已知△ABC≌△ADE.
(1)写出它们的对应边和对应角;
(2)说明:∠EAC=∠BAD.
解:(1)对应边:AB和AD,AC和AE,BC和DE.
对应角:∠BAC和∠DAE,∠B和∠ADE,∠C和∠E.
(2)因为△ABC≌△ADE,
所以∠CAB=∠EAD.
所以∠CAB-∠CAD=∠EAD-∠CAD,
即∠BAD=∠EAC.
通常把对应顶点的字母写在对应的位置上.
活动2 跟踪训练
1.如图,四边形ABCD与四边形EFGH是全等图形.若AD=5,∠B=70°,则EH=5,∠F=70°.
2.已知△ABC≌△A′B′C′,点A与点A′,点B与点B′是对应点,△A′B′C′的周长为9
cm,AB=3
cm,BC=4
cm,则A′C′=2cm.
3.如图,△BEF≌△AEF,C是BE延长线上的点,ED平分∠AEC,求∠FED的度数.
解:因为△BEF≌△AEF,
所以∠AEF=∠BEF.
因为ED平分∠AEC,
所以∠AED=∠CED.
因为∠AEF+∠BEF+∠AED+∠CED=180°,
所以∠FED=∠AEF+∠AED=90°.
活动3 课堂小结
学生试述:这节课你学到了什么?
4.3 探索三角形全等的条件
第1课时 边边边(SSS)
1.掌握“边边边”证明方法的内容,会运用“边边边”证明方法说明两个三角形全等.
2.能用“边边边”定理判定两个三角形全等和解决相关实际问题,体会三角形的稳定性.
自学指导 阅读教材P97~98,完成下列问题.
(一)知识探究
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”.
(二)自学反馈
1.如图,在△ABC中,AB=AC,EB=EC,则由“SSS”可以直接判定(
B
)
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△BDE≌△CDE
D.以上答案都不对
2.如图,通常凳子腿活动后,木工师傅会在凳腿上斜钉一根木条,这是利用了三角形的稳定性.
活动1 小组讨论
例 如图,已知AB=AC,BE=CE,BD=CD.
(1)图中有几对全等三角形?请分别写出来;
(2)请选择一对全等三角形说明其相等的理由.
解:(1)一共有3对全等三角形,△ABE≌△ACE,△ABD≌△ACD,△BED≌△CED.
(2)因为AB=AC,BE=CE,AE=AE,
所以△ABE≌△ACE(SSS).
注意运用“SSS”说明三角形全等的书写格式,在解答过程中善于挖掘“公共边”这个隐含的条件.
活动2 跟踪训练
1.王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的根数为(
B
)
A.0
B.1
C.2
D.3
2.如图,AB=AD,BC=DC,∠B与∠D相等吗?为什么?
解:∠B=∠D.
理由:连接AC,
在△ABC和△ADC中,
所以△ABC≌△ADC(SSS).
所以∠B=∠D.
三角形全等的判定与性质的应用经常交叉使用.
活动3 课堂小结
1.本节课我们探索得到了三角形全等的条件,发现了证明三角形全等的方法“SSS”.并利用它证明简单的三角形全等问题.
2.添加辅助线构造公共边,可以为证明两个三角形全等提供条件,证明两个三角形全等是证明线段相等或角相等的重要方法.
第2课时 角边角(ASA)与角角边(AAS)
1.掌握三角形全等的“角边角”“角角边”判定方法.
2.学会运用“角边角”“角角边”判定方法进行简单的说理.
自学指导 阅读教材P100~101,完成下列问题.
(一)知识探究
1.两角及其夹边分别相等的两个三角形全等,简写为“角边角”或“ASA”.
2.两角分别相等且其中一组等角的对边相等的两个三角全等,简写为“角角边”或“AAS”.
三角形全等的条件至少需要三对相等的元素(其中至少需要一条边相等).
(二)自学反馈
1.如图,点B,E,F,C在同一直线上,已知∠A=∠D,∠B=∠C,要使△ABF≌△DCE,需要补充的一个条件是答案不唯一,如:AB=DC.(写出一个即可)
2.如图,已知AC平分∠BAD,∠B=∠D.△ABC和△ADC全等吗?请说明理由.
解:△ABC≌△ADC.
理由:因为AC平分∠BAD,
所以∠BAC=∠DAC.
又因为∠B=∠D,AC=AC,
所以△ABC≌△ADC(AAS).
活动1 小组讨论
例1 如图,AB平分∠CAD,∠1=∠2.△AEC和△AED全等吗?试说明理由.
解:△AEC≌△AED.
理由:
因为AB平分∠CAD,
所以∠CAE=∠DAE.
因为∠1=∠2,∠AEC=180°-∠1,∠AED=180°-∠2,
所以∠AEC=∠AED.
又因为AE=AE,
所以△AEC≌△AED(ASA).
应用“ASA”说明三角形全等时注意边是对应角的夹边.
例2 如图,已知,∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?试说明理由.
解:△ABC≌△ADE.
理由:因为∠1=∠2,
所以∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE.
又因为∠C=∠E,AB=AD,
所以△ABC≌△ADE(AAS).
应用“AAS”证三角形全等时应注意边是对应角的对边.
活动2 跟踪训练
1.如图,已知∠ABC=∠DCB,若以“AAS”为依据说明△ABC≌△DCB,还需添加的一个条件是(
A
)
A.∠A=∠D
B.AB=DC
C.∠ACB=∠DBC
D.AC=BD
2.已知:如图,PM=PN,∠M=∠N.试说明:AM=BN.
解:因为∠P=∠P,PM=PN,∠M=∠N,
所以△PBM≌△PAN(ASA).
所以PA=PB.
因为PM=PN,
所以PM-PA=PN-PB,即AM=BN.
善于挖掘隐含条件“公共边、公共角、对顶角”等.
活动3 课堂小结
1.本节内容是已知两个角和一条边对应相等得三角形全等,三个角对应相等不能确定三角形全等.
2.三角形全等的判定和全等三角形的性质常在一起进行综合应用,有时还得反复用两次或两次以上,从而达到解决问题的目的.
第3课时 边角边(SAS)
1.掌握三角形全等的“边角边”判定方法.
2.学会运用“边角边”判定方法进行简单的说理.
自学指导 阅读教材P102~103,完成下列问题.
(一)知识探究
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
(二)自学反馈
1.下列条件能判定两个三角形全等的是(
D
)
A.有两条边对应相等的两个三角形
B.有两边及一角对应相等的两个三角形
C.有三角对应相等的两个三角形
D.有两边及其夹角对应相等的两个三角形
两个三角形具备两边和一对角相等时,不一定全等.
2.如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是(
D
)
A.∠BAC=∠DAC
B.BC=AC
C.∠B=∠D
D.∠ACB=∠ACD
活动1 小组讨论
例 如图,点B为AC的中点,BE=BF,∠1=∠2,△ABE与△CBF全等吗?请说明理由.
解:△ABE≌△CBF.
理由如下:
因为∠1=∠2,
所以∠1+∠EBF=∠2+∠EBF,即∠ABE=∠CBF.
因为B是AC的中点,
所以AB=CB.
又因为BE=BF,
所以△ABE≌△CBF(SAS).
利用“SAS”说明两个三角形全等时,要注意“角”只能是两组相等边的夹角.
活动2 跟踪训练
1.如图,已知AB∥CD,AB=CD,BE=DF,则图中的全等三角形一共有(
A
)
A.3对
B.4对
C.5对
D.6对
2.如图,AD=AE,要根据“SAS”判定△ABD≌△ACE,则还需添加的条件是AB=AC或BE=CD.
分析已知条件,确定说明三角形全等的条件,充分挖掘隐藏条件.
3.如图,在△ABC中,点D为BC上一点,E,F两点分别在边AB,AC上.若BE=CD,BD=CF,∠B=∠C,∠A=50°,求∠EDF的度数.
解:因为在△ABC中,∠A+∠B+∠C=180°,∠B=∠C,∠A=50°,
所以∠B=∠C=(180°-∠A)=65°.
在△BDE和△CFD中,
因为BE=CD,∠B=∠C,BD=CF,
所以△BDE≌△CFD(SAS).
所以∠BDE=∠CFD.
所以∠EDF=180°-(∠BDE+∠CDF)=180°-(∠CFD+∠CDF)=180°-(180°-∠C)=∠C=65°.
活动3 课堂小结
通过本节课的学习,学会利用“SAS”进行说理.
4.4 用尺规作三角形
经过分析与动手操作,掌握已知边、角作三角形的作图方法.
自学指导 阅读教材P105~107,完成下列问题.
(一)知识探究
用尺规作三角形,其实质可以归结为:(1)作一条线段等于已知线段;(2)作一个角等于已知角.
(二)自学反馈
已知三边作三角形,用到的基本作图方法是(
C
)
A.作一个角等于已知角
B.平分一个已知角
C.在射线上截取一线段等于已知线段
D.作一条直线的垂线
活动1 小组讨论
例1 根据下列条件,不能作出唯一的△ABC的是(
A
)
A.AB=3,AC=4,∠B=30°
B.AB=3,BC=4,AC=6
C.∠A=50°,∠B=60°,AB=4
D.AB=3,AC=4,∠A=30°
例2 作图题.(要求:用尺规作图,保留作图痕迹,不写作法)
已知:(如图)线段a和∠α.
求作:△ABC,使AB=AC=a,∠A=∠α.
解:作图如图所示.
尺规作一条线段等于已知线段和作一个角等于已知角是作三角形的基础.
活动2 跟踪训练
1.如图所示,小敏在做题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块空白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是(
C
)
A.SSS
B.SAS
C.ASA
D.AAS
2.如图,已知线段a和∠α,作一个△ABC,使BC=a,AC=2a,∠BCA=∠α.
解:如图,△ABC为所作.
活动3 课堂小结
通过本节课的学习,我们知道了三角形全等条件与作图之间的关系,学会了分析作图题的方法,掌握作图语言的应用.
4.5 利用三角形全等测距离
能利用三角形的全等解决实际问题,体会数学与实际生活的联系.
自学指导 阅读教材P108~109,完成下列问题.
(一)知识探究
(1)全等三角形的性质是全等三角形的对应边相等,对应角相等.
(2)全等三角形的判定方法是SSS,ASA,AAS,SAS.
(二)自学反馈
如图,小牛利用全等三角形的知识测量池塘两端A,B的距离.若△CDO≌△BAO,则只需测出其长度的线段是(
D
)
A.AO
B.CB
C.BO
D.CD
活动1 小组讨论
例1 如图,将两根等长钢条AA′,BB′的中点O连在一起,使AA′,BB′可绕着点O自由转动,就做成了一个测量工具,则AB的长等于容器内径A′B′,那么判定△OAB≌△OA′B′的理由是(
B
)
A.AAS
B.SAS
C.SSS
D.ASA
例2 如图,在一条河的两岸各耸立着一座宝塔,隔河相对,在无任何过河工具情况下,你能测量出两座宝塔间的距离吗?说说你的方法和理由.
解:可以测量出两座宝塔间的距离.
方法:如图所示,把宝塔看作A,B两点,可以沿河岸作射线BF,且使BF⊥AB,在BF上截取BC=CD,过D点作DE⊥BF,使E,C,A在一条直线上,则这两个三角形全等,从而可测量出两座宝塔间的距离.
理由:因为∠ACB=∠ECD,BC=DC,∠B=∠EDC=90°,
所以△ACB≌△ECD(SAS).
所以AB=ED.
活动2 跟踪训练
如图,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示电线杆,BC表示塔松的影长,B′C′表示电线杆的影长,且BC=B′C′,已知电线杆高3
m,则塔松高(
B
)
A.大于3
m
B.等于3
m
C.小于3
m
D.和影子的长相同
活动3 课堂小结
通过本节课的学习我们学会了利用三角形的全等解决实际问题.
三角形
4.1 认识三角形
第1课时 三角形的定义和内角和
1.理解并掌握三角形的概念,会用符号表示三角形.
2.通过剪拼、平移等操作,掌握三角形内角和定理,并能利用三角形内角和定理解决简单问题.
3.能根据三角形内角的大小将三角形分类,并掌握直角三角形的相关性质.
自学指导 阅读教材P81~83,完成下列问题.
(一)知识探究
1.三角形
(1)定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
(2)有关概念:
如图,线段AB,BC,AC是三角形的边,点A,B,C是三角形的顶点,∠A,∠B,∠C是相邻两边组成的角,叫做三角形的内角,简称三角形的角.
(3)表示方法:顶点是A,B,C的三角形,记作“△ABC”,读作“三角形ABC”.
2.三角形三个内角的和等于180°.
3.三角形按角分类:
(1)锐角三角形:三个内角都是锐角;
(2)直角三角形:有一个内角是直角;
(3)钝角三角形:有一个内角是钝角.
4.直角三角形:
如图,我们用符号“Rt△ABC”表示“直角三角形ABC”.把直角所对的边称为直角三角形的斜边,夹直角的两条边称为直角边.直角三角形的两个锐角互余.
(二)自学反馈
1.三角形是(
B
)
A.连接任意三点组成的图形
B.由不在同一直线上的三条线段首尾顺次相接所组成的图形
C.由三条线段组成的图形
D.以上说法均不对
2.如图,△ABC中,∠A=60°,∠B=40°,则∠C等于(
B
)
A.100°
B.80°
C.60°
D.40°
活动1 小组讨论
例1 在△ABC中,∠A的度数是∠B的度数的3倍,∠C比∠B大15°,求∠A,∠B,∠C的度数.
解:设∠B为x°,则∠A为(3x)°,∠C为(x+15)°,从而有
3x+x+(x+15)=180.
解得x=33.
所以3x=99,x+15=48.
答:∠A,∠B,∠C的度数分别为99°,33°,48°.
例2 如图,AC⊥BD,∠1=∠2,∠D=35°,求∠BAD的度数.
解:因为AC⊥BD,
根据“垂直的定义”,
所以∠ACB=∠ACD=90°.
根据直角三角形的两个锐角互余,
所以∠1+∠2=90°.
因为∠1=∠2,
所以∠1=45°.
因为∠D=35°,
根据直角三角形的两个锐角互余.
所以∠CAD=55°.
所以∠BAD=∠1+∠CAD=100°.
“直角三角形的两个锐角互余”常常和三角形内角和定理综合起来求角的度数.
活动2 跟踪训练
1.如图所示是小明用三根火柴组成的图形,其中符合三角形概念的是(
C
)
2.如图,在△ABC中,点D,E分别在边AB,AC上.若∠B+∠C=120°,则∠1+∠2=120°.
3.如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E.
(1)图中有几个直角三角形?是哪几个?
(2)∠A与∠B有什么关系?∠A与∠F呢?
解:(1)4个,分别是△ABC,△CEF,△ADF,△BDE.
(2)∠A+∠B=90°,∠A+∠F=90°.
活动3 课堂小结
本节课我们主要学习了三角形的内角和、三角形按角分类、直角三角形的性质,以及相关的运用.
第2课时 三角形的三边关系
1.会按边对三角形进行分类.
2.通过度量三角形的边长,理解并掌握三角形的三边关系.
自学指导 阅读教材P85~86“随堂练习”之前的内容,完成下列问题.
(一)知识探究
1.三角形按边分类如下:
三角形
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
2.三角形任意两边之和大于第三边,任意两边之差小于第三边.
(二)自学反馈
1.下列说法正确的有(
B
)
①等边三角形是等腰三角形;②三角形的两边之差大于第三边;③三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
A.1个
B.2个
C.3个
D.4个
2.下列长度的三条线段能否组成三角形?为什么?
(1)3,4,8;
解:不能组成三角形,因为3和4的和小于8.
(2)2,5,6;
解:能组成三角形,因为2和5的和大于6,且任意两边的差小于第三边.
(3)5,6,10;
解:能组成三角形,因为5和6的和大于10,且任意两边的差小于第三边.
(4)5,6,11.
解:不能组成三角形,因为5和6的和等于11.
用较短的两条线段之和与最长的线段比较,若和大,则能组成三角形,反之,则不能.
活动1 小组讨论
例1 若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
解:设第三边的长为x,
根据两边之和大于第三边,得x<2+7,即x<9.
根据两边之差小于第三边,得x>7-2,即x>5.
所以x的值大于5小于9.
又因为它是奇数,
所以x只能取7.
例2 用一根长为18厘米的细铁丝围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4厘米的等腰三角形吗?
解:(1)设底边长为x厘米,则腰长为2x厘米.
x+2x+2x=18.
解得x=3.6.
所以三边长分别为3.6厘米,7.2厘米,7.2厘米.
(2)①当4厘米长为底边,设腰长为x厘米,则
4+2x=18.
解得x=7.
所以可围成三边长分别为7厘米、7厘米、4厘米的等腰三角形.
②当4厘米长为腰长,设底边长为x厘米,则
4×2+x=18.解得x=10.
因为4+4<10,
所以此时不能构成三角形.
在不明确给出的边是等腰三角形的腰还是底边时,要分情况进行讨论,同时还要考虑到求出的各边长度能否构成三角形.
活动2 跟踪训练
1.已知△ABC三边a,b,c满足(a-b)2+=0,则△ABC的形状是(
C
)
A.钝角三角形
B.直角三角形
C.等边三角形
D.以上都不对
2.一个等腰三角形的周长为18
cm,一边长为7
cm,求其他两边的长.
解:①若7
cm为腰长,则另一腰长为7
cm,底边长为18-7-7=4(cm),且7
cm,7
cm,4
cm能围成三角形;
②若7
cm为底边长,则腰长为(18-7)÷2=5.5(cm),且7
cm,5.5
cm,5.5
cm也能围成三角形.
故其他两边长分别为7
cm,4
cm或5.5
cm,5.5
cm.
活动3 课堂小结
这节课我们主要学习了:(1)三角形按边分类;(2)三角形的三边关系.第3课时 三角形的中线、角平分线
1.认识三角形的中线、重心、角平分线.
2.能准确画出三角形的中线、角平分线.
自学指导 阅读教材P87~88,完成下列问题.
(一)知识探究
1.在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线.一个三角形共有三条中线,它们都在三角形内部,且交于一点,这点称为三角形的重心.
2.在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.简称三角形的角平分线.一个三角形共有三条角平分线,且交于一点.
(二)自学反馈
1.一个钝角三角形的三条角平分线所在的直线交于一点,这个交点一定在(
A
)
A.三角形内部
B.三角形的一边上
C.三角形外部
D.三角形的某个顶点上
2.填空:
(1)AD是△ABC的角平分线(D在BC所在直线上),那么∠BAD=∠CAD=∠BAC;
(2)AE是△ABC的中线(E在BC所在直线上),那么BE=EC=BC.
活动1 小组讨论
例1 如图,已知△ABC的周长为21
cm,AB=6
cm,BC边上的中线AD=5
cm,△ABD的周长为15
cm,求AC的长.
解:因为AB=6
cm,AD=5
cm,△ABD的周长为15
cm,
所以BD=15-6-5=4(cm).
因为AD是BC边上的中线,
所以BC=8
cm.
因为△ABC的周长为21
cm,
所以AC=21-6-8=7(cm).
例2 如图,在△ABC中,已知∠ABC=80°,∠ACB=40°,BO,CO平分∠ABC,∠ACB,求∠BOC的度数.
解:因为在△ABC中,∠ABC=80°,∠ACB=40°,BO,CO分别平分∠ABC,∠ACB,
所以∠OBC=∠ABC=×80°=40°,∠OCB=∠ACB=×40°=20°.
所以∠BOC=180°-∠OBC-∠OCB=120°.
活动2 跟踪训练
1.如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是(
D
)
A.△DEC中∠C的对边是DE
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.DE是△ABC的中线
2.如图,△ABC中,∠B=90°,AD平分∠BAC,且∠C=4∠BAD,求∠ADC的度数.
解:因为∠B=90°,
所以∠BAC+∠C=90°.
因为AD平分∠BAC,
所以∠BAD=∠CAD.
因为∠C=4∠BAD,
所以2∠BAD+4∠BAD=90°.
所以∠BAD=∠CAD=15°.
所以∠ADC=180°-∠CAD-∠C=180°-15°-60°=105°.
活动3 课堂小结
通过本节课的学习,我们认识三角形的角平分线、中线,并知道了三角形的三条角平分线的交点、三条中线的交点的位置.
第4课时 三角形的高线
1.认识三角形的高线,能画任意三角形的高.
2.了解三角形三条高所在直线交于一点的性质.
自学指导 阅读教材P89~90,完成下列问题.
(一)知识探究
(1)三角形的高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
(2)锐角三角形的三条高在三角形的内部;直角三角形的三条高交于直角顶点处;钝角三角形的三条高所在直线交于一点,此点在三角形的外部.
(二)自学反馈
1.如图,过△ABC的顶点A作BC边上的高,以下作法正确的是(
A
)
回忆并演示“过一点画已知直线的垂线”画法.
2.不一定在三角形内部的是(
C
)
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
活动1 小组讨论
例 如图,在△ABC中,∠BAC=80°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高.
解:(1)因为∠BAC=80°,AE是∠BAC的平分线,
所以∠CAE=40°.
因为AD⊥BC,∠C=60°,
所以∠CAD=30°.
所以∠DAE=10°.
(2)△ABC,△ABE,△AED,△ACD,△ACE,△ABD.
活动2 跟踪训练
1.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是(
C
)
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
2.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
解:(1)因为∠ACB=90°,
所以∠A+∠B=90°.
因为∠1=∠B,
所以∠A+∠1=90°.
所以∠ADC=90°.
所以CD是△ABC的高.
(2)因为∠ACB=90°,AC=8,BC=6,
所以△ABC的面积为24.
因为AB=10,CD是高,
所以CD=4.8.
活动3 课堂小结
通过本节课的学习,我们认识了三角形的高,并知道了三条高所在直线的交点的位置.
4.2 图形的全等
1.学会辨认全等三角形的对应元素.
2.掌握全等三角形的性质.
自学指导 阅读教材P92~94,完成下列问题.
(一)知识探究
1.能够完全重合的两个图形称为全等图形.如果两个图形全等,它们的形状和大小一定都相同.
2.能够完全重合的两个三角形叫做全等三角形.表示方法:△ABC≌△DEF.
3.全等三角形的性质:全等三角形的对应边相等,对应角相等.
(二)自学反馈
1.下列各组的两个图形属于全等图形的是(
D
)
2.下列关于全等三角形的说法不正确的是(
A
)
A.形状相同的三角形是全等三角形
B.全等三角形的形状相同
C.全等三角形的大小相等
D.全等三角形的对应边相等
只有形状和大小都相等的两个图形才全等,形状相等和大小相等这两个条件缺一不可.
活动1 小组讨论
例 如图,已知△ABC≌△ADE.
(1)写出它们的对应边和对应角;
(2)说明:∠EAC=∠BAD.
解:(1)对应边:AB和AD,AC和AE,BC和DE.
对应角:∠BAC和∠DAE,∠B和∠ADE,∠C和∠E.
(2)因为△ABC≌△ADE,
所以∠CAB=∠EAD.
所以∠CAB-∠CAD=∠EAD-∠CAD,
即∠BAD=∠EAC.
通常把对应顶点的字母写在对应的位置上.
活动2 跟踪训练
1.如图,四边形ABCD与四边形EFGH是全等图形.若AD=5,∠B=70°,则EH=5,∠F=70°.
2.已知△ABC≌△A′B′C′,点A与点A′,点B与点B′是对应点,△A′B′C′的周长为9
cm,AB=3
cm,BC=4
cm,则A′C′=2cm.
3.如图,△BEF≌△AEF,C是BE延长线上的点,ED平分∠AEC,求∠FED的度数.
解:因为△BEF≌△AEF,
所以∠AEF=∠BEF.
因为ED平分∠AEC,
所以∠AED=∠CED.
因为∠AEF+∠BEF+∠AED+∠CED=180°,
所以∠FED=∠AEF+∠AED=90°.
活动3 课堂小结
学生试述:这节课你学到了什么?
4.3 探索三角形全等的条件
第1课时 边边边(SSS)
1.掌握“边边边”证明方法的内容,会运用“边边边”证明方法说明两个三角形全等.
2.能用“边边边”定理判定两个三角形全等和解决相关实际问题,体会三角形的稳定性.
自学指导 阅读教材P97~98,完成下列问题.
(一)知识探究
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”.
(二)自学反馈
1.如图,在△ABC中,AB=AC,EB=EC,则由“SSS”可以直接判定(
B
)
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△BDE≌△CDE
D.以上答案都不对
2.如图,通常凳子腿活动后,木工师傅会在凳腿上斜钉一根木条,这是利用了三角形的稳定性.
活动1 小组讨论
例 如图,已知AB=AC,BE=CE,BD=CD.
(1)图中有几对全等三角形?请分别写出来;
(2)请选择一对全等三角形说明其相等的理由.
解:(1)一共有3对全等三角形,△ABE≌△ACE,△ABD≌△ACD,△BED≌△CED.
(2)因为AB=AC,BE=CE,AE=AE,
所以△ABE≌△ACE(SSS).
注意运用“SSS”说明三角形全等的书写格式,在解答过程中善于挖掘“公共边”这个隐含的条件.
活动2 跟踪训练
1.王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的根数为(
B
)
A.0
B.1
C.2
D.3
2.如图,AB=AD,BC=DC,∠B与∠D相等吗?为什么?
解:∠B=∠D.
理由:连接AC,
在△ABC和△ADC中,
所以△ABC≌△ADC(SSS).
所以∠B=∠D.
三角形全等的判定与性质的应用经常交叉使用.
活动3 课堂小结
1.本节课我们探索得到了三角形全等的条件,发现了证明三角形全等的方法“SSS”.并利用它证明简单的三角形全等问题.
2.添加辅助线构造公共边,可以为证明两个三角形全等提供条件,证明两个三角形全等是证明线段相等或角相等的重要方法.
第2课时 角边角(ASA)与角角边(AAS)
1.掌握三角形全等的“角边角”“角角边”判定方法.
2.学会运用“角边角”“角角边”判定方法进行简单的说理.
自学指导 阅读教材P100~101,完成下列问题.
(一)知识探究
1.两角及其夹边分别相等的两个三角形全等,简写为“角边角”或“ASA”.
2.两角分别相等且其中一组等角的对边相等的两个三角全等,简写为“角角边”或“AAS”.
三角形全等的条件至少需要三对相等的元素(其中至少需要一条边相等).
(二)自学反馈
1.如图,点B,E,F,C在同一直线上,已知∠A=∠D,∠B=∠C,要使△ABF≌△DCE,需要补充的一个条件是答案不唯一,如:AB=DC.(写出一个即可)
2.如图,已知AC平分∠BAD,∠B=∠D.△ABC和△ADC全等吗?请说明理由.
解:△ABC≌△ADC.
理由:因为AC平分∠BAD,
所以∠BAC=∠DAC.
又因为∠B=∠D,AC=AC,
所以△ABC≌△ADC(AAS).
活动1 小组讨论
例1 如图,AB平分∠CAD,∠1=∠2.△AEC和△AED全等吗?试说明理由.
解:△AEC≌△AED.
理由:
因为AB平分∠CAD,
所以∠CAE=∠DAE.
因为∠1=∠2,∠AEC=180°-∠1,∠AED=180°-∠2,
所以∠AEC=∠AED.
又因为AE=AE,
所以△AEC≌△AED(ASA).
应用“ASA”说明三角形全等时注意边是对应角的夹边.
例2 如图,已知,∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?试说明理由.
解:△ABC≌△ADE.
理由:因为∠1=∠2,
所以∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE.
又因为∠C=∠E,AB=AD,
所以△ABC≌△ADE(AAS).
应用“AAS”证三角形全等时应注意边是对应角的对边.
活动2 跟踪训练
1.如图,已知∠ABC=∠DCB,若以“AAS”为依据说明△ABC≌△DCB,还需添加的一个条件是(
A
)
A.∠A=∠D
B.AB=DC
C.∠ACB=∠DBC
D.AC=BD
2.已知:如图,PM=PN,∠M=∠N.试说明:AM=BN.
解:因为∠P=∠P,PM=PN,∠M=∠N,
所以△PBM≌△PAN(ASA).
所以PA=PB.
因为PM=PN,
所以PM-PA=PN-PB,即AM=BN.
善于挖掘隐含条件“公共边、公共角、对顶角”等.
活动3 课堂小结
1.本节内容是已知两个角和一条边对应相等得三角形全等,三个角对应相等不能确定三角形全等.
2.三角形全等的判定和全等三角形的性质常在一起进行综合应用,有时还得反复用两次或两次以上,从而达到解决问题的目的.
第3课时 边角边(SAS)
1.掌握三角形全等的“边角边”判定方法.
2.学会运用“边角边”判定方法进行简单的说理.
自学指导 阅读教材P102~103,完成下列问题.
(一)知识探究
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
(二)自学反馈
1.下列条件能判定两个三角形全等的是(
D
)
A.有两条边对应相等的两个三角形
B.有两边及一角对应相等的两个三角形
C.有三角对应相等的两个三角形
D.有两边及其夹角对应相等的两个三角形
两个三角形具备两边和一对角相等时,不一定全等.
2.如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是(
D
)
A.∠BAC=∠DAC
B.BC=AC
C.∠B=∠D
D.∠ACB=∠ACD
活动1 小组讨论
例 如图,点B为AC的中点,BE=BF,∠1=∠2,△ABE与△CBF全等吗?请说明理由.
解:△ABE≌△CBF.
理由如下:
因为∠1=∠2,
所以∠1+∠EBF=∠2+∠EBF,即∠ABE=∠CBF.
因为B是AC的中点,
所以AB=CB.
又因为BE=BF,
所以△ABE≌△CBF(SAS).
利用“SAS”说明两个三角形全等时,要注意“角”只能是两组相等边的夹角.
活动2 跟踪训练
1.如图,已知AB∥CD,AB=CD,BE=DF,则图中的全等三角形一共有(
A
)
A.3对
B.4对
C.5对
D.6对
2.如图,AD=AE,要根据“SAS”判定△ABD≌△ACE,则还需添加的条件是AB=AC或BE=CD.
分析已知条件,确定说明三角形全等的条件,充分挖掘隐藏条件.
3.如图,在△ABC中,点D为BC上一点,E,F两点分别在边AB,AC上.若BE=CD,BD=CF,∠B=∠C,∠A=50°,求∠EDF的度数.
解:因为在△ABC中,∠A+∠B+∠C=180°,∠B=∠C,∠A=50°,
所以∠B=∠C=(180°-∠A)=65°.
在△BDE和△CFD中,
因为BE=CD,∠B=∠C,BD=CF,
所以△BDE≌△CFD(SAS).
所以∠BDE=∠CFD.
所以∠EDF=180°-(∠BDE+∠CDF)=180°-(∠CFD+∠CDF)=180°-(180°-∠C)=∠C=65°.
活动3 课堂小结
通过本节课的学习,学会利用“SAS”进行说理.
4.4 用尺规作三角形
经过分析与动手操作,掌握已知边、角作三角形的作图方法.
自学指导 阅读教材P105~107,完成下列问题.
(一)知识探究
用尺规作三角形,其实质可以归结为:(1)作一条线段等于已知线段;(2)作一个角等于已知角.
(二)自学反馈
已知三边作三角形,用到的基本作图方法是(
C
)
A.作一个角等于已知角
B.平分一个已知角
C.在射线上截取一线段等于已知线段
D.作一条直线的垂线
活动1 小组讨论
例1 根据下列条件,不能作出唯一的△ABC的是(
A
)
A.AB=3,AC=4,∠B=30°
B.AB=3,BC=4,AC=6
C.∠A=50°,∠B=60°,AB=4
D.AB=3,AC=4,∠A=30°
例2 作图题.(要求:用尺规作图,保留作图痕迹,不写作法)
已知:(如图)线段a和∠α.
求作:△ABC,使AB=AC=a,∠A=∠α.
解:作图如图所示.
尺规作一条线段等于已知线段和作一个角等于已知角是作三角形的基础.
活动2 跟踪训练
1.如图所示,小敏在做题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块空白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是(
C
)
A.SSS
B.SAS
C.ASA
D.AAS
2.如图,已知线段a和∠α,作一个△ABC,使BC=a,AC=2a,∠BCA=∠α.
解:如图,△ABC为所作.
活动3 课堂小结
通过本节课的学习,我们知道了三角形全等条件与作图之间的关系,学会了分析作图题的方法,掌握作图语言的应用.
4.5 利用三角形全等测距离
能利用三角形的全等解决实际问题,体会数学与实际生活的联系.
自学指导 阅读教材P108~109,完成下列问题.
(一)知识探究
(1)全等三角形的性质是全等三角形的对应边相等,对应角相等.
(2)全等三角形的判定方法是SSS,ASA,AAS,SAS.
(二)自学反馈
如图,小牛利用全等三角形的知识测量池塘两端A,B的距离.若△CDO≌△BAO,则只需测出其长度的线段是(
D
)
A.AO
B.CB
C.BO
D.CD
活动1 小组讨论
例1 如图,将两根等长钢条AA′,BB′的中点O连在一起,使AA′,BB′可绕着点O自由转动,就做成了一个测量工具,则AB的长等于容器内径A′B′,那么判定△OAB≌△OA′B′的理由是(
B
)
A.AAS
B.SAS
C.SSS
D.ASA
例2 如图,在一条河的两岸各耸立着一座宝塔,隔河相对,在无任何过河工具情况下,你能测量出两座宝塔间的距离吗?说说你的方法和理由.
解:可以测量出两座宝塔间的距离.
方法:如图所示,把宝塔看作A,B两点,可以沿河岸作射线BF,且使BF⊥AB,在BF上截取BC=CD,过D点作DE⊥BF,使E,C,A在一条直线上,则这两个三角形全等,从而可测量出两座宝塔间的距离.
理由:因为∠ACB=∠ECD,BC=DC,∠B=∠EDC=90°,
所以△ACB≌△ECD(SAS).
所以AB=ED.
活动2 跟踪训练
如图,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示电线杆,BC表示塔松的影长,B′C′表示电线杆的影长,且BC=B′C′,已知电线杆高3
m,则塔松高(
B
)
A.大于3
m
B.等于3
m
C.小于3
m
D.和影子的长相同
活动3 课堂小结
通过本节课的学习我们学会了利用三角形的全等解决实际问题.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
