初中数学苏科版九年级上册第二章2.8圆锥的侧面积练习题(word解析版)
文档属性
| 名称 | 初中数学苏科版九年级上册第二章2.8圆锥的侧面积练习题(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 74.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-17 00:00:00 | ||
图片预览




文档简介
初中数学苏科版九年级上册第二章2.7圆锥的侧面积练习题
一、选择题
如图,从一块半径为2m的圆形铁皮上剪出一个半径为的扇形,则此扇形围成的圆锥的侧面积为
A.
B.
C.
D.
一个圆锥的主视图是边长为4cm的正三角形,则这个圆锥的侧面积等于
A.
B.
C.
D.
如图,一只蚂蚁要从圆柱体下底面的A点,沿圆柱表面爬到与A相对的上底面的B点,圆柱底面直径为4,母线为6,则蚂蚁爬行的最短路线长为
A.
B.
C.
D.
用一个圆心角为,半径为6的扇形作一个圆锥的侧面,则这个圆锥的底面半径为
A.
1
B.
2
C.
3
D.
6
如图,圆锥的高,底面半径,则AB的长
A.
大于10
B.
等于10
C.
小于10
D.
不能确定
若圆锥与圆柱的体积和高都相等,则圆锥与圆柱的底面面积的比是
A.
B.
C.
D.
一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数是
A.
B.
C.
D.
已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是
A.
B.
C.
D.
圆锥的底面圆的半径是2cm,母线长是6cm,则该圆锥的侧面展开图的面积是
A.
B.
C.
D.
已知圆锥的母线长为5cm,底面半径为3cm,则该圆锥侧面展开图的圆心角是
A.
B.
C.
D.
二、填空题
若圆锥的母线为5,底面半径为3,则圆锥的侧面积为______.
一个底面半径是3cm的圆锥,其侧面展开图是圆心角为的扇形,则这个圆锥的侧面积为______.
已知扇形的圆心角为,半径等于6,则用该扇形围成的圆锥的底面半径为______.
用半径为4,圆心角为的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为______.
三、解答题
如图,一个圆锥的高为,侧面展开图恰好是半圆.求:
???
圆锥的母线长与底面半径之比;
???
圆锥的侧面积结果保留.
解决下列实际问题.
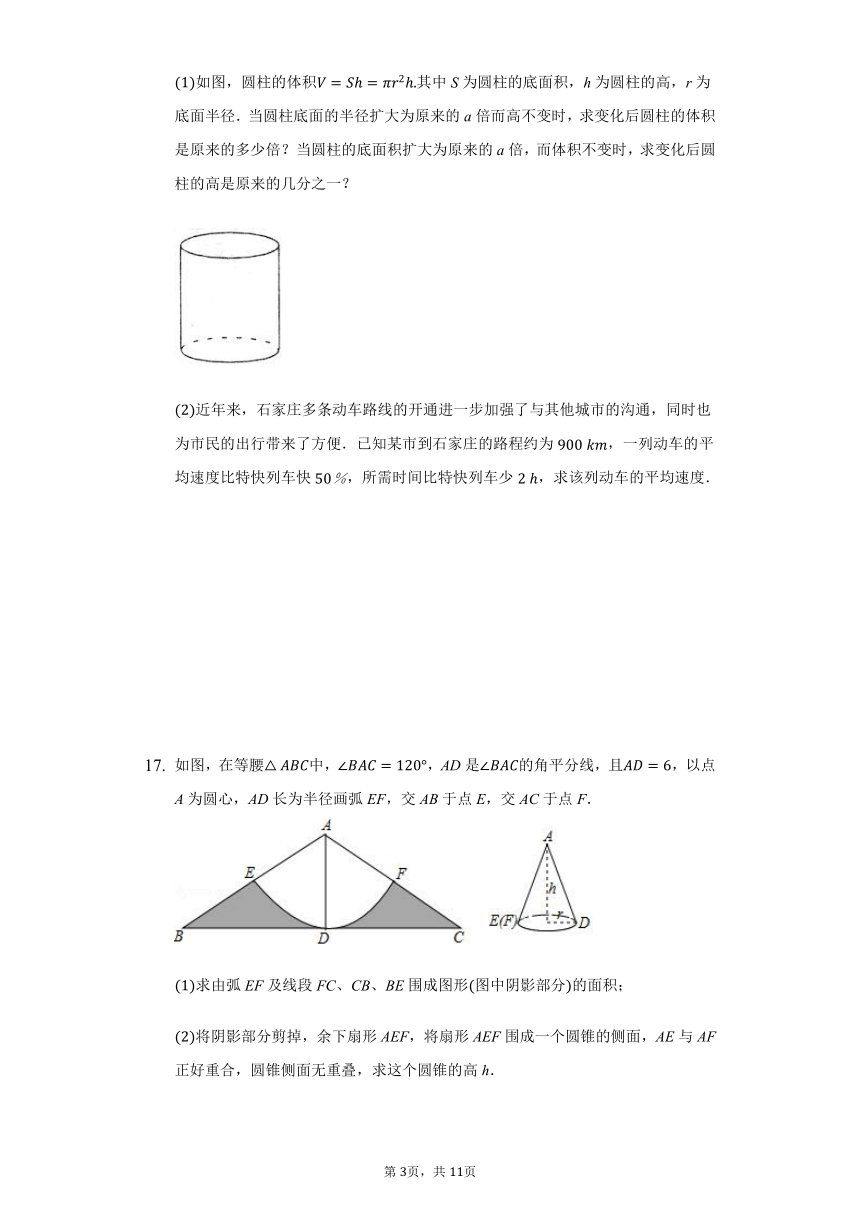
如图,圆柱的体积其中S为圆柱的底面积,h为圆柱的高,r为底面半径.当圆柱底面的半径扩大为原来的a倍而高不变时,求变化后圆柱的体积是原来的多少倍?当圆柱的底面积扩大为原来的a倍,而体积不变时,求变化后圆柱的高是原来的几分之一?
近年来,石家庄多条动车路线的开通进一步加强了与其他城市的沟通,同时也为市民的出行带来了方便.已知某市到石家庄的路程约为,一列动车的平均速度比特快列车快,所需时间比特快列车少,求该列动车的平均速度.
如图,在等腰中,,AD是的角平分线,且,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
求由弧EF及线段FC、CB、BE围成图形图中阴影部分的面积;
将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
答案和解析
1.【答案】A
【解析】解:如图:连接OA,OB,作于点D,
由题意知:,,
所以,
,
,
扇形面积为:,
故选:A.
根据题意求得扇形的圆心角的度数,然后利用扇形面积公式求解即可.
本题考查了圆锥的计算,解题的关键是求得扇形的圆心角,难度不大.
2.【答案】C
【解析】解:根据题意得圆锥的母线长为4,底面圆的半径为2,
所以这个圆锥的侧面积
故选:C.
根据视图的意义得到圆锥的母线长为4,底面圆的半径为2,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
3.【答案】A
【解析】解:把圆柱侧面展开,展开图如图所示,点A,B的最短距离为线段AB的长,
,AC为底面半圆弧长,,
所以.
故选:A.
要求最短路线,首先要把圆柱的侧面展开,利用两点之间线段最短,再利用勾股定理来求.
此题主要考查了平面展开图的最短路径问题,本题的关键是要明确,要求两点间的最短线段,就要把这两点放到一个平面内,即把圆柱的侧面展开再计算.
4.【答案】B
【解析】
【分析】
考查了扇形的弧长公式;圆的周长公式;用到的知识点为:圆锥的弧长等于底面周长.易得扇形的弧长,除以即为圆锥的底面半径.
【解答】
解:扇形的弧长,
圆锥的底面半径为,
故选B.
5.【答案】B
【解析】解:圆锥的高,底面半径,
在中,母线,
故选:B.
直接利用勾股定理求得AB的长即可.
考查了圆锥的计算,解题的关键是了解母线、高及底面半径构成了直角三角形,难度不大.
6.【答案】A
【解析】
【分析】
此题考查了立体图形的认识,圆锥与圆柱的体积计算,掌握圆柱的体积公式与圆锥的体积公式是解题关键,灵活应用公式即可解答.
【解答】
解:设圆锥和圆柱的高是h,体积是V,则:
圆锥的底面积是:,
圆柱的底面积是:,
圆锥的底面积与圆柱的底面积的比为:
,
故答案为:.
7.【答案】B
【解析】解:设母线长为R,底面半径为r,
底面周长,底面面积,侧面面积,
侧面积是底面积的2倍,
,
,
设圆心角为n,
则,
解得,,
故选:B.
根据圆锥的侧面积是底面积的2倍可得到圆锥底面半径和母线长的关系,利用圆锥侧面展开图的弧长底面周长即可得到该圆锥的侧面展开图扇形的圆心角度数.
本题考查的是圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
8.【答案】B
【解析】解:这个圆锥的侧面积
故选:B.
利用圆锥的侧面积公式计算.
本题考查了圆锥的侧面积公式.
9.【答案】C
【解析】解:圆锥的侧面面积.
故选:C.
根据圆锥侧面积底面周长母线长计算.
本题考查圆锥的侧面积表达公式.解题的关键是牢记公式并正确的计算,难度不大.
10.【答案】A
【解析】
【分析】
本题考查的知识点为:弧长圆锥底面周长及弧长与圆心角的关系.解题的关键是熟知圆锥与扇形的相关元素的对应关系.根据弧长圆锥底面周长,圆心角弧长母线长计算.
【解答】
解:,解得.
故选A.
11.【答案】
【解析】解:圆锥的侧面积.
故答案为.
利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
12.【答案】
【解析】解:设圆锥的母线长为lcm,
根据题意得,解得,
所以这个圆锥的侧面积
故答案为.
设圆锥的母线长为lcm,利用弧长公式得到,解得,然后利用扇形的面积公式计算这个圆锥的侧面积.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
13.【答案】2
【解析】解:设该圆锥底面圆的半径为r,
根据题意得,解得,
即该圆锥底面圆的半径为2.
故答案为2
设该圆锥底面圆的半径为rcm,则可根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,然后解方程即可.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
14.【答案】1
【解析】解:设这个圆锥的底面圆半径为r,
根据题意得,
解得,
所以这个圆锥的底面圆半径为1.
故答案为1.
设这个圆锥的底面圆半径为r,利用弧长公式得到,然后解关于r的方程即可.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
15.【答案】解:设圆锥底面半径为rcm,母线为lcm,
由题知?
解得l::1
答:圆锥母线与底面半径之比为2:1;
由题知??,
把代入,解得舍去,,
,
圆锥的侧面积
【解析】本题考查了圆锥的计算,解题的关键是牢记有关的公式.
设出圆锥的底面半径及圆锥的母线长,利用底面周长等于圆锥的弧长得到圆锥的母线与底面的半径之比即可;
首先求得圆锥的底面半径和圆锥的母线长,然后利用圆锥的侧面积的计算方法求得其侧面积即可.
16.【答案】解:当圆柱底面的半径扩大为原来的a倍,则底面积扩大为原来的倍,而高不变时,变化后圆柱的体积是原来的倍;当圆柱的底面积扩大为原来的a倍,而体积不变时,变化后圆柱的高是原来的
解:设特快列车的速度为,则该列动车的平均速度为,
依题意,得:,
解得:,
经检验,是原方程的解,且符合题意,
.
答:该列动车的平均速度为.
【解析】本题考查了圆柱的计算,当圆柱底面的半径扩大为原来的a倍,根据圆的面积半径,可知底面积扩大为原来的倍,而高不变时,根据圆柱的体积底面积高,可知变化后圆柱的体积是原来的倍;当圆柱的底面积扩大为原来的a倍,而体积不变时,根据圆柱的体积底面积高,可知变化后圆柱的高是原来的
本题考查了分式方程的应用,设特快列车的速度为,则该列动车的平均速度为,根据时间路程速度结合行驶900km动车比特快列车少用2小时,即可得出关于x的分式方程,解之经检验后即可得出结论.
17.【答案】解:在等腰中,,
,
是的角平分线,
,,
,
,
由弧EF及线段FC、CB、BE围成图形图中阴影部分的面积;
设圆锥的底面圆的半径为r,
根据题意得,解得,
这个圆锥的高.
【解析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了等腰三角形的性质和扇形的面积公式.
利用等腰三角形的性质得到,,则可计算出,然后利用扇形的面积公式,利用由弧EF及线段FC、CB、BE围成图形图中阴影部分的面积进行计算;
设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,解得,然后利用勾股定理计算这个圆锥的高h.
第2页,共2页
第1页,共1页
一、选择题
如图,从一块半径为2m的圆形铁皮上剪出一个半径为的扇形,则此扇形围成的圆锥的侧面积为
A.
B.
C.
D.
一个圆锥的主视图是边长为4cm的正三角形,则这个圆锥的侧面积等于
A.
B.
C.
D.
如图,一只蚂蚁要从圆柱体下底面的A点,沿圆柱表面爬到与A相对的上底面的B点,圆柱底面直径为4,母线为6,则蚂蚁爬行的最短路线长为
A.
B.
C.
D.
用一个圆心角为,半径为6的扇形作一个圆锥的侧面,则这个圆锥的底面半径为
A.
1
B.
2
C.
3
D.
6
如图,圆锥的高,底面半径,则AB的长
A.
大于10
B.
等于10
C.
小于10
D.
不能确定
若圆锥与圆柱的体积和高都相等,则圆锥与圆柱的底面面积的比是
A.
B.
C.
D.
一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数是
A.
B.
C.
D.
已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是
A.
B.
C.
D.
圆锥的底面圆的半径是2cm,母线长是6cm,则该圆锥的侧面展开图的面积是
A.
B.
C.
D.
已知圆锥的母线长为5cm,底面半径为3cm,则该圆锥侧面展开图的圆心角是
A.
B.
C.
D.
二、填空题
若圆锥的母线为5,底面半径为3,则圆锥的侧面积为______.
一个底面半径是3cm的圆锥,其侧面展开图是圆心角为的扇形,则这个圆锥的侧面积为______.
已知扇形的圆心角为,半径等于6,则用该扇形围成的圆锥的底面半径为______.
用半径为4,圆心角为的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为______.
三、解答题
如图,一个圆锥的高为,侧面展开图恰好是半圆.求:
???
圆锥的母线长与底面半径之比;
???
圆锥的侧面积结果保留.
解决下列实际问题.
如图,圆柱的体积其中S为圆柱的底面积,h为圆柱的高,r为底面半径.当圆柱底面的半径扩大为原来的a倍而高不变时,求变化后圆柱的体积是原来的多少倍?当圆柱的底面积扩大为原来的a倍,而体积不变时,求变化后圆柱的高是原来的几分之一?
近年来,石家庄多条动车路线的开通进一步加强了与其他城市的沟通,同时也为市民的出行带来了方便.已知某市到石家庄的路程约为,一列动车的平均速度比特快列车快,所需时间比特快列车少,求该列动车的平均速度.
如图,在等腰中,,AD是的角平分线,且,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
求由弧EF及线段FC、CB、BE围成图形图中阴影部分的面积;
将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
答案和解析
1.【答案】A
【解析】解:如图:连接OA,OB,作于点D,
由题意知:,,
所以,
,
,
扇形面积为:,
故选:A.
根据题意求得扇形的圆心角的度数,然后利用扇形面积公式求解即可.
本题考查了圆锥的计算,解题的关键是求得扇形的圆心角,难度不大.
2.【答案】C
【解析】解:根据题意得圆锥的母线长为4,底面圆的半径为2,
所以这个圆锥的侧面积
故选:C.
根据视图的意义得到圆锥的母线长为4,底面圆的半径为2,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
3.【答案】A
【解析】解:把圆柱侧面展开,展开图如图所示,点A,B的最短距离为线段AB的长,
,AC为底面半圆弧长,,
所以.
故选:A.
要求最短路线,首先要把圆柱的侧面展开,利用两点之间线段最短,再利用勾股定理来求.
此题主要考查了平面展开图的最短路径问题,本题的关键是要明确,要求两点间的最短线段,就要把这两点放到一个平面内,即把圆柱的侧面展开再计算.
4.【答案】B
【解析】
【分析】
考查了扇形的弧长公式;圆的周长公式;用到的知识点为:圆锥的弧长等于底面周长.易得扇形的弧长,除以即为圆锥的底面半径.
【解答】
解:扇形的弧长,
圆锥的底面半径为,
故选B.
5.【答案】B
【解析】解:圆锥的高,底面半径,
在中,母线,
故选:B.
直接利用勾股定理求得AB的长即可.
考查了圆锥的计算,解题的关键是了解母线、高及底面半径构成了直角三角形,难度不大.
6.【答案】A
【解析】
【分析】
此题考查了立体图形的认识,圆锥与圆柱的体积计算,掌握圆柱的体积公式与圆锥的体积公式是解题关键,灵活应用公式即可解答.
【解答】
解:设圆锥和圆柱的高是h,体积是V,则:
圆锥的底面积是:,
圆柱的底面积是:,
圆锥的底面积与圆柱的底面积的比为:
,
故答案为:.
7.【答案】B
【解析】解:设母线长为R,底面半径为r,
底面周长,底面面积,侧面面积,
侧面积是底面积的2倍,
,
,
设圆心角为n,
则,
解得,,
故选:B.
根据圆锥的侧面积是底面积的2倍可得到圆锥底面半径和母线长的关系,利用圆锥侧面展开图的弧长底面周长即可得到该圆锥的侧面展开图扇形的圆心角度数.
本题考查的是圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
8.【答案】B
【解析】解:这个圆锥的侧面积
故选:B.
利用圆锥的侧面积公式计算.
本题考查了圆锥的侧面积公式.
9.【答案】C
【解析】解:圆锥的侧面面积.
故选:C.
根据圆锥侧面积底面周长母线长计算.
本题考查圆锥的侧面积表达公式.解题的关键是牢记公式并正确的计算,难度不大.
10.【答案】A
【解析】
【分析】
本题考查的知识点为:弧长圆锥底面周长及弧长与圆心角的关系.解题的关键是熟知圆锥与扇形的相关元素的对应关系.根据弧长圆锥底面周长,圆心角弧长母线长计算.
【解答】
解:,解得.
故选A.
11.【答案】
【解析】解:圆锥的侧面积.
故答案为.
利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
12.【答案】
【解析】解:设圆锥的母线长为lcm,
根据题意得,解得,
所以这个圆锥的侧面积
故答案为.
设圆锥的母线长为lcm,利用弧长公式得到,解得,然后利用扇形的面积公式计算这个圆锥的侧面积.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
13.【答案】2
【解析】解:设该圆锥底面圆的半径为r,
根据题意得,解得,
即该圆锥底面圆的半径为2.
故答案为2
设该圆锥底面圆的半径为rcm,则可根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,然后解方程即可.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
14.【答案】1
【解析】解:设这个圆锥的底面圆半径为r,
根据题意得,
解得,
所以这个圆锥的底面圆半径为1.
故答案为1.
设这个圆锥的底面圆半径为r,利用弧长公式得到,然后解关于r的方程即可.
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
15.【答案】解:设圆锥底面半径为rcm,母线为lcm,
由题知?
解得l::1
答:圆锥母线与底面半径之比为2:1;
由题知??,
把代入,解得舍去,,
,
圆锥的侧面积
【解析】本题考查了圆锥的计算,解题的关键是牢记有关的公式.
设出圆锥的底面半径及圆锥的母线长,利用底面周长等于圆锥的弧长得到圆锥的母线与底面的半径之比即可;
首先求得圆锥的底面半径和圆锥的母线长,然后利用圆锥的侧面积的计算方法求得其侧面积即可.
16.【答案】解:当圆柱底面的半径扩大为原来的a倍,则底面积扩大为原来的倍,而高不变时,变化后圆柱的体积是原来的倍;当圆柱的底面积扩大为原来的a倍,而体积不变时,变化后圆柱的高是原来的
解:设特快列车的速度为,则该列动车的平均速度为,
依题意,得:,
解得:,
经检验,是原方程的解,且符合题意,
.
答:该列动车的平均速度为.
【解析】本题考查了圆柱的计算,当圆柱底面的半径扩大为原来的a倍,根据圆的面积半径,可知底面积扩大为原来的倍,而高不变时,根据圆柱的体积底面积高,可知变化后圆柱的体积是原来的倍;当圆柱的底面积扩大为原来的a倍,而体积不变时,根据圆柱的体积底面积高,可知变化后圆柱的高是原来的
本题考查了分式方程的应用,设特快列车的速度为,则该列动车的平均速度为,根据时间路程速度结合行驶900km动车比特快列车少用2小时,即可得出关于x的分式方程,解之经检验后即可得出结论.
17.【答案】解:在等腰中,,
,
是的角平分线,
,,
,
,
由弧EF及线段FC、CB、BE围成图形图中阴影部分的面积;
设圆锥的底面圆的半径为r,
根据题意得,解得,
这个圆锥的高.
【解析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了等腰三角形的性质和扇形的面积公式.
利用等腰三角形的性质得到,,则可计算出,然后利用扇形的面积公式,利用由弧EF及线段FC、CB、BE围成图形图中阴影部分的面积进行计算;
设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,解得,然后利用勾股定理计算这个圆锥的高h.
第2页,共2页
第1页,共1页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
